高斯函数
1 高斯函数积分在无穷区间上积分为1
高斯函数 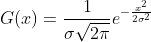 在无穷区间上积分为
在无穷区间上积分为 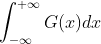 ,
,
为了简便,可先求函数  的积分,证明如下:
的积分,证明如下:
令 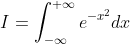 ,则
,则  ,
,
整理得  ,
,
令 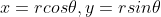 ,使用极坐标变换得
,使用极坐标变换得 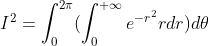 ,
,
先对 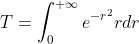 积分,令
积分,令  ,则
,则  ,
,
替换变量得 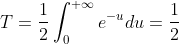
将 T 带入 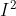 得
得 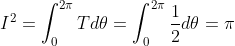 ,
,
因此  。
。
对高斯函数积分表示为  ,
,
令 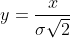 ,
,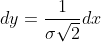 ,
,
使用 y 替换 x 得 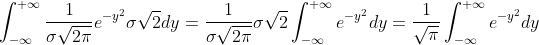 ,
,
由于  ,因此上式值为 1,结论得证。
,因此上式值为 1,结论得证。
2 高斯函数的傅里叶变换仍为高斯函数
令 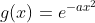 ,其傅里叶变换为
,其傅里叶变换为 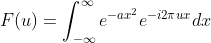 ,
,
令 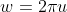 ,带入上式得
,带入上式得 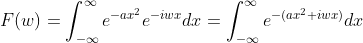 ,
,
将指数部分配方成变量 x 的完全平方和,就可以得到类似  的结构,
的结构,
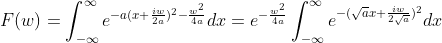 ,
,
令 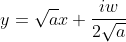 ,
, ,带入上式得
,带入上式得 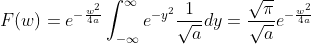 ,
,
由于 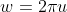 ,有
,有 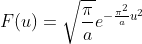 ,
,
令 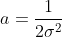 ,有
,有 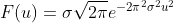 ,
,
由于高斯函数 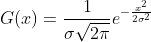 的系数为常数,积分后保持不变,
的系数为常数,积分后保持不变,
因此有 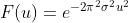 ,其傅里叶变换仍为高斯函数。
,其傅里叶变换仍为高斯函数。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号