采样与混淆
1 冲激信号及其取样特性
定义连续变量 t 在 t = 0 处单位冲激为 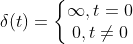 ,且满足
,且满足  。
。
单位冲激信号  在 t = 0 处的值无限大,其积分和为 1。
在 t = 0 处的值无限大,其积分和为 1。
定义连续变量 t 在 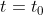 处单位冲激为
处单位冲激为  ,且满足
,且满足  。
。
单位冲激信号  在
在 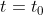 处的值无限大,其积分和为 1。
处的值无限大,其积分和为 1。
设任意连续函数 f(t),对其进行取样操作可表达为  ,由于
,由于  仅在 t = 0 处有非零值,
仅在 t = 0 处有非零值,
取样积分可等价表达为  ,实现在 t = 0 处对 f(t) 采样。
,实现在 t = 0 处对 f(t) 采样。
同理,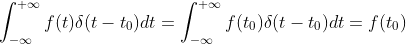 实现在
实现在 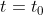 处对
处对  采样。
采样。
对于离散信号,单位冲激与采样定义更加直观,具体如下:
 , 且满足
, 且满足  ,
,
取样特性可表达为 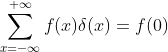 ,
, 。
。
在采样过程中,需要在一定间隔  上进行连续采样,因此,首先定义冲激串信号为
上进行连续采样,因此,首先定义冲激串信号为  ,
,
关于 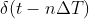 的定义需要详细说明,变量 t,
的定义需要详细说明,变量 t, 为连续变量,但其值定义为 1 !
为连续变量,但其值定义为 1 !
2 冲激信号的傅里叶变换
傅里叶技术描述了有限周期信号的频谱信息,傅里叶变换描述了无限周期信号的频谱信息。
冲激信号  的傅里叶变换为
的傅里叶变换为 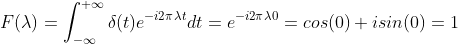 ,
,
因此,单位冲激信号 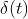 的频谱信息都是 1,即是由所有频谱的余弦波叠加而成。
的频谱信息都是 1,即是由所有频谱的余弦波叠加而成。
冲激信号 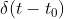 的傅里叶变换为
的傅里叶变换为 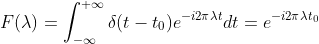 ,
,
通过一些推导,可以得到 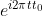 的傅里叶表达式(其中,仅 t 为未知数),具体如下:
的傅里叶表达式(其中,仅 t 为未知数),具体如下:
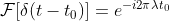 ,
,
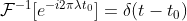 ,
,
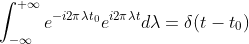 ,
,
 表示对函数
表示对函数  的傅里叶变换,
的傅里叶变换,
令 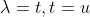 ,通过换元得
,通过换元得 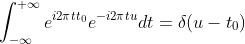 ,换元后 t 表示时间变量,u 表示频率变量,
,换元后 t 表示时间变量,u 表示频率变量,
整理得  ,该结果用于冲激串傅里叶变换中。
,该结果用于冲激串傅里叶变换中。
冲激串  是一个以
是一个以  为周期的周期函数,
为周期的周期函数,
将其表达为傅里叶级数 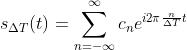 ,
,
傅里叶级数系数为  ,
,
整理得 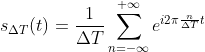 ,
,
由于傅里叶变换是线性运算,因此 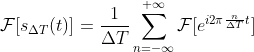 ,
,
已知  ,得
,得  ,
,
因此,周期为  的冲激串的傅里叶变换为周期为
的冲激串的傅里叶变换为周期为 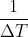 ,幅值为
,幅值为  的冲激串。
的冲激串。
3 卷积的傅里叶变换
函数 f(t) 在卷积核 h(t) 上的卷积为 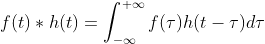 ,
,
对卷积进行傅里叶变换得 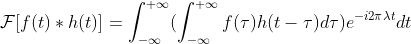 ,
,
令 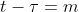 得
得 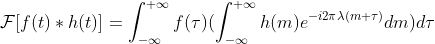 ,
,
整理得  ,
,
因此, 函数 f(t) 在卷积核 h(t) 上的卷积的傅里叶变换等价于分别对函数与卷积核进行傅里叶变换再做乘积运算。
在图像滤波(如高斯滤波)等一些卷积操作中,当卷积核较大时,直接在图像上做卷积操作增加了运算复杂度,
可以将利用卷积的傅里叶变换进行等价操作,从而可节约运算时间。
由于傅里叶变换本身比较耗时,所以在卷积核较小时(如3*3, 5*5, 7*7),直接使用卷积操作会更加迅速。
同理可得, 。
。
4 采样与混淆
以周期  对函数 f(t) 采样可表示为
对函数 f(t) 采样可表示为  ,
,
对采样函数傅里叶变换得 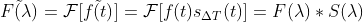 ,
,
已知冲激串的傅里叶变换为  ,
,
将其带入采样函数傅里叶变换得  ,
,
整理得 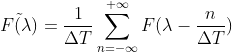 ,
,
取样后傅里叶变换为原函数傅里叶变换的一个无限拷贝,如下图:
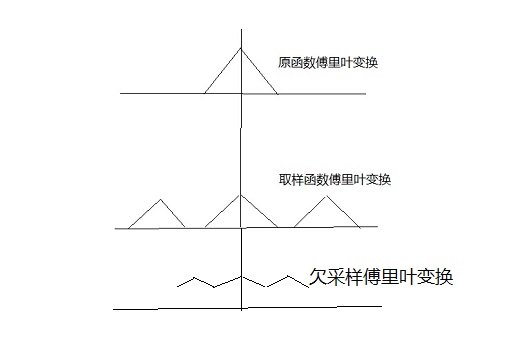
当取样周期为  时,取样函数的傅里叶变换周期为
时,取样函数的傅里叶变换周期为  。
。
当原函数的傅里叶变换仅包含有限频率时,为了从取样函数的傅里叶变换中恢复原函数,必须保证取样函数的傅里叶变换周期大于原函数最大频率的两倍,
即 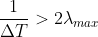 ,即取样周期满足
,即取样周期满足 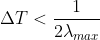 时可以对包含有限频率(带限函数)的函数进行无损失复原,
时可以对包含有限频率(带限函数)的函数进行无损失复原,
当取样周期 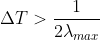 时,取样函数的傅里叶变换存在重叠,在高频部分存在一些混淆,使得无法对原函数进行复原。
时,取样函数的傅里叶变换存在重叠,在高频部分存在一些混淆,使得无法对原函数进行复原。
在对连续图像采样过程中,当采样周期过大会导致高频信号丢失,这是图像混淆的一个原因。
同样的,在对大图像进行缩小操作时,降采样同样对丢失高频信息,从而产生混淆,因此,在降采样前适当模糊图像可以降低混淆。
5 数字图像中混淆无法避免
不论多高的采样频率,数字图像中的混淆总是无法避免的,这是因为数字图像是有限时间信号,而有限时间信号包含无限频率,
所以无法从采样函数的傅里叶变换中分离出一个完整的原函数的傅里叶变换。
比如,单位冲激信号是一个有限时间信号,其傅里叶变换为所有频率均为 1 的函数,故单位冲激信号不是带限的。
下面对一个简单的有限信号进行傅里叶变换

原函数为  ,
,
对其进行傅里叶变换为 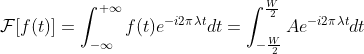 ,
,
整理得 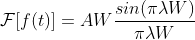 ,因此有限信号不是带限的,数字图像采样过程中必然引入混淆。
,因此有限信号不是带限的,数字图像采样过程中必然引入混淆。
参考资料 Digital Image Processing Rafael C. Gonzalez & Richard E. Woods
Signals and Systems Alan V. Oppenheim & Alan S. Willsky
A First Course in Wavelets with Fourier Analysis Albert Boggess & Francis J. Narcowich



 浙公网安备 33010602011771号
浙公网安备 33010602011771号