图像配准
对于两幅不同角度拍摄图像,不考虑光学成像相关信息,仅认为两幅图像是通过某一种平面映射(如仿射变换)相关联。使用该模型对两幅图像配准方法如下:
1 特征检测与匹配
1)使用任意特征点检测算法分别检测出两幅图像上得显著特征点(如 Harris 角点,SIFT,SURF等);
2)使用特征点描述算法对两幅图像特征点生成具体描述信息(如 BRIEF,SIFT, SURF等);
3)使用特征点匹配算法对两幅图像特征点进行匹配(如 Brute force matching,Fast approximate nearest neighbors matching);
4)保留部分特征点匹配度较高匹配点,作为图像配准基本输入信息;
2 二维几何变换
1)平移(translation)
设 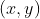 为变换前坐标,
为变换前坐标,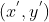 为变换后坐标,
为变换后坐标,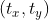 为平移向量,平移变换可表示为
为平移向量,平移变换可表示为 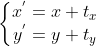 ,
,
使用矩阵表示为 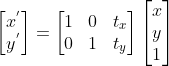 ,令
,令 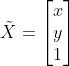 ,
, ,
, ,
,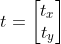 ,
,
其中 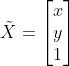 为齐次坐标表达,平移变换可简化为
为齐次坐标表达,平移变换可简化为  ;
;
2)平移+旋转(rotation)
在平移基础上加入旋转被称为刚体运动(rigid body motion)或者欧几里得变换(euclidean transformation),该变换前后欧式距离保持不变;
而单独平移变换不仅欧式距离保持不变,同时线条方向等均保持不变。
向量 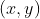 绕原点旋转
绕原点旋转 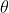 后为
后为 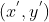 ,以下给出两者之间的关系:
,以下给出两者之间的关系:

如上图所示,有 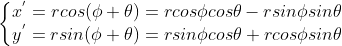 ,
,
将 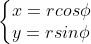 带入得
带入得 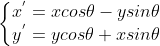 ,得到了向量
,得到了向量 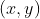 绕原点旋转
绕原点旋转 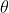 后的表达式。
后的表达式。
添加平移分量得  ,使用矩阵表示为
,使用矩阵表示为 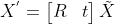 ,其中
,其中 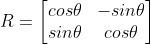 。
。
3)相似变换(similarity transform)
在平移与旋转基础上添加缩放变换则构成了相似变换,相似变换使得变换前后点间距离发生变化,但保持角度不变。
相似变换可表达为 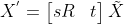 。
。
4)仿射变换(affine transform)
放射变换不改变平行性质,但不再保持角度不变,可表示为 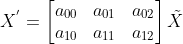 。
。
5)透视变换(perspective transform)
透视变换不再保持平行性质,但保持直线性质。透视变换需要使用齐次坐标表示为  ,
,
变换后转换为非齐次坐标为 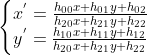 。
。
3 图像配准
假设两幅图像特征点之间存在以上以上5种变换关系中任意一种变换 A,变换前后可表示为  。
。
由于已知点对集 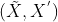 ,可以通过重新改写表达式求解 A,改写如下:
,可以通过重新改写表达式求解 A,改写如下:
将矩阵 A 改写为列向量 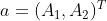 ,构造矩阵
,构造矩阵 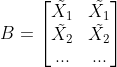 ,构造向量
,构造向量 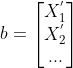 ,
,
变换  可被改写为
可被改写为  ,其中 a 为未知量,使用最小二乘法求解线性方程组可以得到最佳变换矩阵 A。
,其中 a 为未知量,使用最小二乘法求解线性方程组可以得到最佳变换矩阵 A。
如何两幅图像特征点之间得变换为仿射变换,使用以上方案求解最佳变换矩阵是合理的;但如果两幅图像间变换为相似变换或者刚体变换,以上方案则存在参数冗余。
下面首先来分析各种变换的参数情况:
1)平移变换仅依赖平移向量 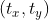 ,故其参数为
,故其参数为 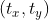 ,观察公式
,观察公式 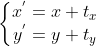 可知平移变换为线性变换。
可知平移变换为线性变换。
2)刚体变换在依赖平移向量基础上增加了旋转角度 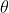 ,故其参数为
,故其参数为 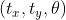 ;观察公式
;观察公式  可知,
可知,
刚体变换不是线性变换;若将参数修改 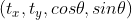 ,可以认为该变换是关于变量
,可以认为该变换是关于变量 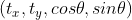 的线性变换。
的线性变换。
3)相似变换依赖参数可表示为 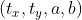 ,其变换矩阵可改写为
,其变换矩阵可改写为 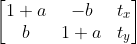 ,该变换是关于变量
,该变换是关于变量 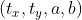 的线性变换。
的线性变换。
这里使用 1 + a 而不使用 a,是因为当该参数无变换时,该变换矩阵为单位矩阵!
4)仿射变换变换矩阵可表示为 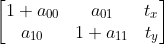 ,其依赖参数为
,其依赖参数为 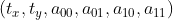 ,该变换为线性变换。
,该变换为线性变换。
5)透视变换矩阵可表示为 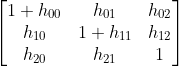 ,其依赖参数为
,其依赖参数为  ,观察公式
,观察公式 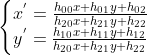 可知该变换为非线性变换。
可知该变换为非线性变换。
使用变换参数 p,两幅图像间特征点变换关系可表达为  , 其中
, 其中 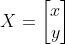 ,
,  ;变换后向量与匹配向量平方和最小化即为最优解,表达如下:
;变换后向量与匹配向量平方和最小化即为最优解,表达如下:
 ,
,
对于平移,刚体(使用参数 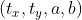 ),相似及仿射变换,
),相似及仿射变换, 为线性变换函数,下面以相似变换为例给出推导:
为线性变换函数,下面以相似变换为例给出推导:
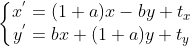 , 当输入向量
, 当输入向量 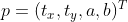 改变
改变 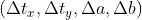 时,利用线性近似可得:
时,利用线性近似可得:
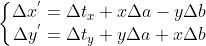 ,写成矩阵为
,写成矩阵为 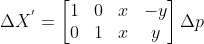 ,
,
其中 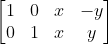 为变换矩阵
为变换矩阵 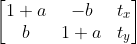 关于变量
关于变量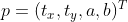 的雅可比矩阵。
的雅可比矩阵。
当变量 p 从 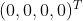 增加到
增加到  ,输入值
,输入值 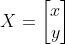 增加到
增加到  ,
,
得 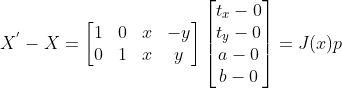 ,因此
,因此  描述了点对间得运动关系。
描述了点对间得运动关系。
 所描述的点对间的运动与实际点对间的运动差越小则表示变换模型越合理,因此,最小化平方和可改写为:
所描述的点对间的运动与实际点对间的运动差越小则表示变换模型越合理,因此,最小化平方和可改写为:
 ,公式中仅 p 为未知量,展开公式如下:
,公式中仅 p 为未知量,展开公式如下:
 ,
,
使 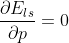 即可求得最小平方和,得到线性方程组
即可求得最小平方和,得到线性方程组  ,可求解 p。
,可求解 p。
4 非线性变换
由于受到镜头畸变以及成像角度影响,匹配点间的变换关系一般都无法使用简单线性关系表示,可以首先利用简单线性变换求得一个初始变换参数,
然后根据初始变换参数使用迭代方法求得精确变换关系。
在二维几何变换中,刚体变换参数为 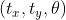 时为非线性变换。使用参数
时为非线性变换。使用参数 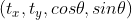 或
或 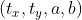 可将该变换视为线性变换,
可将该变换视为线性变换,
由于满足  ,所以参数 a,b 并非独立参数,线性变换求解的结果也不一定满足关系
,所以参数 a,b 并非独立参数,线性变换求解的结果也不一定满足关系 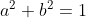 ,
,
但可以将线性变换结果作为初始参数值  ,将其转换为非线性参数
,将其转换为非线性参数 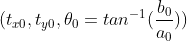 ,
,
使用迭代算法(Levenberg Marquardt)即可求得最优解。具体如下:
1)第一次迭代前,参数 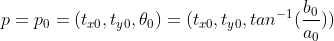 ,该值为线性变换的结果;
,该值为线性变换的结果;
2)使用初始值求解更精确的变换参数 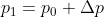 ,根据线性近似有
,根据线性近似有  ,
,
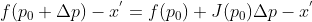 ,由于
,由于 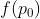 已知,为 x 经过参数
已知,为 x 经过参数  线性变换的结果,
线性变换的结果,
令  ,进一步改写为
,进一步改写为 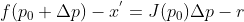 ,
,
对于所有匹配点,最小化 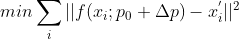 即为一次更好的迭代结果,
即为一次更好的迭代结果,
展开公式得 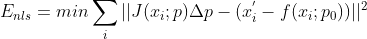 , 其中
, 其中 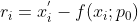 线性变换与匹配点直接的差值向量,
线性变换与匹配点直接的差值向量,
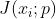 为变换参数 p 在
为变换参数 p 在 ![]() 点的雅可比矩阵,以上量均为已知量;
点的雅可比矩阵,以上量均为已知量;
进一步整理 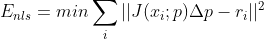 ,该函数的未知量为
,该函数的未知量为  ,最小化函数可转换为求解如下线性方程组:
,最小化函数可转换为求解如下线性方程组:
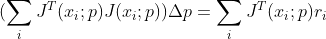 ,同时可估计本次迭代后误差值;
,同时可估计本次迭代后误差值;
3)使用 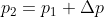 进行第二次迭代,其中
进行第二次迭代,其中  为第一次迭代的结果,
为第一次迭代的结果,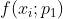 为
为 ![]() 点经过
点经过  变换后的结果,重复 2)即可得到下一个迭代值,
变换后的结果,重复 2)即可得到下一个迭代值,
估计第二次迭代后变换误差值,比较相邻两次迭代的变换误差可知是否得到一个更好的收敛值,同时也可以根据变换误差值决定何时终止迭代。
参考资料 Computer Vision: Algorithms and Applications Richard Szeliski
Computer Graphics with OpenGL Donald Hearn & M. Pauline Baker & Warren R. Carithers



 浙公网安备 33010602011771号
浙公网安备 33010602011771号