数学小知识点
超平面
超平面定义为: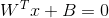 ,对向量W归一化得:
,对向量W归一化得: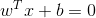 ,其中,
,其中,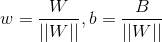 ,归一化处理可简化后续一些计算。
,归一化处理可简化后续一些计算。
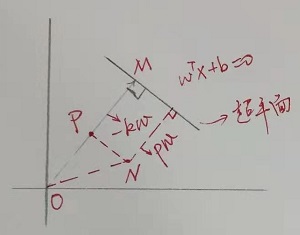
超平面单位法向量为w,证明如下:
设  为超平面上得点,则有:
为超平面上得点,则有: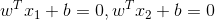 ,
,
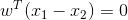 ,向量w与超平面上任意方向线段垂直,则w为超平面单位法向量。
,向量w与超平面上任意方向线段垂直,则w为超平面单位法向量。
原点到超平面距离为b,证明如下:
过原点O作到超平面距离垂线,设OM=-kw,代入超平面得: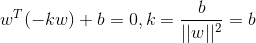 ,
,
则原点O到超超平面距离为 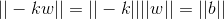 。
。
任意点N到超平面距离为 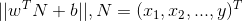 ,证明如下:
,证明如下:
点N在OM上投影向量为: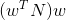 ,任意点N到超平面作垂线向量为:
,任意点N到超平面作垂线向量为: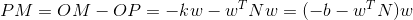 ,则距离为:
,则距离为: 。
。
矩阵微分
1)y=Ax, y为m*1向量,x为n*1向量,A为m*n矩阵,A不依赖x,则有  ,证明如下:
,证明如下:
 ,
,  。
。
2)y=Ax, y为m*1向量,x为n*1向量,A为m*n矩阵,A不依赖x,x=f(z),根据链式法则有 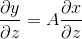 。
。
3) ,y为m*1向量,x为n*1向量,A为m*n矩阵,A不依赖xy,则有
,y为m*1向量,x为n*1向量,A为m*n矩阵,A不依赖xy,则有 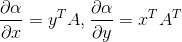 ,证明如下:
,证明如下:
令 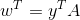 ,通过变换得:
,通过变换得: 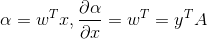 。
。
令  ,则有:
,则有: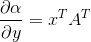 。
。
4) ,x为n*1向量,A为n*n矩阵,A不依赖x,则有
,x为n*1向量,A为n*n矩阵,A不依赖x,则有  ,证明如下:
,证明如下:
 ,
,  ,
,
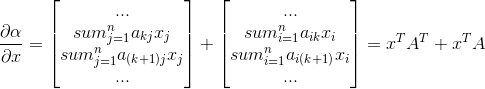 ,结论得证。
,结论得证。
5) ,x为n*1向量,A为n*n对称矩阵矩阵,A不依赖x,由于
,x为n*1向量,A为n*n对称矩阵矩阵,A不依赖x,由于 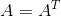 ,则有
,则有 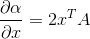 。
。
6)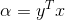 ,y为n*1向量,x为n*1向量,x与y均依赖于z,根据链式法则有
,y为n*1向量,x为n*1向量,x与y均依赖于z,根据链式法则有 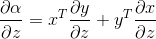 ,若x=y,则有
,若x=y,则有  。
。
7) ,y为m*1向量,x为n*1向量,A为m*n矩阵,A不依赖xy,x与y均依赖于z,根据链式法则有
,y为m*1向量,x为n*1向量,A为m*n矩阵,A不依赖xy,x与y均依赖于z,根据链式法则有  。
。
8) ,x为n*1向量,A为n*n矩阵,A不依赖x,x依赖于z,根据链式法则有
,x为n*1向量,A为n*n矩阵,A不依赖x,x依赖于z,根据链式法则有  。
。
9)A为n*n矩阵,A的各项为变量  函数,定义
函数,定义  ,则有
,则有  ,证明如下:
,证明如下:
由于 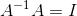 ,左右微分得:
,左右微分得: ,
,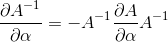 。
。
曲率
曲率定义为单位弧段上切线旋转过的角度, 。针对直线情况,K=0表示直线无弯曲;针对圆形,
。针对直线情况,K=0表示直线无弯曲;针对圆形, 表示圆形弯曲程度与半径呈反比。
表示圆形弯曲程度与半径呈反比。
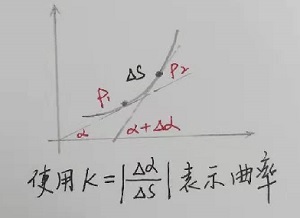
在直角坐标系下,设曲线方程为 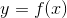 ,且函数具有二阶导数,欲求曲线上某一固定点(x, f(x)) 的曲率,有如下推导:
,且函数具有二阶导数,欲求曲线上某一固定点(x, f(x)) 的曲率,有如下推导:
根据导数定义可知 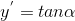 ,使用反函数重写得
,使用反函数重写得  ,两边对 x 求导得
,两边对 x 求导得  ,
,
代入 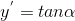 得
得  ,到此,建立起了
,到此,建立起了  与
与  关系,根据弧微分公式可建立
关系,根据弧微分公式可建立  与
与 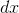 关系,如下:
关系,如下:
极限情况下,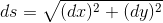 ,而
,而 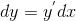 ,则有
,则有 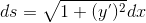 。
。
根据以上关系,可建立 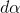 与
与 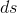 关系:
关系: 。
。
当曲线表示为参数方程 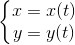 时,可以首先求出 y 对 x 的一阶与二阶导数,代入之前曲率公式即可。
时,可以首先求出 y 对 x 的一阶与二阶导数,代入之前曲率公式即可。
使用反函数关系,可求得一阶导数为 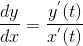 ,由于一阶导数是关于 t 的函数,则二阶导数定义为
,由于一阶导数是关于 t 的函数,则二阶导数定义为  ,
,
根据基本求导法则得 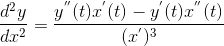 。
。
向量范数与矩阵范数
在实数空间R中,可以很方便比较两个数的大小关系。而针对两个n维向量 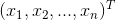 ,
, ,如果需要比较大小关系,需要定义一个准则,如到原点距离(即欧氏距离)。而范数即为不同的准则,如
,如果需要比较大小关系,需要定义一个准则,如到原点距离(即欧氏距离)。而范数即为不同的准则,如  等,其公式为:
等,其公式为: 。
。
当k=2时,即为常见的欧式距离;当k=1时,为向量中各元素绝对值之和;当k=0时,表示向量中非零元素个数;当 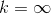 时,表示向量中绝对值最大元素绝对值。
时,表示向量中绝对值最大元素绝对值。
针对 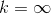 时,可以使用极限求解,有
时,可以使用极限求解,有  。
。
将矩阵作用于向量(矩阵左乘向量),表示矩阵对向量进行线性变换。如果矩阵为单位矩阵,则变换后向量于变换前保持一致。如果矩阵非单位向量,变换后向量与变换前则存在差异,不同矩阵对向量的变换的差异不一致,这里使用矩阵范数表示这种变换的最大差异。显然,要度量变换前后向量差异,需要选择合适的度量准则,即以上所述的向量范数。
在选择了合适的向量范数后,对应的矩阵范数表示该度量规则下矩阵变换前后的最大差异,则有:
1)使用矩阵每列绝对值之和的最大值表示矩阵A的 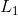 范数;
范数;
2)使用矩阵每行绝对值之和的最大值表示矩阵A的  范数;
范数;
3)使用 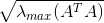 (矩阵
(矩阵  最大特征值开平方)表示矩阵A的
最大特征值开平方)表示矩阵A的  范数。
范数。
椭圆
标准椭圆解析方程为 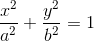 , a, b表示椭圆在xy方向上的半轴长度。
, a, b表示椭圆在xy方向上的半轴长度。
将标准椭圆旋转 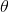 弧度后,相当于对当前坐标下图形上所有点旋转
弧度后,相当于对当前坐标下图形上所有点旋转 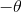 弧度后满足标准方程,则有
弧度后满足标准方程,则有  。
。
从原点构建一条射线 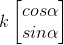 ,射线与旋转
,射线与旋转  弧度后椭圆相交于一点,如何求该点坐标,方法如下:
弧度后椭圆相交于一点,如何求该点坐标,方法如下:
1)旋转坐标系 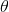 弧度,在该坐标系下椭圆为标准椭圆;
弧度,在该坐标系下椭圆为标准椭圆;
2)原射线在新坐标系下表示为  , 在该射线上存在一点满足标准椭圆方程
, 在该射线上存在一点满足标准椭圆方程  ,求解出新坐标系下交点坐标;
,求解出新坐标系下交点坐标;
3)将求解出交点坐标旋转 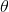 弧度即得到交点坐标。
弧度即得到交点坐标。
分部积分法
求解积分  ,可使用分部积分法,具体思路如下:
,可使用分部积分法,具体思路如下:
1)根据积分乘法法则:  ,可做如下变形:
,可做如下变形: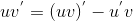 ;
;
2)两边积分得:  ,
, 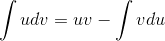 ;
;
3)令 u = x, dv = sinxdx,代入以上公式可得:  ;
;
4)解以上积分可得:  。
。
空间直线
在 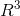 中,直线方程可表示为
中,直线方程可表示为  。例如:
。例如: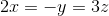 表示一条三维空间直线,可使用参数方程改写:
表示一条三维空间直线,可使用参数方程改写:
令 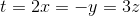 ,有:
,有:
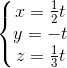 , 直线方向向量为:
, 直线方向向量为: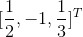 。
。
逆矩阵求解
如果矩阵(方阵) A 存在逆矩阵,则等式  成立,可以使用 Gauss-Jordan Method 求逆矩阵,主要思路为对长方矩阵
成立,可以使用 Gauss-Jordan Method 求逆矩阵,主要思路为对长方矩阵  进行消元法处理,当矩阵 A 经过消元后得到 I,矩阵 I 则变成了
进行消元法处理,当矩阵 A 经过消元后得到 I,矩阵 I 则变成了  。证明如下:
。证明如下:
1)对 A 消元过程可描述为 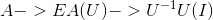 ;
;
2)使用同样的消元矩阵作用于 I 可描述为: ,结论得证。
,结论得证。
使用 Gauss-Jordan Method 求逆矩阵时,对矩阵 A 消元到 U 时并不停止消元,还需要继续对 U 消元,直到 U 变成对角矩阵,然后将对角矩阵化为单位矩阵。该过程同样作用于右边矩阵 I ,故 Gauss-Jordan Method 计算量较大,但逻辑简单明了,适合小矩阵时手动演算。更简单的方法是使用矩阵LU分解 + 多次回带即可求得逆矩阵。思路如下(假设3*3方阵):
1)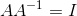 可被改写为:
可被改写为:  ,其中,
,其中,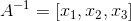 ,
,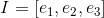 ;
;
2)拆分以上等式为三个线性方程组: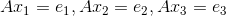 ;
;
3)观察以上三个线性方程组,其中, 为矩阵
为矩阵 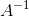 的列组成,其系数矩阵都为 A ,故仅需要一次LU分解,然后通过回带分别求解
的列组成,其系数矩阵都为 A ,故仅需要一次LU分解,然后通过回带分别求解  即可。
即可。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号