数据结构之树状数组(算法知识总结)
\(\Huge{数据结构之树状数组(算法知识总结)}\)
介绍
树状数组顾名思义,本质就是一个数组,但是其储存结构与一般的线性数组不同。如果我们使用常规的数组进行单点修改与区间查询时,其时间复杂度分别是\(O(1)\)和\(O(n)\),当问题中涉及到的区间查询较多时,时间复杂度会叠的很高。这时就可以使用树状数组来解决这种单点修改、区间修改、单点查询、区间查询的问题。
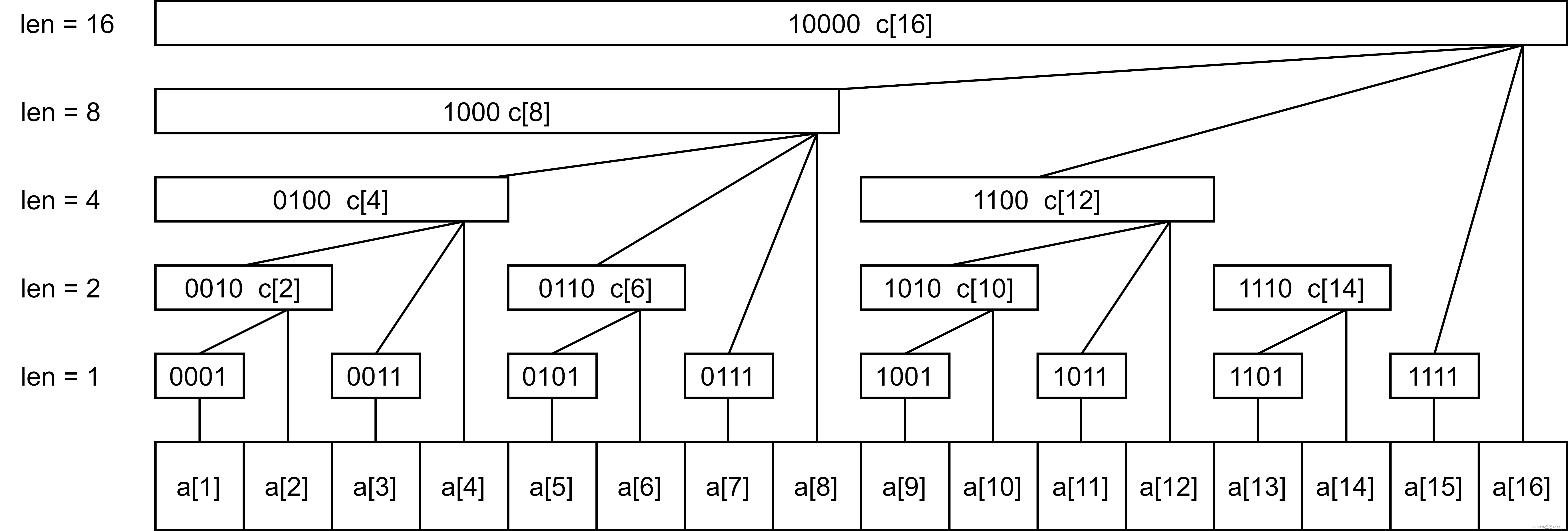
树状数组的结构图如下图所示,下图的结构是如何来实现的呢?
树状数组与二进制的联系紧密,我们知道:任何一个正整数都可以被二进制分解,即可以由若干个2的不重复整次幂数相加得到(唯一分解性质)。若一个正整数\(x\)的二进制表示为:\(a_{k-1}、a_{k-2}...、a_1、a_0\),其中等于1的位是{\(a_{i_1},a_{i_2}...,a_{i_m}\)},则该正整数可以被二进制分解为:$$x=2{i_1}+2+...+2^{i_m}$$
我们设\(i_1>i_2>...>i_m\),进一步的区间\([1,x]\)可以分成\(O(logx)\)个小区间:
- 长度为\(2^{i_1}\)的小区间\([1,2^{i_1}]\)
- 长度为\(2^{i_2}\)的小区间\([2^{i_1}+1,2^{i_1}+2^{i_2}]\)
- 长度为\(2^{i_3}\)的小区间\([2^{i_1}+2^{i_2}+1,2^{i_1}+2^{i_2}+2^{i_3}]\)
......
m. 长度为\(2^{i_m}\)的小区间\([2^{i_1}+2^{i_2}+2^{i_3}+...+2^{i_{m-1}}+1,2^{i_1}+2^{i_2}+2^{i_3}+...+2^{i_{m}}]\)
这些小区间的共同特点是:若区间结尾为R,则区间长度就为R的二进制分解下最小的2的次幂,即\(lowbit(R)\)。例如\(6=0110=2^2+2^1\)
则\(lowbit(6)\)为2。一定结合下图理解
所以:
\(c[8]=c[4]+c[6]+c[7]+a[8]\)
\(c[6]=c[5]+a[6]\)
\(c[5]=a[5]\)
如何计算lowbit(x)
#define lowbit(x) (x & -x)
区间查询
区间查询过程中,该函数功能是查询前x项的前缀和,每次x减去它的最小的二次幂,然后相加,sum即为前x项的和。
若要实现任意区间查询,只需像前缀和数组求区间和一样,ask[x]-ask[y]。
int ask(int x) {
int sum = 0;
for(; x; x -= lowbit(x)) sum += c[x];
return sum;
}
单点增加
树状数组实现单点增加需调用下列函数,函数的意义就是向上遍历将它上面连接的数组都加上val。
void add(int x, int val) {
for(; x <= n; x += lowbit(x)) c[x] += val;
}
单点查询+区间修改
树状数组只能进行单点修改+区间查询的操作,我们可以利用差分思想将区间修改+单点查询的操作转换成单点修改+区间查询。定义差分数组b[i] = a[i] - a[i-1],那么\(a[i]=a[i]+\sum_{j=1}^{i}b[j]\) ,即a[i]其实就是数组b的1到 i 的前缀和,这样就把\(a[i]\) 的单点查询变成了\(b[i]\)的区间查询。对于a数组的区间修改,如果要将\(a[x]\)到\(a[y]\)的值都+val,那么只要进行b[x] + val , b[y+1] - val即可,这样就把区间修改变成了单点修改。
例题:AcWing 242. 一个简单的整数问题
//AcWing 242. 一个简单的整数问题
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x & -x)
#define endl '\n'
typedef pair<int, int> pir;
const int mod = 1e9 + 10;
const int N = 1e5 + 10;
int n, m, a[N];
int tr[N];
void add(int x, int c) {
for(int i = x; i <= n; i += lowbit(i)) {
tr[i] += c;
}
}
int ask(int x) {
int sum = a[x];
for(; x; x -= lowbit(x)) sum += tr[x];
return sum;
}
int main(void){
IOS
cin >> n >> m;
for(int i = 1; i <= n; i ++ ) {
cin >> a[i];
}
while(m -- ) {
string s; cin >> s;
if(s == "C") {
int l, r, d; cin >> l >> r >> d;
add(l, d); add(r + 1, - d);
} else {
int x; cin >> x;
cout << ask(x) << endl;
}
}
return 0;
}
区间查询+区间修改
在上一种情况中,我们用树状数组维护了一个数组b,对于每一次修改,我们都将b数组看做差分数组进行处理。那么进行区间查询时,也就是求a数组前x项的前缀和时该如何处理?
数组a的前缀和:$$\sum_{i=1}^{x} \sum_{j=1}{i}b[j]=\sum_{i=1} (x-i+1)\times b[i]=(x+1)\sum_{i=1}^{x}b[i] -\sum_{i=1}^{x}i\times b[i] $$
用图片直观理解上述公式
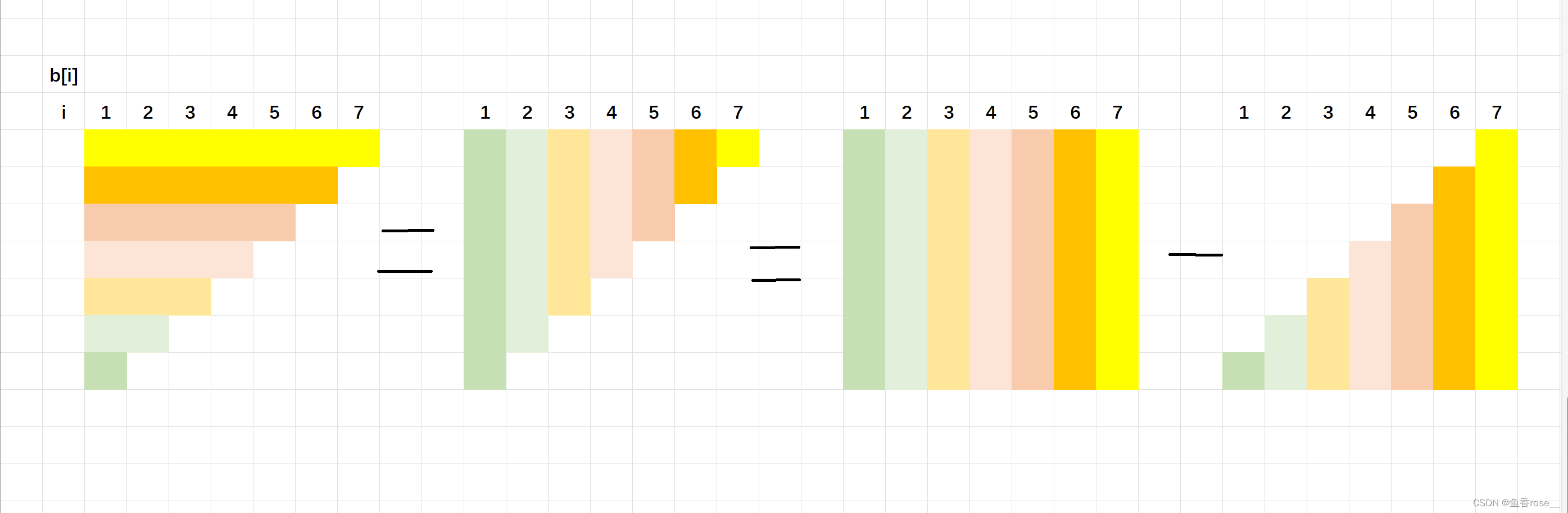
在本问题中,需要增加一个树状数组,用于维护i*b[i]的前缀和。
具体来说,我们建立两个树状数组\(c_0\)和\(c_1\),起初全部赋值为0.对于每次区间修改,我们共执行4个操作:
- 树状数组\(c_0\)中,把位置\(l\)上的数加\(d\)。
- 树状数组\(c_0\)中,把位置\(r+1\)上的数减\(d\)。
- 树状数组\(c_1\)中,把位置\(l\)上的数加\(l*d\)。
- 树状数组\(c_1\)中,把位置\(r+1\)上的数减\((r+1)*d\)。
//AcWing 243. 一个简单的整数问题2
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
#define ll long long
#define ull unsigned long long
#define lowbit(x) x & -x
#define endl '\n'
typedef pair<int, int> pir;
const int mod = 1e9 + 10;
const int N = 1e5 + 10;
int n, m, l, r, d;
ll a[N], t1[N], t2[N];
void add(int x, int d, ll t[]) {
for(;x <= n; x += lowbit(x)) t[x] += d;
}
ll ask(int x, ll t[]) {
ll sum = 0;
for(; x; x -= lowbit(x)) sum += t[x];
return sum;
}
int main(void){
IOS
cin >> n >> m;
for(int i = 1; i <= n; i ++ ) {
cin >> a[i];
a[i] += a[i - 1];
}
while(m -- ) {
string s; cin >> s;
if(s == "C") {
cin >> l >> r >> d;
add(l, d, t1); add(r + 1, - d, t1);
add(l, l * d, t2); add(r + 1, - (r + 1) * d, t2);
} else {
cin >> l >> r;
ll x1 = a[r] + (r + 1) * ask(r, t1) - ask(r, t2);
ll x2 = a[l - 1] + l * ask(l - 1, t1) - ask(l - 1, t2);
cout << x1 - x2 << endl;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号