算法基础：定义-时间复杂度-列表查找

1.算法定义 

 

算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。

一个算法应该具有以下七个重要的特征：

①有穷性（Finiteness）：算法的有穷性是指算法必须能在执行有限个步骤之后终止；

②确切性(Definiteness)：算法的每一步骤必须有确切的定义；

③输入项(Input)：一个算法有0个或多个输入，以刻画运算对象的初始情况，所谓0个输     入是指算法本身定出了初始条件；

④输出项(Output)：一个算法有一个或多个输出，以反映对输入数据加工后的结果。没       有输出的算法是毫无意义的；

⑤可行性(Effectiveness)：算法中执行的任何计算步骤都是可以被分解为基本的可执行       的操作步，即每个计算步都可以在有限时间内完成（也称之为有效性）；

⑥高效性(High efficiency)：执行速度快，占用资源少；

⑦健壮性(Robustness)：对数据响应正确。

2、复习递归

看下面四个函数，那个是正常的递归

def func1(x):
    print(x)
    func1(x-1)

没有结束，会跑死

def func2(x):
    if x > 0:
        print(x)
        func2(x+1)

递归是越来越小，而这个是越来越大，也会跑死

def func3(x):
    if x > 0:
        print(x)
        func3(x-1)

第三个可以

def func4(x):
    if x > 0:
        func4(x - 1)
        print(x)

第四个也可以

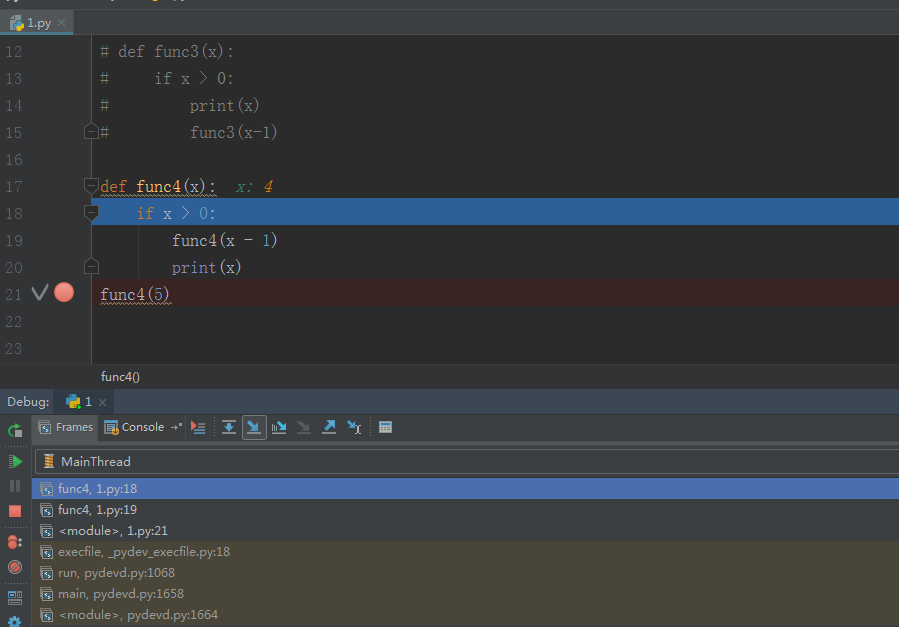
函数3和函数4的区别

def func4(x):
    if x > 0:
        func4(x - 1)
        print(x)
func4(5)

"D:\Program Files\Python35\python3.exe" D:/python13/day32/1.py
1
2
3
4
5

Process finished with exit code 0

def func3(x):
    if x > 0:
        print(x)
        func3(x-1)
func3(5)

"D:\Program Files\Python35\python3.exe" D:/python13/day32/1.py
5
4
3
2
1

Process finished with exit code 0

3. 时间复杂度

计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间,时间复杂度常用大O符号（大O符号（Big O notation）是用于描述函数渐进行为的数学符号。更确切地说，它是用另一个（通常更简单的）函数来描述一个函数数量级的渐近上界。在数学中，它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项；在计算机科学中，它在分析算法复杂性的方面非常有用。）表述，使用这种方式时，时间复杂度可被称为是渐近的，它考察当输入值大小趋近无穷时的情况。

大O，简而言之可以认为它的含义是“order of”（大约是）。

无穷大渐近
大O符号在分析算法效率的时候非常有用。举个例子，解决一个规模为 n 的问题所花费的时间（或者所需步骤的数目）可以被求得：T(n) = 4n^2 - 2n + 2。
当 n 增大时，n^2; 项将开始占主导地位，而其他各项可以被忽略——举例说明：当 n = 500，4n^2; 项是 2n 项的1000倍大，因此在大多数场合下，省略后者对表达式的值的影响将是可以忽略不计的。

计算方法：

1.一个算法执行所耗费的时间：

从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。

一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

2.一般情况下：

算法的基本操作重复执行的次数是模块n的某一个函数f（n），因此，算法的时间复杂度记做：T（n）=O（f（n））。随着模块n的增大，算法执行的时间的增长率和f（n）的增长率成正比，所以f（n）越小，算法的时间复杂度越低，算法的效率越高。

在计算时间复杂度的时候，先找出算法的基本操作，然后根据相应的各语句确定它的执行次数，再找出T（n）的同数量级（它的同数量级有以下：1，Log2n ，n ，nLog2n ，n的平方，n的三次方，2的n次方，n！），找出后，f（n）=该数量级，若T(n)/f(n)求极限可得到一常数c，则时间复杂度T（n）=O（f（n））。

3.常见的时间复杂度

按数量级递增排列，常见的时间复杂度有：

常数阶O(1),  对数阶O(log2n),  线性阶O(n),  线性对数阶O(nlog2n),  平方阶O(n^2)， 立方阶O(n^3),...， k次方阶O(n^k), 指数阶O(2^n) 。

其中，

1.O(n)，O(n^2)， 立方阶O(n^3),...， k次方阶O(n^k) 为多项式阶时间复杂度，分别称为一阶时间复杂度，二阶时间复杂度。。。。

2.O(2^n)，指数阶时间复杂度，该种不实用

3.对数阶O(log2n),   线性对数阶O(nlog2n)，除了常数阶以外，该种效率最高

例：算法：

  for（i=1;i<=n;++i）
  {
     for(j=1;j<=n;++j)
     {
         c[ i ][ j ]=0; //该步骤属于基本操作 执行次数：n^2
          for(k=1;k<=n;++k)
               c[ i ][ j ]+=a[ i ][ k ]*b[ k ][ j ]; //该步骤属于基本操作 执行次数：n^3
     }
  }

  则有 T（n）= n^2+n^3，根据上面括号里的同数量级，我们可以确定 n^3为T（n）的同数量级
  则有f（n）= n^3，然后根据T（n）/f（n）求极限可得到常数c
  则该算法的 时间复杂度：T（n）=O（n^3)

 n和logn那个快？

 

时间复杂度小结：

 空间复杂度

 时间复杂度占用的是时间，空间复杂度占用的是内存

列表查找

概述

二分查找

 

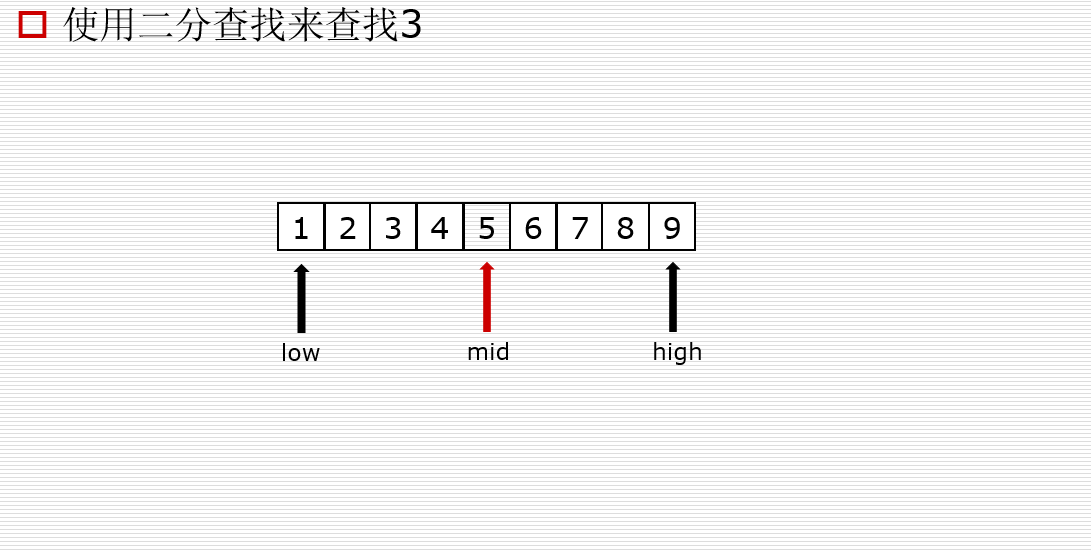
 为什么二分查找快？是因为有序，每次把空间缩小一半

def bin_search(data_set, val):
    low = 0
    high = len(data_set) - 1
    while low <= high:
        mid = (low+high)//2
        if data_set[mid] == val:
            return mid
        elif data_set[mid] < val:
            low = mid + 1
        else:
            high = mid - 1
    return

alex的二分查找

def binary_search(dataset, find_num):
    if len(dataset) > 1:
        mid = int(len(dataset) / 2)
        if dataset[mid] == find_num:
            #print("Find it")
            return dataset[mid]
        elif dataset[mid] > find_num:
            return binary_search(dataset[0:mid], find_num)
        else:
            return binary_search(dataset[mid + 1:], find_num)
    else:
        if dataset[0] == find_num:
            #print("Find it")
            return dataset[0]
        else:
            pass
            #print("Cannot find it.")

两个比较

import time
import random

def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__, t2 - t1))
        return result
    return wrapper

@cal_time
def bin_search(data_set, val):
    low = 0
    high = len(data_set) - 1
    while low <= high:
        mid = (low+high)//2
        if data_set[mid] == val:
            return mid
        elif data_set[mid] < val:
            low = mid + 1
        else:
            high = mid - 1
    return


def binary_search(dataset, find_num):
    if len(dataset) > 1:
        mid = int(len(dataset) / 2)
        if dataset[mid] == find_num:
            #print("Find it")
            return dataset[mid]
        elif dataset[mid] > find_num:
            return binary_search(dataset[0:mid], find_num)
        else:
            return binary_search(dataset[mid + 1:], find_num)
    else:
        if dataset[0] == find_num:
            #print("Find it")
            return dataset[0]
        else:
            pass
            #print("Cannot find it.")

@cal_time
def binary_search_alex(data_set, val):
    return binary_search(data_set, val)


def random_list(n):
    result = []
    ids = list(range(1001,1001+n))
    a1 = ['zhao','qian','sun','li']
    a2 = ['li','hao','','']
    a3 = ['qiang','guo']
    for i in range(n):
        age = random.randint(18,60)
        id = ids[i]
        name = random.choice(a1)+random.choice(a2)+random.choice(a3)

data = list(range(100000000))

print(bin_search(data, 173320))
print(binary_search_alex(data, 173320))

　打印结果如下：

"D:\Program Files\Python35\python3.exe" D:/python13/day32/2.py
bin_search running time: 0.0 secs.
173320
binary_search_alex running time: 2.128999948501587 secs.
173320

Process finished with exit code 0

　慢主要是慢在切片上，因为切片是非常消耗时间的 ，因为要复制一份

列表排序总结：