计算机图形学|二维线段与多边形裁剪算法
裁剪是计算机图形学中的核心问题之一,它决定了哪些图形部分在视窗内可见,哪些需要被剪裁掉。本次实验实现了两种经典的裁剪算法:Cohen-Sutherland线段裁剪算法和Sutherland-Hodgman多边形裁剪算法
一、Cohen-Sutherland线段裁剪算法
算法原理
Cohen-Sutherland算法是计算机图形学中最早、最著名的线段裁剪算法之一。它基于区域编码的概念,通过快速拒绝完全在窗口外部的线段,并逐步裁剪部分在窗口内部的线段。
区域编码系统
算法将二维平面划分为9个区域,每个区域用一个4位二进制码表示:
- 第0位(最低位):点在窗口下方(y < ymin)
- 第1位:点在窗口上方(y > ymax)
- 第2位:点在窗口右侧(x > xmax)
- 第3位:点在窗口左侧(x < xmin)
编码规则:
INSIDE, LEFT, RIGHT, BOTTOM, TOP = 0, 1, 2, 4, 8
def compute_code(x, y, win):
code = INSIDE
xmin, ymin, xmax, ymax = win
if x < xmin:
code |= LEFT # 设置第3位为1
elif x > xmax:
code |= RIGHT # 设置第2位为1
if y < ymin:
code |= BOTTOM # 设置第0位为1
elif y > ymax:
code |= TOP # 设置第1位为1
return code
算法步骤
- 计算端点编码:计算线段两个端点的区域编码
- 完全接受测试:如果两个端点编码都为0(都在窗口内),则接受整个线段
- 完全拒绝测试:如果两个端点编码的逻辑与(AND)不为0,则线段完全在窗口外,拒绝
- 部分裁剪:如果上述测试都不满足,则线段部分在窗口内,需要计算交点进行裁剪
关键实现
def cohen_sutherland_clip(p1, p2, win):
x1, y1 = p1
x2, y2 = p2
xmin, ymin, xmax, ymax = win
code1 = compute_code(x1, y1, win) # 计算端点1的编码
code2 = compute_code(x2, y2, win) # 计算端点2的编码
accept = False
while True:
# 情况1:完全在窗口内(两个编码都为0)
if not (code1 | code2):
accept = True
break
# 情况2:完全在窗口外(两个编码有公共的1位)
elif code1 & code2:
break
# 情况3:部分在窗口内,需要裁剪
else:
# 选择在窗口外的端点(如果code1在窗口外则选code1,否则选code2)
code_out = code1 if code1 else code2
# 计算与窗口边界的交点
if code_out & TOP: # 与上边界相交
x = x1 + (x2 - x1) * (ymax - y1) / (y2 - y1)
y = ymax
elif code_out & BOTTOM: # 与下边界相交
x = x1 + (x2 - x1) * (ymin - y1) / (y2 - y1)
y = ymin
elif code_out & RIGHT: # 与右边界相交
y = y1 + (y2 - y1) * (xmax - x1) / (x2 - x1)
x = xmax
elif code_out & LEFT: # 与左边界相交
y = y1 + (y2 - y1) * (xmin - x1) / (x2 - x1)
x = xmin
# 用交点替换窗口外的端点,并更新编码
if code_out == code1:
x1, y1 = x, y
code1 = compute_code(x1, y1, win)
else:
x2, y2 = x, y
code2 = compute_code(x2, y2, win)
if accept:
return [(int(x1), int(y1)), (int(x2), int(y2))]
else:
return None
算法特点
- 效率高:通过简单的位运算快速判断线段与窗口的关系
- 递归性:通过循环逐步裁剪,直到线段完全在窗口内或完全被拒绝
- 数值稳定性:使用浮点数计算交点,确保精度
二、Sutherland-Hodgman多边形裁剪算法
算法原理
Sutherland-Hodgman算法采用分而治之的策略,将多边形依次用窗口的四个边界(左、右、下、上)进行裁剪。每次裁剪都会产生一个新的多边形顶点序列,作为下一次裁剪的输入。
算法步骤
- 初始化:将原始多边形作为当前多边形
- 边界裁剪:依次用窗口的四条边界(通常按左、右、下、上顺序)裁剪当前多边形
- 顶点处理:对于每条边界,处理多边形的每一条边(由当前顶点和前一个顶点组成)
- 输出生成:每次边界裁剪后生成新的顶点序列
关键实现
def sutherland_hodgman_clip(poly, win):
def clip_edge(poly, edge):
out = []
n = len(poly)
for i in range(n):
curr = poly[i] # 当前顶点
prev = poly[i-1] # 前一个顶点(循环处理)
# 四种情况的处理
# 情况1:当前顶点在边界内,前一个在边界外 -> 添加交点
# 情况2:当前顶点在边界内,前一个也在边界内 -> 添加当前顶点
# 情况3:当前顶点在边界外,前一个在边界内 -> 添加交点
# 情况4:当前顶点在边界外,前一个也在边界外 -> 不添加任何点
if inside(curr, edge, win): # 当前顶点在边界内
if not inside(prev, edge, win): # 前一个顶点在边界外
# 计算边与边界的交点并添加
out.append(intersect(prev, curr, edge, win))
out.append(curr) # 添加当前顶点
elif inside(prev, edge, win): # 当前顶点在边界外,前一个在边界内
# 计算边与边界的交点并添加
out.append(intersect(prev, curr, edge, win))
return out
# 依次用四条边界裁剪多边形
for edge in ['LEFT', 'RIGHT', 'BOTTOM', 'TOP']:
poly = clip_edge(poly, edge)
if not poly: # 如果多边形为空,提前结束
break
return poly
辅助函数:点在边界内的判断
def inside(p, edge, win):
x, y = p
xmin, ymin, xmax, ymax = win
if edge == 'LEFT':
return x >= xmin # 点在左边界右侧
if edge == 'RIGHT':
return x <= xmax # 点在右边界左侧
if edge == 'BOTTOM':
return y >= ymin # 点在下边界上方
if edge == 'TOP':
return y <= ymax # 点在上边界下方
辅助函数:计算边与边界的交点
def intersect(p1, p2, edge, win):
x1, y1 = p1
x2, y2 = p2
xmin, ymin, xmax, ymax = win
if edge == 'LEFT':
x = xmin
y = y1 + (y2 - y1) * (xmin - x1) / (x2 - x1) # 线性插值
elif edge == 'RIGHT':
x = xmax
y = y1 + (y2 - y1) * (xmax - x1) / (x2 - x1)
elif edge == 'BOTTOM':
y = ymin
x = x1 + (x2 - x1) * (ymin - y1) / (y2 - y1)
elif edge == 'TOP':
y = ymax
x = x1 + (x2 - x1) * (ymax - y1) / (y2 - y1)
return (int(x), int(y))
算法特点
- 通用性强:适用于任意凸多边形窗口(本实验实现的是矩形窗口)
- 简单直观:通过依次处理四条边界,逻辑清晰
- 保持拓扑结构:裁剪后仍为多边形,便于后续处理
- 可能产生退化边:在某些情况下可能产生共线的顶点
三、算法比较与选择
Cohen-Sutherland线段裁剪
- 适用场景:线段裁剪,特别是当大量线段需要快速判断时
- 优点:
- 快速拒绝完全不可见的线段
- 算法简单,计算量小
- 适合硬件实现
- 缺点:
- 对于长线段可能需要多次迭代
- 仅适用于线段,不适用于多边形
Sutherland-Hodgman多边形裁剪
- 适用场景:多边形裁剪,特别是当需要保持多边形拓扑结构时
- 优点:
- 可以处理任意凸多边形窗口
- 算法结构清晰,易于实现
- 裁剪结果仍为多边形
- 缺点:
- 对于凹多边形裁剪可能产生多个分离的多边形
- 可能产生退化顶点
四、算法应用与扩展
1. 三维裁剪扩展
两种算法都可以扩展到三维空间:
- Cohen-Sutherland扩展到三维需要6位编码(增加前、后两个方向)
- Sutherland-Hodgman扩展到三维需要6次裁剪(增加近、远两个平面)
2. 其他裁剪算法
- Liang-Barsky算法:参数化线段裁剪,效率更高
- Weiler-Atherton算法:支持凹多边形窗口和凹多边形裁剪
3. 实际应用
- 视口裁剪:在图形渲染管线中,将物体裁剪到视锥体内
- 窗口系统:在GUI中裁剪窗口内容
- 地图显示:在地理信息系统中裁剪地图数据
五、实验结果与分析
通过本实验,我们实现了两种经典的裁剪算法,并验证了它们的正确性:
-
Cohen-Sutherland算法:能够正确裁剪各种位置的线段,包括完全在窗口内、完全在窗口外、部分在窗口内等所有情况。
-
Sutherland-Hodgman算法:能够正确裁剪任意多边形,保持多边形的拓扑结构,正确处理多边形与窗口边界的所有交点。
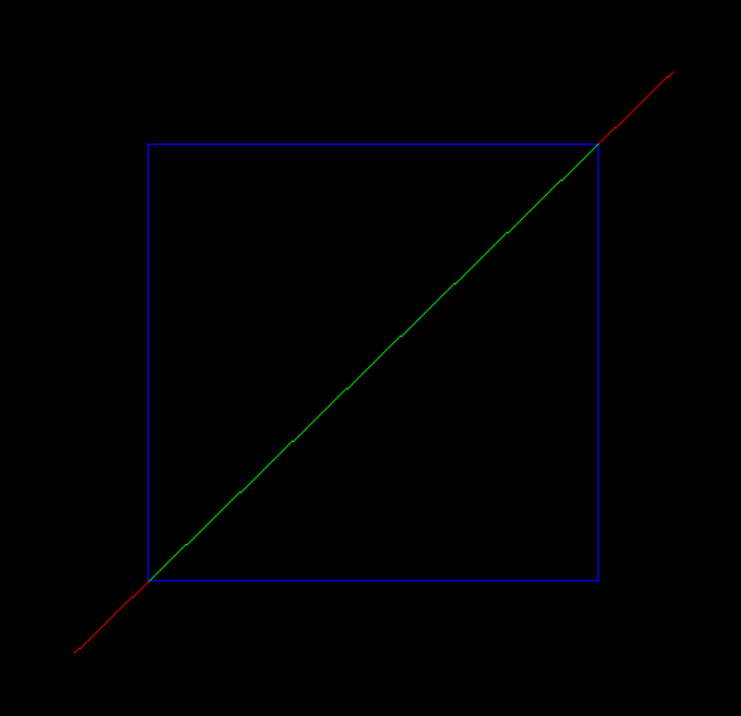
结果
- 蓝色:裁剪窗口边界
- 红色:原始图元(线段或多边形)
- 绿色:裁剪后的结果

性能分析
- 时间复杂度:
- Cohen-Sutherland:最坏情况下O(k),其中k是线段需要裁剪的次数
- Sutherland-Hodgman:O(n×m),其中n是多边形顶点数,m是边界数(通常为4)
- 空间复杂度:
- 两种算法都是O(n),需要存储顶点序列
代码
# 实验三:二维线段与多边形裁剪(PyOpenGL + GLUT)
# Cohen-Sutherland 线段裁剪 & Sutherland-Hodgman 多边形裁剪
from OpenGL.GL import *
from OpenGL.GLUT import *
from OpenGL.GLU import *
# 裁剪窗口 [xmin, ymin, xmax, ymax]
window = [100, 100, 400, 400]
# 线段起点终点
line = [(50, 50), (450, 450)]
# 多边形顶点
polygon = [(120, 120), (380, 120), (420, 300), (250, 420), (120, 380)]
mode = 'line' # 'line' or 'polygon'
INSIDE, LEFT, RIGHT, BOTTOM, TOP = 0, 1, 2, 4, 8
def compute_code(x, y, win):
code = INSIDE
xmin, ymin, xmax, ymax = win
if x < xmin:
code |= LEFT
elif x > xmax:
code |= RIGHT
if y < ymin:
code |= BOTTOM
elif y > ymax:
code |= TOP
return code
def cohen_sutherland_clip(p1, p2, win):
x1, y1 = p1
x2, y2 = p2
xmin, ymin, xmax, ymax = win
code1 = compute_code(x1, y1, win)
code2 = compute_code(x2, y2, win)
accept = False
while True:
if not (code1 | code2):
accept = True
break
elif code1 & code2:
break
else:
code_out = code1 if code1 else code2
if code_out & TOP:
x = x1 + (x2 - x1) * (ymax - y1) / (y2 - y1)
y = ymax
elif code_out & BOTTOM:
x = x1 + (x2 - x1) * (ymin - y1) / (y2 - y1)
y = ymin
elif code_out & RIGHT:
y = y1 + (y2 - y1) * (xmax - x1) / (x2 - x1)
x = xmax
elif code_out & LEFT:
y = y1 + (y2 - y1) * (xmin - x1) / (x2 - x1)
x = xmin
if code_out == code1:
x1, y1 = x, y
code1 = compute_code(x1, y1, win)
else:
x2, y2 = x, y
code2 = compute_code(x2, y2, win)
if accept:
return [(int(x1), int(y1)), (int(x2), int(y2))]
else:
return None
def inside(p, edge, win):
x, y = p
xmin, ymin, xmax, ymax = win
if edge == 'LEFT':
return x >= xmin
if edge == 'RIGHT':
return x <= xmax
if edge == 'BOTTOM':
return y >= ymin
if edge == 'TOP':
return y <= ymax
def intersect(p1, p2, edge, win):
x1, y1 = p1
x2, y2 = p2
xmin, ymin, xmax, ymax = win
if edge == 'LEFT':
x = xmin
y = y1 + (y2 - y1) * (xmin - x1) / (x2 - x1)
elif edge == 'RIGHT':
x = xmax
y = y1 + (y2 - y1) * (xmax - x1) / (x2 - x1)
elif edge == 'BOTTOM':
y = ymin
x = x1 + (x2 - x1) * (ymin - y1) / (y2 - y1)
elif edge == 'TOP':
y = ymax
x = x1 + (x2 - x1) * (ymax - y1) / (y2 - y1)
return (int(x), int(y))
def sutherland_hodgman_clip(poly, win):
def clip_edge(poly, edge):
out = []
n = len(poly)
for i in range(n):
curr, prev = poly[i], poly[i-1]
if inside(curr, edge, win):
if not inside(prev, edge, win):
out.append(intersect(prev, curr, edge, win))
out.append(curr)
elif inside(prev, edge, win):
out.append(intersect(prev, curr, edge, win))
return out
for edge in ['LEFT', 'RIGHT', 'BOTTOM', 'TOP']:
poly = clip_edge(poly, edge)
if not poly:
break
return poly
def prompt_inputs():
"""从控制台读取裁剪窗口与图元(线段或多边形)数据,回车可接受默认值。"""
global window, line, polygon, mode
try:
print('\n--- 裁剪输入配置(回车使用默认值) ---')
print('当前裁剪窗口:', window)
s = input('使用默认裁剪窗口? (y/n) [y]: ').strip().lower()
if s == 'n':
vals = input('输入 xmin ymin xmax ymax(以空格分隔):').strip()
parts = vals.split()
if len(parts) == 4:
window = [int(float(v)) for v in parts]
print('当前模式:', mode)
s = input('选择模式 1=线段, 2=多边形, 回车保持当前: ').strip()
if s == '1':
mode = 'line'
print('当前线段:', line)
s2 = input('使用默认线段? (y/n) [y]: ').strip().lower()
if s2 == 'n':
vals = input('输入 x1 y1 x2 y2(空格分隔):').strip()
p = list(map(float, vals.split()))
if len(p) == 4:
line = [(int(p[0]), int(p[1])), (int(p[2]), int(p[3]))]
elif s == '2':
mode = 'polygon'
print('当前多边形顶点:', polygon)
s2 = input('使用默认多边形? (y/n) [y]: ').strip().lower()
if s2 == 'n':
n = int(input('输入顶点数量: ').strip())
pts = []
for i in range(n):
vals = input(f'第{i+1}个顶点 x y(空格分隔):').strip()
x, y = map(float, vals.split())
pts.append((int(x), int(y)))
polygon = pts
print('输入完成,按窗口查看裁剪结果(在窗口中按 1/2 切换,按 i 重新输入)\n')
except Exception as e:
print('输入错误,保持默认样例。', e)
def draw_window():
glColor3f(0, 0, 1)
glBegin(GL_LINE_LOOP)
glVertex2i(window[0], window[1])
glVertex2i(window[2], window[1])
glVertex2i(window[2], window[3])
glVertex2i(window[0], window[3])
glEnd()
def draw_line():
glColor3f(1, 0, 0)
glBegin(GL_LINES)
glVertex2i(*line[0])
glVertex2i(*line[1])
glEnd()
def draw_polygon():
glColor3f(1, 0, 0)
glBegin(GL_LINE_LOOP)
for v in polygon:
glVertex2i(*v)
glEnd()
def display():
glClear(GL_COLOR_BUFFER_BIT)
draw_window()
if mode == 'line':
draw_line()
clipped = cohen_sutherland_clip(line[0], line[1], window)
if clipped:
glColor3f(0, 1, 0)
glBegin(GL_LINES)
glVertex2i(*clipped[0])
glVertex2i(*clipped[1])
glEnd()
else:
draw_polygon()
clipped = sutherland_hodgman_clip(polygon, window)
if clipped:
glColor3f(0, 1, 0)
glBegin(GL_LINE_LOOP)
for v in clipped:
glVertex2i(*v)
glEnd()
glFlush()
def keyboard(key, x, y):
global mode
if key == b'1':
mode = 'line'
elif key == b'2':
mode = 'polygon'
elif key == b'i':
# 在运行时也允许重新输入数据
prompt_inputs()
glutPostRedisplay()
def main():
# 启动前允许用户通过控制台输入数据
print('运行 2D 裁剪示例:Cohen-Sutherland(线段) & Sutherland-Hodgman(多边形)')
print('按 1 切换到线段裁剪;按 2 切换到多边形裁剪;按 i 在运行时重新输入数据。')
prompt_inputs()
glutInit()
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB)
glutInitWindowSize(500, 500)
glutCreateWindow(b"2D Clipping Cohen-Sutherland & Sutherland-Hodgman")
gluOrtho2D(0, 500, 0, 500)
glutDisplayFunc(display)
glutKeyboardFunc(keyboard)
glutMainLoop()
if __name__ == '__main__':
main()




 浙公网安备 33010602011771号
浙公网安备 33010602011771号