GCM(Galois/Counter Mode) 认证加密算法实现
项目概述
根据NIST SP 800-38D标准实现 AES-GCM
GHASH、IV 处理、计数器生成、认证标签
AES-GCM加密过程
AES-GCM (Galois/Counter Mode) :
- AES-GCM 将 AES 的 CTR 模式用于保密性,用一个不断递增的计数器块经 AES 加密生成流块 E,用 E 与明文异或得到密文
- 认证则由 GHASH 完成,它在 \(GF(2^{128})\) 域上对 AAD附加认证数据 与密文进行多项式乘法累加
使用的哈希子密钥 \(H = AES_K(0^{128})\) - 最终认证标签 \(T\) = \(MSB\)(\(tlen\), \(S\) xor \(AES_K\)(\(J_0\))),其中 S 是 GHASH 的输出,J0 是初始计数器
- IV(初始化向量)长度为 96 位(12 字节)时,\(J_0 = IV || 0x00000001\)
否则对 IV 做填充并用 GHASH 生成 J0
实现要点:
- GHASH 需要在 \(GF(2^{128})\) 上实现乘法
- 对于长度不是 16 字节整数倍的数据,需要对 AAD 和密文在 GHASH 前按规范使用零填充
- 当明文为空(PTlen = 0)时,规范要求仍能正确计算 GHASH 与 Tag;在此实现中会:
- 在 CTR 流中如果明文为空不产生密文块,记录第一个计数器加密结果(E)用于中间值展示
- GHASH 仅对 AAD 与(空)密文和长度块计算
- 解密过程:先按相同方式计算期望的 Tag 并使用常量时间比较(hmac.compare_digest)验证
验证通过才进行 CTR 解密以防止出错泄露信息
实现
外部引入
使用 PyCryptodome 提供的 AES 块加密
使用Python标准库hmac
使用os.urandom生成随机比特流(经查询是密码学安全的随机数生成器)
更改为实验二中实现的伪随机数
结构
- gf_mul() # 伽罗瓦域运算
- ghash() # GHASH哈希函数
- _derive_j0() # 预计数器块生成
- gcm_encrypt() # 认证加密
- gcm_decrypt() # 认证解密
比特流工具
#utils.py
BLOCK_SIZE = 16
def xor_bytes(a: bytes, b: bytes) -> bytes:
return bytes(x ^ y for x, y in zip(a, b))
def pad128(b: bytes) -> bytes:
if len(b) % BLOCK_SIZE == 0:
return b
return b + b'\x00' * (BLOCK_SIZE - (len(b) % BLOCK_SIZE))
def int_from_bytes(b: bytes) -> int:
return int.from_bytes(b, 'big')
def int_to_bytes(i: int) -> bytes:
return i.to_bytes(16, 'big')
def inc32(counter_block: bytes) -> bytes:
#新值 = (旧值 + 1) mod 2^32
c = bytearray(counter_block)
val = int.from_bytes(c[-4:], 'big')
val = (val + 1) & 0xffffffff
c[-4:] = val.to_bytes(4, 'big')
return bytes(c)
伽罗瓦域\(GF(2^{128})\)
位移和条件异或实现
R_POLY = 0xE1000000000000000000000000000000
def gf_mul(x: int, y: int) -> int:
# GF(2^128) multiply (NIST/IEEE 1619)
z = 0
v = x
for i in range(128):
if (y >> (127 - i)) & 1:
z ^= v
if v & 1:
v = (v >> 1) ^ R_POLY
else:
v >>= 1
return z & ((1 << 128) - 1)
CHASH模块
分别处理AAD和密文,最后添加长度编码
使用块级迭代处理,可进行流式计算
from utils import *
from gf128 import *
def ghash(H: bytes, A: bytes, C: bytes) -> bytes:
# H: 16 bytes (AES_K(0^128))
H_int = int_from_bytes(H)
X = 0
A_padded = pad128(A)
for i in range(0, len(A_padded), 16):
block = int_from_bytes(A_padded[i:i+16])
X = gf_mul(X ^ block, H_int)
C_padded = pad128(C)
for i in range(0, len(C_padded), 16):
block = int_from_bytes(C_padded[i:i+16])
X = gf_mul(X ^ block, H_int)
len_block = (len(A) * 8).to_bytes(8, 'big') + (len(C) * 8).to_bytes(8, 'big')
X = gf_mul(X ^ int_from_bytes(len_block), H_int)
return int_to_bytes(X)
计数器
生成预计数器块\(J_0\)
def _derive_j0(H: bytes, iv: bytes) -> bytes:
if len(iv) == 12:
return iv + b'\x00\x00\x00\x01'
else:
# J0 = GHASH(H, IV)
return ghash(H, b'', iv)
加解密
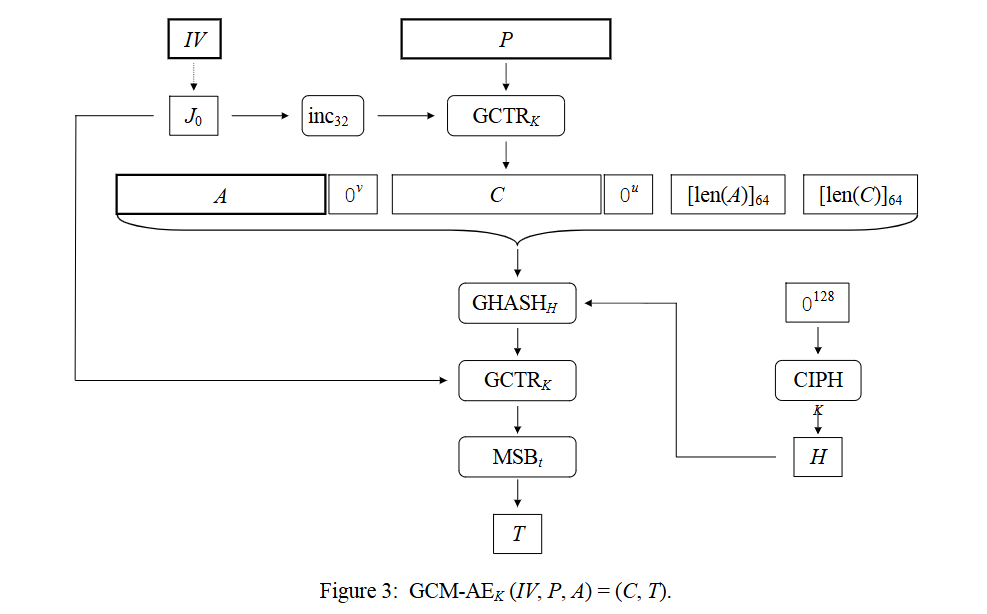
ICB 初始计数器块
CIPH(X) 在密钥 K 下,对数据块 X 应⽤块密码的正向加密函数的输出
GCTR(ICB, X) 对给定的块密码 K 应⽤于⽐特串 X,并使⽤初始计数器块 ICB,GCTR 函数的输出
GHASH(X) 在哈希⼦密钥 H 下,GHASH 函数应⽤于⽐特串 X 的输出
inc(X):新值 = (旧值 + 1) mod 2^32
MSB(X):由 X 的最左边的 s 位组成的位串
加密流程
输入: 密钥(K), 初始化向量(IV), 明文(P), 附加认证数据(AAD)
输出: 密文(C), 认证标签(T)
流程:
- 生成哈希子密钥 \(H = AES_K(0^{128})\)
- 生成预计数器块 \(J_0 = derive_{J_0}(H, IV)\)
- 计数器模式加密 \(C = GCTR_K(inc_{32}(J_0), P)\)
- 计算认证标签 \(T = MSB_t(GCTR_K(J_0, GHASH_H(A||C)))\)
预计数器块\(J_0\)
根据定义
if len(IV) == 96:
IV = [96位IV] || [32位计数器]
J0 = IV || 0x00000001
else:
J0 = GHASH_H(IV || 0^s || [len(IV)]64)
#s = 128 - (len(IV) mod 128)
CTR
明文分块: \(P_1, P_2, P_3, ..., P_n\)
计数器序列: \(CB_1, CB2, CB_3, ..., CB_n\)
密钥流: \(KS_1, KS_2, KS_3, ..., KS_n\)
密文分块: \(C_1, C_2, C_3, ..., C_n\)
其中:
\(CB_1 = inc32(J_0)\)
\(CB_i = inc32(CB_{i-1})\)
\(KS_i = AES_K(CB_i)\)
\(C_i = P_i\) XOR \(K_Si\)
认证标签生成
\(S = GHASH_H(AAD || C || [len(AAD)]_{64} || [len(C)]_{64})\)
\(T = MSB_t(AES_K(J_0), S)\)
解密流程
输入: 密钥(K), 初始化向量(IV), 密文(C), 附加认证数据(AAD), 认证标签(T)
输出: 明文(P) 或 认证失败
流程:
- 重新生成哈希子密钥 \(H = AES_K(0^{128})\)
- 重新生成预计数器块 \(J0 = derive_J0(H, IV)\)
- 重新计算认证标签 \(T' = MSB_t(GCTR_K(J_0, GHASH_H(AAD||C)))\)
- 验证标签: 比较 \(T'\) 与 \(T\)
- 如果验证通过,\(CTR\)解密: \(P = GCTR_K(inc32(J_0), C)\)
功能实现
"""
NIST SP 800-38D AES-GCM
"""
from Crypto.Cipher import AES
import hmac
import os
from utils import xor_bytes, pad128, int_from_bytes, int_to_bytes, inc32
from ghash import ghash
MAX_TAG_LEN = 16
def _derive_j0(H: bytes, iv: bytes) -> bytes:
if len(iv) == 12:
return iv + b'\x00\x00\x00\x01'
else:
# J0 = GHASH(H, IV)
return ghash(H, b'', iv)
def _aes_encrypt_block(key: bytes, block: bytes) -> bytes:
return AES.new(key, AES.MODE_ECB).encrypt(block)
def gcm_encrypt(key: bytes, iv: bytes, plaintext: bytes, aad: bytes = b'', tag_len: int = 16):
if tag_len < 4 or tag_len > MAX_TAG_LEN or tag_len % 2 != 0:
raise ValueError("tag_len must be even and between 4 and 16")
# H = AES_K(0^128)
H = _aes_encrypt_block(key, b'\x00' * 16)
J0 = _derive_j0(H, iv)
counter = inc32(J0)
cipher_stream = b''
cipher = AES.new(key, AES.MODE_ECB)
out = bytearray()
for i in range(0, len(plaintext), 16):
block = plaintext[i:i+16]
s = cipher.encrypt(counter)
counter = inc32(counter)
out_block = xor_bytes(block, s[:len(block)])
out.extend(out_block)
C = bytes(out)
#tag
S = ghash(H, aad, C)
E_J0 = _aes_encrypt_block(key, J0)
tag_full = xor_bytes(E_J0, S)
return C, tag_full[:tag_len]
def gcm_decrypt(key: bytes, iv: bytes, ciphertext: bytes, aad: bytes = b'', tag: bytes = b''):
if len(tag) == 0:
raise ValueError("tag required for decryption")
H = _aes_encrypt_block(key, b'\x00' * 16)
J0 = _derive_j0(H, iv)
counter = inc32(J0)
cipher = AES.new(key, AES.MODE_ECB)
out = bytearray()
for i in range(0, len(ciphertext), 16):
block = ciphertext[i:i+16]
s = cipher.encrypt(counter)
counter = inc32(counter)
out_block = xor_bytes(block, s[:len(block)])
out.extend(out_block)
plaintext = bytes(out)
S = ghash(H, aad, ciphertext)
E_J0 = _aes_encrypt_block(key, J0)
tag_full = xor_bytes(E_J0, S)
expected = tag_full[:len(tag)]
if not hmac.compare_digest(expected, tag):
raise ValueError("authentication failed")
return plaintext
调用验证
if __name__ == "__main__":
key = os.urandom(16)
iv = os.urandom(12)
aad = "1234".encode('utf-8')
pt = "明文".encode('utf-8')
ct, tg = gcm_encrypt(key, iv, pt, aad, tag_len=16)
print("明文:", pt.hex())
print("密文:", ct.hex())
print("tag:", tg.hex())
pt2 = gcm_decrypt(key, iv, ct, aad, tg)
print("验证:", pt2 == pt)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号