密码学|序列密码
序列密码概述
仿照一次一密
将明文编为比特串
产生与明文长度相同的密钥流
加密与解密均为密钥与比特流异或
序列密码的主要任务:设计安全的伪随机密钥产生器
序列密码优缺点
处理速度快,实时性好
适用于军事、外交等保密系统
适应性差,需要密钥同步
线性反馈移位寄存器
一个\(q\)元域 \(GF(q)\)上的 \(n\) 阶反馈移位寄存器:
\(n\) 个寄存器 + 一个反馈函数
最左端寄存器为第1级寄存器,最右端为第n级寄存器
反馈函数
\(f(x_1,\dots ,x_n):GF(q)^n \to GF(q)\)
具有周期状态
LFSR
\(f(x_1,\dots ,x_n) = \sum c_nx_1 + \dots +c_1x_n\)
\([c_1,c_2,\dots ,c_n]\)称为结构常数
第\(i\)阶寄存器的结构常数为\(n+1-i\)
状态转换
将此刻状态计算反馈值
状态左移移位,输出首位,后补反馈值,形成新状态
重复形成周期
输出序列即为一个周期内状态的首位值的序列
\(\tilde{a} = a^{\infty } = a_0a_1a_2\dots a_{n-1}a_n\)
结论:
- n-LFSR的结构由其结构常数唯一确定
- n-LFSR的结构常数与反馈函数互相唯一确定
- n-LFSR序列由其结构常数和初态唯一确定
- 一个n-LFSR可以产生 个不同序列
- 一个n-LFSR的序列的最大周期是
LFSR的有理表示
\(f(x)=1+c_1x+c_2x^2+\dots + c_{n-1}x^{n-1}+c_nx^n\)
\(f(x)\)中常数项\(c_0 = 1\)
称为线性移位寄存器的联接多项式或生成多项式
\(a(x)=a_0+a_1x+a_2x^2\dots +a_{n-1}x^{n-1}+a_nx^n=\sum a_nx^n\)
\(a(x)\)称为序列的形式幂级数或生成函数
\(a(x) = \frac{g(x)}{f(x)}\)
g(x)
n-LFSR有理表示中\(g(x)\)次数小于n
证明略
LFSR : g(x)的系数和结构常数与初态都有关系。
DSR : g(x)的系数就是初态
求\(g(x)\)方法
根据初态,写出a(x)的前n项,次数最高为n-1 ,后
面的项不知道就用+⋯代替。a(x)与f(x)相乘后只取次数小
于等于n-1的项,即为g(x)。 这是因为:g(x)的最高次数为n-1,a(x)的n次以上的
项都会被抵消掉。
m序列
m序列以及其性质
m序列周期为\(2^n-1\),没有全0状态
定理-2:周期为p的序列的(非最简)有理表示为:
\(a(x) = \frac{a_0+a_1x+a_2x^2\dots +a_{p-1}x^{p-1}}{1+x^p}\)
如果\(p = 2^n − 1\),则\(a(x)\)就是n阶寄存器产生的m序列
本原多项式
定理-3:当\(f (x)\)为本原多项式,产生的序列 \(a^~\)为m序列
\(gcd(a_0,a_1,\dots,a_n)=1\)则称\(f(x)\)是唯一分解整环\(D\)上本原多项式
- \(f(x)\)是既约的,即不能再分解因式
- \(f(x)\)可以整除\(x^m+1,m=2^n-1\)
- \(f(x)\)不能整除\(x^q+1,q<m\)
m序列的取样:
设 $\tilde{a} $ 是一个序列 \(\tilde{a}=\{a_0,a_1,a_2,\dots ,a_n,\dots \}\)
\(s\) 是一个正整数,令\(\tilde{a^s}= \{a_0,a_s,a_{2s}\dots \}\)
称 \(\tilde{a^s}\)为序列\(\tilde{a}\) 的s采样
定理-4: 若 \(\tilde{a}\) 是周期为p的m序列,\(s =s_1 mod p\)
则\(\tilde{a^s}=\tilde{a^{s_1}}\)
m序列的伪随机性
三个特性
分布特性
\(s>1,Pr((\xi _1,\xi _2,\dots,\xi _s)=(b_1,b_2,\dots ,b_s)) = 1/2^s\)
相关特性
\(\lim \frac{1}{s}\sum (-1)^{\xi _i}(-1)^{\xi _{i+\tau}}\)
\(= 1,\tau = 0; = 0,\tau >0\)
游程特性
\(𝑃𝑟(𝜉_{i+1} = 𝜉 _{i+2}= ⋯𝜉_{i+k} = 0, 𝜉_{i+k+1} = 1|𝜉_i = 1) = 1/2^{k+1}\)
\(𝑃𝑟(𝜉_{i+1} = 𝜉 _{i+2}= ⋯𝜉_{i+k} = 1, 𝜉_{i+k+1} = 0|𝜉_i = 0) = 1/2^{k+1}\)
m序列具有伪随机性
定理-5: 设\(a^{\infty}\)是n级二元m序列,则
在一个周期中,0和1的出现次数分别为\(2^{n-1}-1,2^{n-1}\)
在一个周期中,游程总数为\(2^{n-1}\)
对于任意的 $ 1\leq i < n-2$
i 长的0游程和1游程都有\(2^{n-i-2}\)个
n-1长的0游程、n长的1游程各有一个;
证明方法:将游程数目转为状态数目
DSR对偶移位寄存器
(DSR: Dual Shift Registers)
LFSR: 也称 Fibonacci LFSRs
DSR: 也称 Galois LFSRs
DSR的状态转换
\(x_1\)是第1级寄存器中的值
新状态 \(= x_1\)(结构常数) ⊕原状态左移一位后补零
若 \(x_1 = 0\),新状态 = 原状态左移一位后补零;
若 \(x_1 = 1\),新状态 =结构常数⊕原状态左移一位后补零。
DSR特殊点
(1) 三个量(寄存器、结构常数和初态)的标记顺序一致;
(2) 反馈只有 \(x_1\)的值;
(3) DSR便于编程实现(反馈不必计算多个量的求和);
(4) DSR的状态不是每一位都输出; (5) DSR与LFSR相同的有理表示产生相同序列;
(6) DSR的有理表示分别对应序列、结构常数和初态。
注意两者结构不同
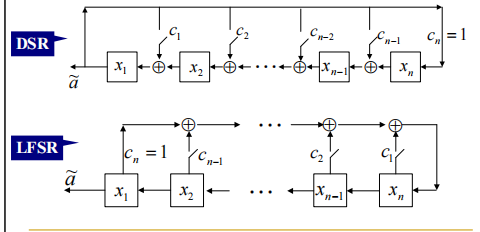
DSR有理表示
\(a(x)=a_0+a_1x+a_2x^2\dots +a_{n-1}x^{n-1}+a_nx^n=\sum a_nx^n\)
\(f(x)=1+c_1x+c_2x^2+\dots + c_{n-1}x^{n-1}+c_nx^n\)
\(g(x)=g_0+g_1x+g_2x^2+\dots + g_{n-1}x^{n-1}\)
\(g(x)\)表示初态
B-M算法
(Berlekamp–Massey)算法
迭代型求解序列生成多项式的算法
B-M 算法不需任何前提,求出产生序列段\(a^N\)的次数最低的联接多项式\(𝑓_N(𝑥)\),即线性综合解
如果知道线性反馈移位寄存器的两个周期,2n长度的序列
就可以通过解方程组求得对应结构常数,得到生成多项式
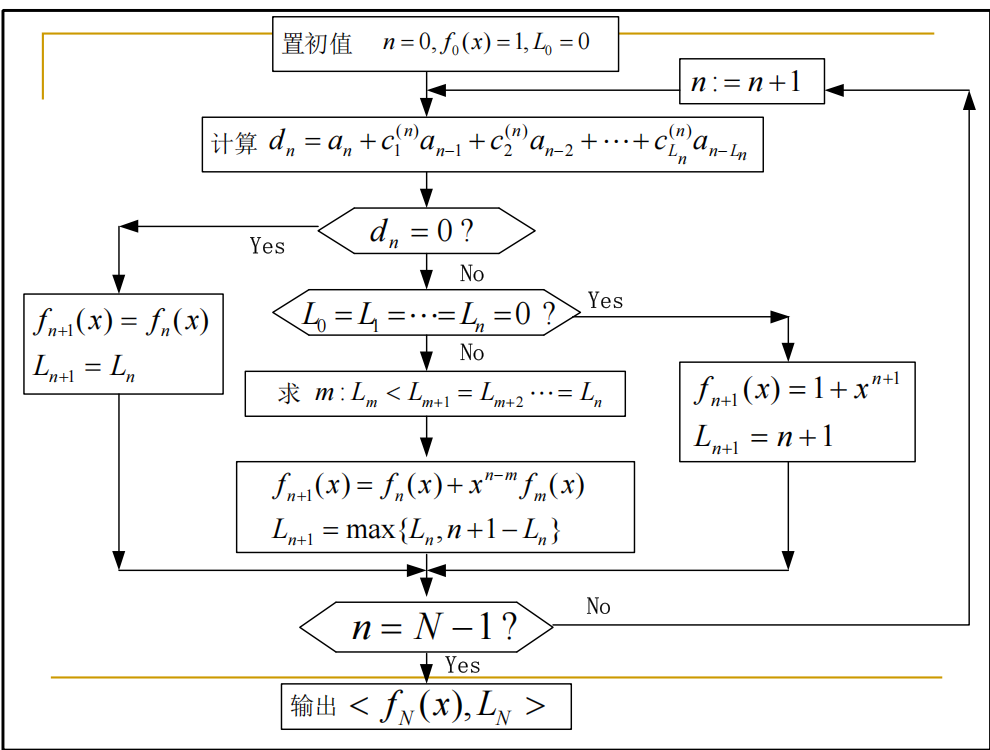
(注意,下面代码由AI生成,不保证正确)
def berlekamp_massey(sequence):
"""
Berlekamp-Massey 算法实现(二元域 GF(2))
输入: sequence - 二进制序列 (0/1 列表)
输出: 生成多项式 f_n (系数列表), L_n (LFSR 长度)
并打印每一步的计算过程
"""
N = len(sequence)
# 初始化变量
n = 0
f = [1] # 初始多项式 f0(x) = 1 (系数列表: [常数项, x^1 系数, x^2 系数, ...])
L = 0 # 当前 LFSR 长度
# 存储历史更新点 (n, f_n, L_n, d_n)
history = []
print("n\ta_n\td_n\tf_n(x)\t\tL_n\tm\tupdate type")
print("-" * 70)
while n < N:
# 计算差异 d_n = a_n + Σ c_i * a_{n-i} (GF(2) 加法即 XOR)
d = sequence[n] # 从 a_n 开始
# 计算反馈项 (c1*a_{n-1} + c2*a_{n-2} + ...)
# 只考虑当前L长度内的系数
for i in range(1, min(L + 1, len(f))):
if n - i >= 0: # 确保不越界
# GF(2) 乘法: AND, 加法: XOR
d ^= f[i] & sequence[n - i]
# 准备输出信息
f_str = "1" # 常数项总是1
# 添加其他项
terms = []
for i in range(1, len(f)):
if f[i] == 1:
terms.append(f"x^{i}" if i > 1 else "x")
if terms:
f_str += " + " + " + ".join(terms)
m_val = ""
update_type = "no update"
if d != 0: # 差异非零,需要更新多项式
if not history: # 首次非零差异(没有历史点)
# 构造新多项式: 1 + x^{n+1}
f_next = [1] + [0] * n + [1]
L_next = n + 1
# 存储当前状态作为历史更新点
history.append((n, f.copy(), L, d))
update_type = "first update"
m_val = ""
else:
# 获取最近的历史点
m, f_m, L_m, d_m = history[-1]
m_val = str(m)
# 计算位移量
shift = n - m
# 构造位移多项式: x^{shift} * f_m(x)
f_shifted = [0] * shift + f_m
# 扩展多项式到相同长度
max_len = max(len(f), len(f_shifted))
f_padded = f + [0] * (max_len - len(f))
fs_padded = f_shifted + [0] * (max_len - len(f_shifted))
# 计算新多项式: f_{n+1}(x) = f_n(x) + x^{n-m} f_m(x)
f_next = [a ^ b for a, b in zip(f_padded, fs_padded)]
# 更新长度: L_{n+1} = max(L_n, n+1 - L_n)
L_next = max(L, n + 1 - L)
# 如果长度增加,保存为新的历史点
if L_next > L:
history.append((n, f.copy(), L, d))
update_type = f"update (m={m})"
else:
# 差异为零,不更新多项式
f_next = f.copy()
L_next = L
update_type = "d=0"
m_val = ""
# 输出当前步骤信息
print(f"{n}\t{sequence[n]}\t{d}\t{f_str:<15}\t{L}\t{m_val}\t{update_type}")
# 更新变量
f = f_next
L = L_next
n += 1
# 输出最终结果
print("\nFinal Result:")
f_str = "1"
terms = []
for i in range(1, len(f)):
if f[i] == 1:
terms.append(f"x^{i}" if i > 1 else "x")
if terms:
f_str += " + " + " + ".join(terms)
print(f"Generating Polynomial: f(x) = {f_str}")
print(f"LFSR Length: L = {L}")
# 返回多项式系数和长度
# 移除尾部多余的零
while len(f) > 1 and f[-1] == 0:
f.pop()
return f, L
已知: LFSR输出序列 \(a_0a_1a_2⋯\),任意一位都是前面若干位的线性反馈值。
开始不知道寄存器的阶数和结构常数, BM算法逐次试验联接多项式,将f(x)从小次数到大次数逐渐增加进行尝试
BM算法更像是一个贪心算法(在对问题求解时,总是做出在当前看来是最好的选择),通过不断增加数来修改线性递推式,每次调整当前递推式时,保证新的递推式满足当前数列的次数最低的递推式。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号