编码理论|总复习

信息的度量

自信息\(I(x_i)\)

某事件不确定性/包含的信息量
\(I(x_i)=-logp(x_i)\)
信息熵\(H(X)\)
表征整个信源的平均不确定性
bit/符号
平均自信息
\(H(X)=-\sum p(x_i)I(x_i)\)

\(X,XY,Y|X\)

互信息\(I(x_i;y_j)\)

从\(y_j\)中获取的\(x_i\)的信息量
\(I(x_i;y_j) = I(x_i) - I(x_i|y_j)\)
\(=-logp(x_i)+logp(x_i|y_j)\)
\(=log \frac{p(x_i|y_j)}{p(x_i)}\)
平均互信息\(I(X;Y)\)
信道中每个码符号实际承载的信息量
信道容量\(C=max{I(X;Y)}\)
\(I(X;Y) = \sum p(x_iy_j)I(x_i;y_j)\)
$ = H(X)-H(X|Y)$

熵

\(p(x|y) = \frac{p(xy)}{p(y)}\)
\(H(XY) = \sum p(xy)logp(xy)\)
\(H(X|Y) = \sum p(x|y)logp(x|y)\)
非负性、确定性、拓展性、连续性、极值性
互信息\(\in R\)
\(I(x_i;y_j)<=I(x_i)\)

熵之间的关系

\(H(XY)=H(X)+H(Y|X)=H(Y)+H(X|Y)\)
\(I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)\)
N维随机变量的（联合）熵
\(𝐻(X)=𝐻(𝑋_1 𝑋_2⋯𝑋_𝑁⋯)\)
无记忆N次扩展信源的熵
\(𝐻(X)=𝐻(𝑋^𝑁)=𝑁𝐻(𝑋)\)

无失真信源编码

信源符号\(\to\) 编码器 \(\to\) 码字
使信源适合于信道的传输
变换后得到的码元接近等概分布，从而提高信息传输的有效性

码的分类

分组码
奇异码
\(\{0,11,00,11\}\)
非奇异码
码字是否相同
非唯一可译码
\(\{0,10,00,01\}\)
唯一可译码
是否正确译码
及时码
\(\{1,01,001,0001\}\)
\(\{00,01,100,101,110\}\)
非及时码
\(\{1,10,100,1000\}\)
收到一个码字后能否立刻译码

平均码长
\(\bar{L}=\sum p(s_i)l_i\)
编码后信息传递率/码率
\(R = \frac{H(S)}{\bar{L}}\)

\(\{s_1:3/4;s_2:1/4\}\)
二次拓展
{ $ a_1=s_1s_1:9/16;a_2=s_1s_2:3/16;a_3=s_2s_1:3/16;a_4=s_2s_2:1/16 $ }
编码：\(\{0,10,110,111\}\)

\(\eta = \frac {𝑅}{log⁡r} =\frac {(𝐻(S))}{(Llog⁡r )}\)
对于二元编码，编码效率\(\eta = \frac{H(S)}{\bar{L}} = R\)

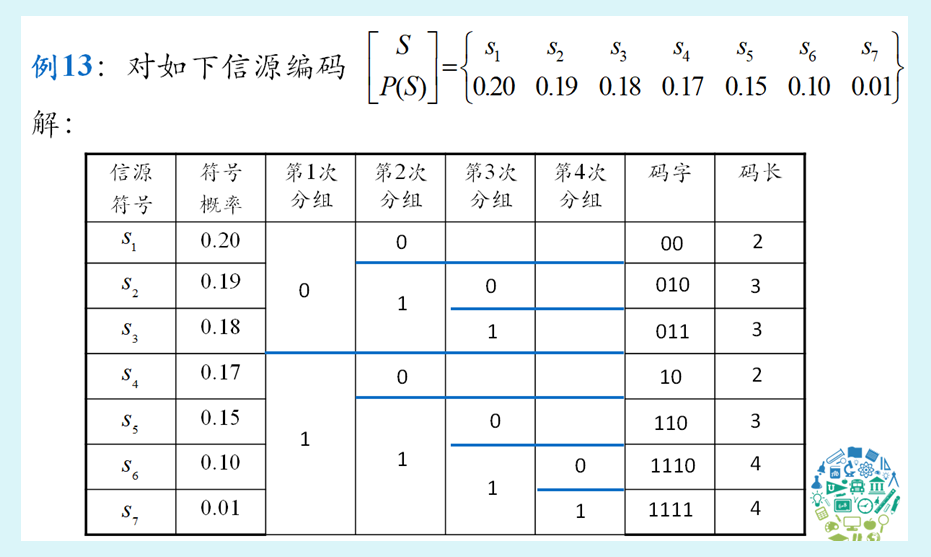
费诺编码

适用于分组概率相等或接近的信源

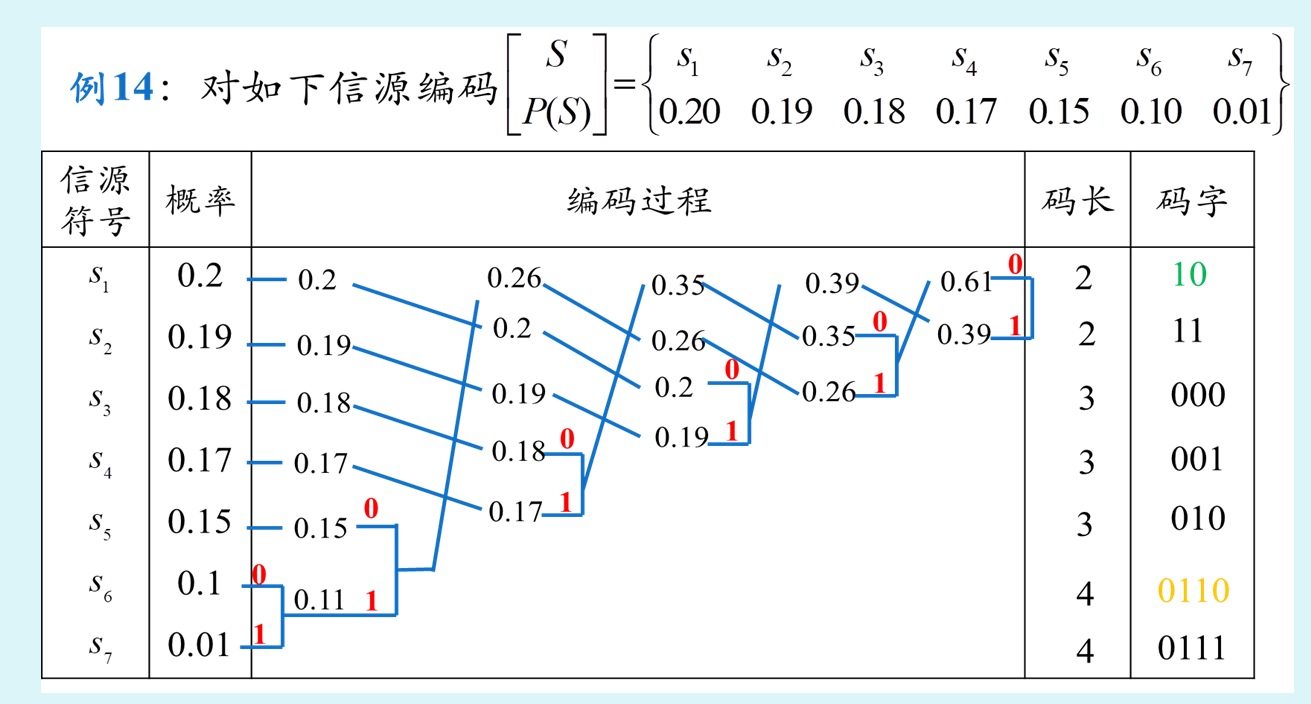
霍夫曼编码

信源缩减排列时，使合并的信源符号位于缩减信源中尽可能高的位置，以充分利用短码

信道及信道容量

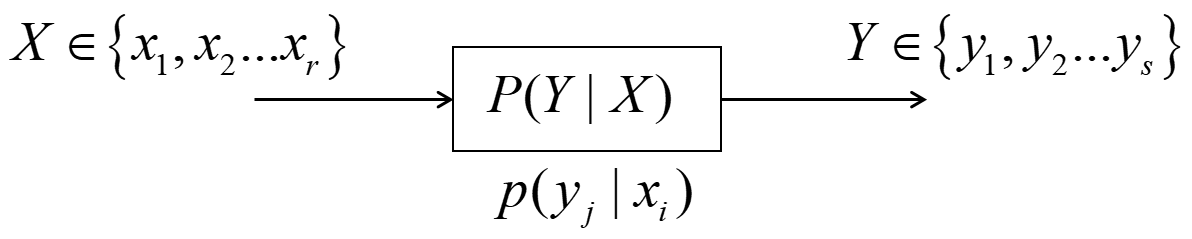
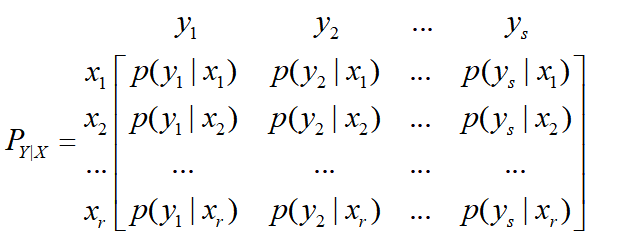
𝑅=𝐼(𝑋;𝑌)=𝐻(𝑋)−𝐻(𝑋|𝑌)
=𝐻(𝑌)−𝐻(𝑌|𝑋)

𝐶=\(max\){𝐼(𝑋;𝑌)} (𝑏𝑖𝑡/𝑠𝑦𝑚)
求信道容量
\(C=logb - \sum^b_{j=1}p(v_j|u_i)log\frac{1}{p(v_j|u_i)}\)

信道传输

\(p(x,u,v,y)\)
信源分布\(p(x)\)
编码与译码\((f,g),f(u|x),g(y|v)\)
信道概率转移矩阵
\(p(v|u)\)
\(p(x,u,v,y)=p(x)f(u|x)p(v|u)g(y|v)\)
即信源发出x，编码为u,传输后为v，译码后为y的概率

损失熵\(H(X|Y)\)
噪声熵\(H(Y|X)\)
无噪信道
\(H(Y|X)=0\)
\(I(X;Y)=H(Y)\to C = max\{I(X;Y)\}=logs\)
无损信道
𝐼(𝑋;𝑌)=𝐻(𝑋)−𝐻(𝑋|𝑌)=𝐻(𝑋)\(C=logr\)

线性分组码

\(H=[Q I]\),\((n-k)\times n\)维
\(P=Q^T,G=[I P]\),\(k\times n\)维
码字序列\(C=mG=\sum m_iG_i\)
\(S=RH^T\)
\(S=0\)时\(R\)是码字
否则传输出错
\(S^T=H_i\)时，第i位出错

循环码

多项式表示
\((n,k)\)循环码
生成多项式\(g(x)\)
校验多项式\(h(x)\)
\(g(x)h(x) = x^n -1\)
生成多项式循环移位\(\to\)生成矩阵
计算 \((x^r M(x))\) 除以 g(x) 的余式 r(x)
\(C(x) = x^r M(x) + r(x)\)

接收\(R = (r_{n-1}, ..., r_0)\)，对应多项式 R(x)。
计算伴随式多项式：计算 \(S(x) = R(x) mod g(x)\)。如果传输没有错误，\(R(x) = C(x) = q(x)g(x)\)，则 S(x) = 0。如果 S(x) ≠ 0，则表示有错误。
单个错误图样 \(E_i(x) = x^i\)其伴随式 \(S_i(x) = E_i(x) mod g(x) = x^i mod g(x)\)
纠正第i位的错误