密码学|分组密码

分组密码概述

扩散与混淆

克服统计分析，采用扩散和混淆两基本方式
扩散：就是使明文的每一位影响密文中的许多位，
这样可以隐蔽明文的统计特性。
混淆：密文的每一位受密钥尽可能多位的影响。
使密文和密钥关系复杂，从而统计分析更加困难。
换位变换(置换/permutation)可以实现有效的扩散。
代替变换(substitution)可以达到比较好的混淆

P置换

def permutation(data, permutation_table):
    """
    执行P置换
    param data: 输入数据，列表或元组
    param permutation_table: 置换表
    return: 置换后的数据
    """
    return [data[i] for i in permutation_table]

def inverse_permutation(permutation_table):
    """
    计算逆P置换表
    param permutation_table: 原始置换表
    return: 逆置换表
    """
    inverse_table = [0] * len(permutation_table)
    for i, pos in enumerate(permutation_table):
        inverse_table[pos] = i
    return inverse_table

分组密码的结构

Feistel结构
每轮处理一半明文，加解密算法相同，代表为DES
SPN结构
每轮处理整个明文分组，加解密算法不同，代表为AES

分组密码的优劣

分组密码：密钥生成简单，同时处理一组明文段，
加密过程复杂，密钥长度固定。
序列密码：产生（伪）随机的密钥流，每次处理一个明文字母。加密过程简单，需要明文与密钥同步。
分组密码适用性更广，易于标准化；
序列密码速度更快，可实时通信

DES

概述

明文分组： 64 bit
密文分组： 64 bit
密钥： 64 bit，其中8bit为校验位，实际 56 bit
轮数： 16 轮
加密函数： 8个 6-4 S盒；P置换。
整体结构： Feistel
关于Feistel结构
参考小规模DES实验
https://www.cnblogs.com/luminescence/p/18904923

具体实现

https://www.cnblogs.com/luminescence/p/18866999

DES的特点

除密钥顺序之外，加密和解密步骤完全相同；
诟病：密钥太短，迭代次数可能太少，
S盒可能存在不安全隐患。

攻击方法

差分分析：一种选择明文攻击，通过分析明文对的差值，对密文对的差值的影响来恢复某些密钥比特。
穷举攻击：人们利用网络并行计算可以在20多小时，破译56位的DES。DES已变得不安全了。
线性分析：一种已知明文攻击，它试图建立起明文、密文和密钥的一组近似线性方程

多重DES

为了提高安全性，防止穷举攻击，DES还有多重形式。

双重DES

\(c = DES_{k_2}(DES_{k_1}(m))\)
\(m = DES^{-1}_{k_1}(DES^{-1}_{k_2}(c))\)
中间相遇攻击
\(c=c = DES_{k_2}(DES_{k_1}(m))\)
\(DES^{-1}_{k_2}(c)=DES_{k_1}(m)\)
总计算量 \(2*2^{56}\)

三重DES

\(c = DES_{k_3}(DES_{k_2}^{-1}(DES_{k_1}(m)))\)
\(m = DES^{-1}_{k_1}(DES_{k_2}(DES^{-1}_{k_3}(c)))\)
中间一层用解密形式是为了可以利用三重DES对单重DES加密的密文进行解密

AES

概述

明文分组： 128 bit
密文分组： 128 bit
密钥： 128、192、256 bit
轮数： 10、12、14 轮（圈）
加密函数： 8-8的S盒、P（行移位、列混合）
密钥生成：扩展、递归
总体结构： SP结构

AES是面向字节的算法：字节为最小单位进行处理。
输入明文分组：128bit=16×8bit＝16个字节，
排成 4×4 的字节数组，称为状态矩阵（State Matrix）
轮函数就是对这个数组进行变换

AES中的运算

AES是面向字节的算法，最小单位是字节(Byte)。
一个字节可用二位十六进制数表示，前加0x表示十六进制

字节运算

一个8比特字节，可以看作\(GF(2^8)\)域中一个元素
AES中用多项式表示
\(b_7b_6b_5b_4b_3b_2b_1b_0\)
\(b_7x^7+b_6x^6+b_5x^5+b_4x^4+b_3x^3+b_2x^2+b_1x+b_0\)
加法就是多项式对应项相加，系数模二加
减法，就是加上减法逆（就是本身）
乘法，要模一个8次既约多项式\(m(x)\)
\(m(x)=x^8+x^4+x^3+x+1\)

每一项多次乘x转化为重复使用xtime( )运算。
复杂运算化简为简单运算的迭代。
\(𝐺𝐹(2^8)\)上的\(xtime( )\)算法：
(1) 如果\(b_7=0\)则xtime( )运算就是左移一位后补零；
(2) 如果\(b_7=1\),则xtime( )左移一位后补零再异或0x1b。

def xtime(byte):
    """
    实现GF(2⁸)上的xtime运算
    """
    if byte & 0x80:
        return ((byte << 1) ^ 0x1B) & 0xFF
    else:
        return (byte << 1) & 0xFF

def gf256_multiply(a, b):
    """
    在GF(2⁸)上计算两个字节的乘法
    xtime分解
    """
    result = 0
    temp = a
    for i in range(8):
        if (b >> i) & 1:
            result ^= temp
        temp = xtime(temp)
    return result

def parse_hex_input(prompt):
    while True:
        s = input(prompt).strip().upper()
        if len(s) == 1 and s in "123456789ABCDEF":
            return int(s, 16)
        elif len(s) == 2 and all(c in "0123456789ABCDEF" for c in s):
            return int(s, 16)
        else:
            print("输入无效")

def stdhex(temp):
    tempstr = str(hex(temp))
    if len(tempstr) == 3:
        tempstr = '0x0' + tempstr[-1]
    return tempstr
if __name__ == '__main__':
    while True:
        a = parse_hex_input("第一个字节: ")
        b = parse_hex_input("第二个字节: ")
        result = gf256_multiply(a, b)
        print(f"结果: {stdhex(a)} * {stdhex(b)} = {stdhex(result)} (十进制: {result})\n")

除法，也就乘以除数的乘法逆。
一般地，可以利用多项式的扩展欧几里得算法求乘法逆。
求a(x)关于不可约多项式m(x)的乘法逆。
根据扩展欧几里得算法，a(x)和m(x)可表示为
\(a(x)b(x) + c(c)m(x) = 1\)
\(a(x)b(x) = 1mod(m(x))\)
\(a(x)^{-1} = b(x)mod(m(x))\)

S盒构造

A=[
    [1 1 1 1 1 0 0 0]
    [0 1 1 1 1 1 0 0]
    [0 0 1 1 1 1 1 0]
    [0 0 0 1 1 1 1 1]
    [1 0 0 0 1 1 1 1]
    [1 1 0 0 0 1 1 1]
    [1 1 1 0 0 0 1 1]
    [1 1 1 1 0 0 0 1]
    ]
C = (1, 1, 0, 0, 0, 1, 1, 0)

s = A * b⁻¹ + c

字节替代例题

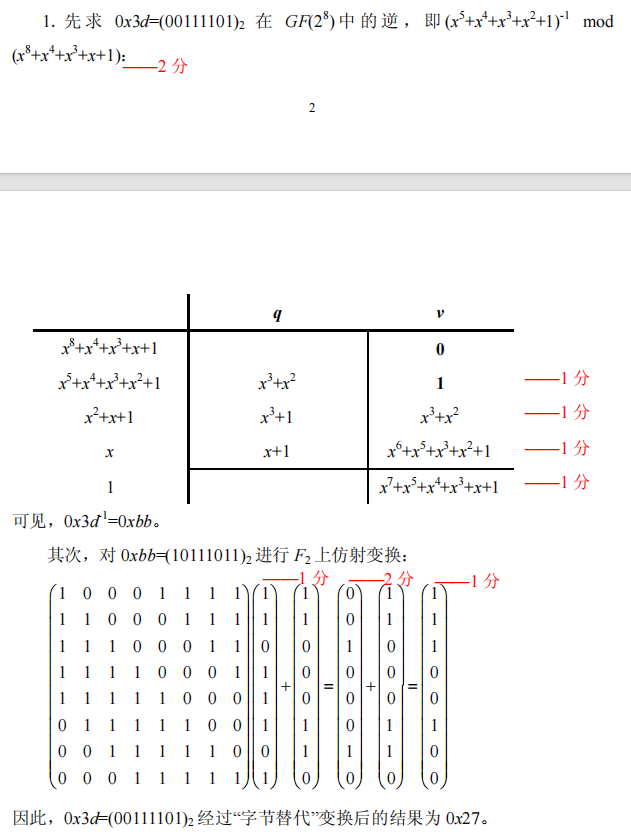
字运算

一个四字节的字可以看作\(GF(2^32)=GF((2^8)^4)\)中的元素
\(a_3a_2a_1a_0\)
用多项式表示
\(a_x^3+a_2x^2+a_1x+a_0\)
加法为对应系数相加，逐位模二加
乘法为多项式相乘后，模一个四次多项式
\(M(x) = \{01\}x^4 + \{01\}\)
\(x^4 + 1=(x^2+1)^2\)

\(d(x)=d_{3} x^{3}+d_{2} x^{2}+d_{1} x+d_0\)
\(=c_{3} x^{3}+\left(c_{2}-c_{6}\right) x^{2}+\left(c_{1}-c_{5}\right) x+\left(c_{0}-c_{4}\right)\)
\(d_0=a_0 \cdot b_0 \oplus a_3 \cdot b_1 \oplus a_2 \cdot b_2 \oplus a_1 \cdot b_3\)
\(d_1=a_1 \cdot b_0 \oplus a_0 \cdot b_1 \oplus a_3 \cdot b_2 \oplus a_2 \cdot b_3\)
\(d_2=a_2 \cdot b_0 \oplus a_1 \cdot b_1 \oplus a_0 \cdot b_2 \oplus a_3 \cdot b_3\)
\(d_3=a_3 \cdot b_0 \oplus a_2 \cdot b_1 \oplus a_1 \cdot b_2 \oplus a_0 \cdot b_3\)
\(\begin{bmatrix} d_0 \\ d_1 \\ d_2 \\ d_3 \end{bmatrix}=\begin{bmatrix} a_0 & a_3 & a_2 & a_1 \\ a_1 & a_0 & a_3 & a_2 \\ a_2 & a_1 & a_0 & a_3 \\ a_3 & a_2 & a_1 & a_0 \end{bmatrix}\begin{bmatrix} b_0 \\ b_1 \\ b_2 \\ b_3 \end{bmatrix}\)

AES的列混合

\(\begin{bmatrix} d_0 \\ d_1 \\ d_2 \\ d_3 \end{bmatrix}=\begin{bmatrix} 02 & 03 & 01 & 01 \\ 01 & 02 & 03 & 01 \\ 01 & 01 & 02 & 03 \\ 03 & 01 & 01 & 02 \end{bmatrix}\begin{bmatrix} b_0 \\ b_1 \\ b_2 \\ b_3 \end{bmatrix}\)
列混合前后，两个矩阵各列上所有元素和是对应相等的

AES的特点

结构简单，适应性强
加解密算法不同，解密使用加密的逆模块

分组密码的工作模式

ECB

电码本模式 electronic codebook
直接分组，相同明文产生相同密文

CBC

密码分组链接模式 Cipher-Block Chaining
使用初始向量与分组1异或，加密后密文1与分组2异或，以此类推
缺点：存在错误扩散
若在信道上传送的第i组密文ci出现1bit错误，则在解密时，将引起第i组明文mi全错及第i+1组明文mi+1出现1bit错误；此外，第j(j>i+1)组明文\(m_j\)将不再受此错误影响，系统会自动恢复正常

CFB

密码反馈模式 Cipher FeedBack
使用移位寄存器产生序列，经过分组密码加密后序列与明文分组异或，使用密文分组生成新序列
可以不按固定位数加密
假设明文分组为j位，首先用初始向量进行操作在移位寄存器得到64位，加密后序列1与明文1异或，得到密文1，丢弃后面\(64-j\)位并填入移位寄存器生成序列2，以此类推
该模式的特点：
存在有限的(其实是\([64/j]+1\)组)错误扩散：当传输的密文组\(c_i\)出现1bit错误时，解密的明文组\(m_i\)也有1bit错误，而且随后解密出来的\([64/j]\)组明文\(m_{i+1},m_{i+2},……,m_{i+[64/j]}\)全错，直至此后原\(c_i\)的1bit错误刚好移出64级移位寄存器，系统可自动恢复正常。
CFB模式给出的是典型的自同步序列密码：只要接收方连续收到\([64/j]\)组正确的密文，收发双方的64级移位寄存器存储的数据就完全一样，从而双方可重新建立起同步。

OFB

输出反馈模式 Output FeedBack
与CFB类似，但下一个移位寄存器直接使用上一个序列的前j位生成新序列
明文分组直接和序列异或后输出密文分组

计数器模式

使用时间戳做生成序列，经过加密后与明文分组异或得到密文分组

posted @ 2025-06-17 15:54 lumiere_cloud 阅读(86) 评论(0) 收藏举报

刷新页面返回顶部

luminescence