信息论|信道及其容量

信息速率

信源在单位时间内输出的熵（平均信息量）称为信源的熵速率,单位：bit/s, nat/s, hat/s
离散信源的熵速率：\(H(X) = -\sum plogp\)
连续信源的熵速率：\(H(X) = -\int p(x)logp(x)dx\)

信道问题：在有噪信道中传输信息，收到的熵与发出的熵差多少

信道的数学模型及分类

通信系统中传递和存储信息的通道或媒介，包括空间传输和时间传输
输入盒输出的关系：转移概率\(p(y|x)\)
信道的描述：

• 输入集合
• 输出集合
• 转移概率分布
  研究目标：从信道的输出了解信道的输入

按信道的输入符号分类

空间 = 状态集合(x,y) + 时间集合T
离散信道（数字信道）：输入输出空间为离散
连续信道：状态集合连续，时间集合离散
模拟信道（波形信道）：输入输出空间为连续

按信道转移概率分布函数的特点分类

有记忆信道：输出 Y不仅与当前的输入 X 有关，而
与前面的输入有关
无记忆信道：输出 Y 仅与当前的输入 X 有关，
而与前面的输入无关

按输入和输出的数目分类

单用户信道：输入和输出都只有一个的单向通信
信道。
多用户信道：输入和输出中至少有一端有两个以
上的用户，且可以进行双向通信。

按信道的统计特性与时间的关系分类

固定参数（恒参）信道：信道的统计特性不
随时间变化。
时变参数（随参）信道：信道的统计特性随
时间变化。

离散、无记忆、恒参
X为发射端，Y为接收端
\(P(x_i \to y_j) = p(\frac{y_j}{x_i}) = p_{ij}\)
发 i 收 j 的概率
无干扰： \(p_{ji} = 1 if j==1 else 0\)

对称二元信道（BSC）

差错概率为p
\(p_{10}=p_(01)=p\)
\(p_{11}=p_(00)=1-p\)

删除信道

\(p_{10}=p_(01)=0\)
\(p_{e1}=p_(e0)\)

Z信道

\(p_{10}=p\)
例如磁盘掉磁

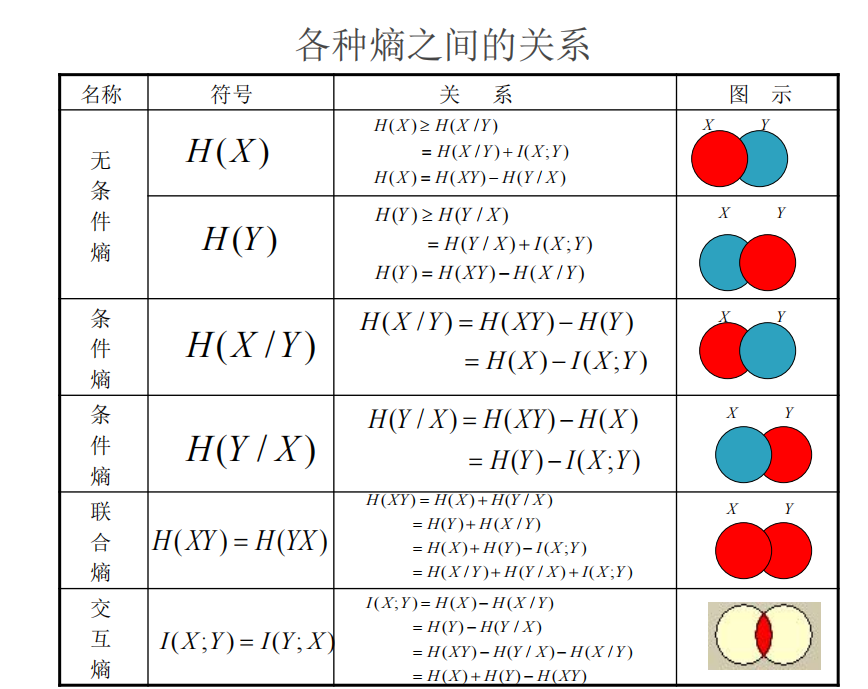
互信息

\(log \frac{1}{p(\frac{x_i}{y_j})}\)为疑义度
收到\(y_j\)后对\(x_i\)的不确定度
平均疑义度：\(H(\frac{X}{Y})\) \(= \sum p(y_j)\)\(\sum p(\frac{x_i}{y_j})\)\(log \frac{1}{p(\frac{x_i}{y_j})}\)
= \(-\sum\sum p(xy)log(\frac{x}{y})\)
收到信号后，对信源仍有不确定度
定义y关于x的互信息：
\(I = H(X ) − H(XY) = I(XY)\)
$H (\frac{Y}{X}) $—散布度（收信端的发散程度）

信道容量

信道提供给收信者的最大信息
\(C=maxI=max[H(X) - H(\frac{X}{Y})]\)
求信道容量问题是约束极值问题及求最大互信息
C 客观反映信道的传输能力，只与信
道特性有关，而与信源无关，表示信
道可能传输的最大信息量。
可以通过编码改变信源的分布使互信息达到最大值
定理：对于信道矩阵为 $ P $ 的离散无记忆信道，其输入分布 $ p(x) $ 能使互信息 $ I(X; Y) $ 达到最大值（信道容量）的充要条件是
$ I(x = a_i; Y) = C, \quad$ 当\(p_i > 0\)
$ I(x = a_i; Y) < C, \quad$ 当$ p_i = 0 $
其中 $ I(x = a_i; Y) = \sum_{j=1}^{m} p(b_j | a_i) \log \frac{p(b_j | a_i)}{\sum_{i=1}^{n} p(a_i) p(b_j | a_i)} $
为 $ a_i 与 Y $ 的互信息，$ C $ 为信道容量。

特殊DMC的信道容量

无噪无损信道

信道转移矩阵为单位矩阵
\(C=maxI=maxH(X)=logn\)

有噪无损信道

信道转移矩阵的每一列有且仅有一个非零元素
\(H(Y|X) \neq 0\)
\(H(X|Y) = 0\)
\(C=maxI=maxH(X)=logn\)

无噪有损信道

信道转移矩阵的每一行有且仅有一个非零元素1
\(H(X|Y) \neq 0\)
\(H(Y|X) = 0\)
\(C=maxI=maxH(Y)=logm\)

对称信道

信道转移矩阵P中所有的行都是同一组元素的不同排列，所有的列也是同一组元素的不同排列
准对称信道：设 B 为信道转移矩阵P的列集合，如果将B划分成m个子集，而用每一个子集构成的矩阵所对应的信道都是对称信道。
定理：对于准对称信道，达到信道容量的输入分布为等概分布。

当信道转移概率矩阵P是非奇异时（此时n = m），即逆矩阵\(P^{-1}\)存在时，该信道被称为可逆矩阵信道。
达到信道容量时输入、输出概率分布的唯一性
一般信道容量的计算方法 :拉格朗日乘子法

独立并行信道的容量为各分信道容量之和

和信道：随机选取信道1或信道2传送，（并信道）。
P (channel) P (channe2) = 1
定理：和信道的容量满足下式
\(2^C = 2^{c_1}+2^{c_2}\)
级联信道：信道1的输出作为信道2的输入。
\(c \neq min\{c_1,c_2\}\)

特殊DMC的信道容量

1. 二进制对称信道（BSC）

• 定义：输入和输出均为二进制符号（0和1），且发生错误的概率为 \(\epsilon\)，正确传输的概率为 \(1 - \epsilon\)
• 转移矩阵：
  \( P = \begin{bmatrix} 1 - \epsilon & \epsilon \\ \epsilon & 1 - \epsilon \end{bmatrix} \)
• 信道容量：
  \( C = 1 - H(\epsilon) \)
  其中 \(H(\epsilon) = -\epsilon \log \epsilon - (1 - \epsilon) \log (1 - \epsilon)\)是二元熵函数。
• 特点：对称性使得最优输入分布为均匀分布（\(q_0 = q_1 = 0.5\)），直接简化了互信息的最大化过程。

---

2. 二进制删除信道（BEC）

• 定义：输入为二进制符号（0和1），输出可能为符号（0、1或删除符号 \(e\)）。
• 转移矩阵：
  \( P = \begin{bmatrix} 1 - \epsilon & 0 & \epsilon \\ 0 & 1 - \epsilon & \epsilon \end{bmatrix} \)
• 信道容量：
  \( C = 1 - H(\epsilon) \)
  其中 \(H(\epsilon)\) 是二元熵函数。
• 特点：删除符号 \(e\) 的出现使得信道容量与BSC相同，但输出符号数增加。

---

3. Z信道

• 定义：输入为二进制符号（0和1），输出为二进制符号（0和1），但错误仅从1到0单向发生。
• 转移矩阵：
  \( P = \begin{bmatrix} 1 & 0 \\ \epsilon & 1 - \epsilon \end{bmatrix} \)
• 信道容量：
  需通过优化输入分布 \(q_0\) 和 \(q_1\) 计算互信息 \(I(X;Y)\)，通常无法解析表达。
• 特点：非对称性导致最优输入分布不为均匀分布，需数值方法求解。

---

4. 对称信道（一般情况）

• 定义：输入和输出符号的转移概率满足对称性条件。
• 信道容量：
  \( C = \log_2 |\mathcal{Y}| - H(Y|X) \)
  其中\(|\mathcal{Y}|\) 是输出符号集的大小，\(H(Y|X)\) 是条件熵。
• 特点：对称性使得最优输入分布为均匀分布，简化计算。

---

5. 输入对称但输出不对称的信道

• 定义：输入符号的转移概率相同，但输出符号的分布不对称。
• 信道容量：
  需通过优化输入分布计算互信息 \(I(X;Y)\)，可能需要迭代方法（如Blahut-Arimoto算法）。
• 特点：计算复杂度较高，但可利用对称性部分简化。

---

计算方法总结

1. 对称信道：直接使用均匀输入分布，计算互信息。
2. 非对称信道：需通过优化输入分布或迭代算法求解。
3. 数值方法：对于复杂信道，可使用Blahut-Arimoto算法迭代计算信道容量。

示例：BSC的容量计算

• 输入分布：均匀分布 \(q_0 = q_1 = 0.5\)
• 输出分布：\(p_0 = p_1 = 0.5\)
• 互信息：
  \( I(X;Y) = H(Y) - H(Y|X) \)
  其中 $ H(Y) = H(0.5) = 1 )，( H(Y|X) = H(\epsilon) $
• 信道容量：
  \( C = 1 - H(\epsilon) \)