信息论|熵
信息量
获得信息量 = 不确定程度平均减少的量
例:八个串联灯泡其中一个故障
测量前信息量\(H(X) = log8 = 3\)
- 二分法测量
第一次测量后确定四个
\(H_2 = log4 = 2\)
获得的信息量为 \(1bit\)
第二次第三次测量同理,获得\(3bit\)信息量后不确定程度减少为\(0\) - 每次测两个
先量1、2,出现两种情况:
1)1、2不通的情况:
1,2 的熵为\(1bit\) 信息量\(2bit\)
2)1、2通的情况:
其余6个熵为\(log6 = 2.58\)
信息量\(0.42bit\)
获得的平均信息量:\(0.811bit\)
测量后概率空间发生变化,表示了信息量的获得
离散信源的熵
事件符合二项分布时
\(\begin{bmatrix} X \\ P(x) \end{bmatrix}\)=\(\begin{bmatrix}
x_1, & x_2 \\
p, & 1-p
\end{bmatrix}\)
p = 0.5 时,\(H_{max} = 1\)
p = 0 or p = 1 时,必然事件 \(H = 0\)
英文信源 二十六个字母加空格
等概率输出时 \(H = log27 = 4.76\)
考虑英文字母的频率 \(H = 4.065\)
熵的性质
-
对称性
\(H(p_1,p_2) = H(P_2,P_1)\) -
非负性
\(H(x) >= 0\) -
确定性
\(H(1) = 0\) -
扩展性

-
强可加性
联合熵\(H(xy)\) = 无条件熵\(H(x)\) + 条件熵\(H(y/x)\) -
递增性
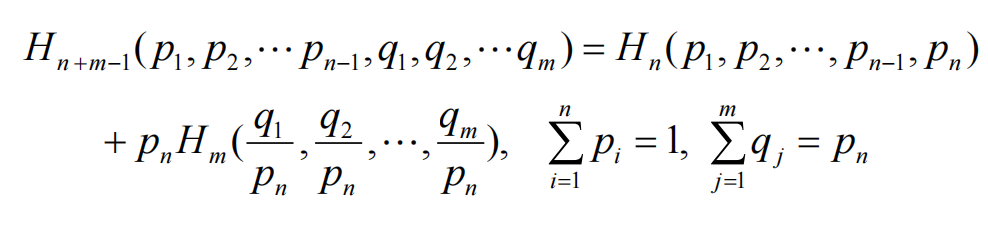
-
极值性
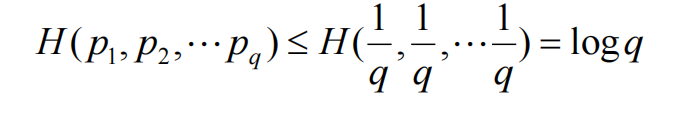
-
上凸性

联合熵
\(H(XY) = - \sum^n_1 \sum^m_1 p(x_iy_j)log p(x_iy_j)\)
性质 \(H(XY) <= H(X) + H(Y)\)
(算术平均 不小于 几何平均)
根据贝叶斯公式
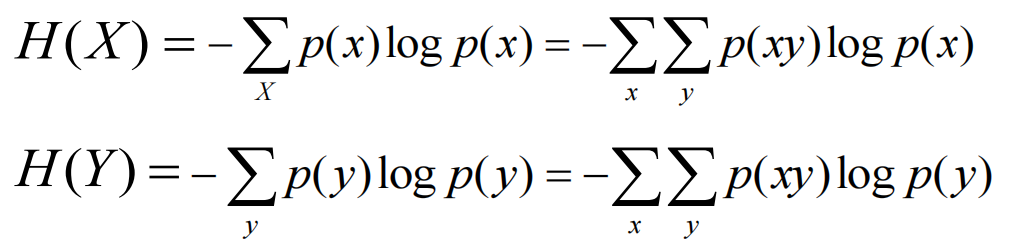
对于独立信源 \(H(XY) = H(X) + H(Y)\)
对于同一信源,称为\(K\)次延长
\(H(X^K) <= KH(X)\)
条件熵
\(H(Y/X)\)
\(H(XY) = H(X) + H(Y/X)= H(Y) + H(X/Y)\)
剩余度
\(\eta = \frac{H(x)}{H_{max}(X)}\)
实际熵/最大熵
多余度 \(E= 1- \eta\)
交互熵
\(I(X;Y) = I(Y;X) = H(X) - H(Y/X)\)
连续信源的熵
信源输出时间和取值连续
可以用随机过程\({x(t)}\)表示
数字化的过程
抽样、量化、编码
根据奈奎斯特取样定理,以 \(f>2w\) 速率取样,样值能代表原信号
信号带宽为 w 信号持续时间长度为:T 样值点为:n=2wT
第i个区间的概率为
\(p_i = \int^{a + i\Delta} _{a + (i-1)\Delta} p(x)dx\)
\(H(X) = -\sum plogp\)
此后连续信源被量化为离散信源
取极限值得到连续信源的信息熵
计算时 \(log\Delta\) 是趋于无穷大的常数,避开此项
定义连续信源的熵:\(H(X) = -\int_R p(x) log p(x)dx\)
只要两者离散逼近时,所取的间隔一致,无限大项常数将互相抵消掉,不影响熵的差值
连续信源的熵是一个比无穷大大多少的相对量,离散信源的熵是绝对量
连续信源的熵的极值
对输出幅度(瞬时功率)受限的信源,其输出最大熵条件是输出在该范围内均匀分布,其输出最大熵为\(p(x)\)的倒数的对数。
平均功率受限条件下,具有正态分布的连续信源,熵最大,其大小随平均功率的增加而增加。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号