ANC滤波器设计相关算法
自适应滤波一般形式有:
- Transversal—finite impulse response (FIR)横向有限脉冲响应
- Recursive—infinite impulse response (IIR)递归无限脉冲响应
- Lattice filters点阵滤波器
- Transform-domain filters转换域滤波器
应用于自适应滤波器的最常用算法是使用最小均方(LMS)算法的横向滤波器。残余噪声可作为自适应算法的误差信号输入用以调整滤波器。
下文中涉及到的一些路径:
- 主要路径$P(z)$:输入麦克风Input microphone(耳机外部麦克风)到误差麦克风error microphone(耳机来说可以看做耳膜)的声学路径
- 次级路径$H(z)$:从扬声器speaker到误差麦克风error microphone的声学路径
- 反馈路径$F(z)$:从从扬声器speaker到输入麦克风input microphone的声学路径
- 次级路径的估计$C(z)$:离线计算好的
- 反馈路径的估计$D(z)$:离线计算好的
- 自适应滤波器$W(z)$:在线更新
一、宽带前馈ANC系统Broadband Feedforward ANC Systems
1、理想情况
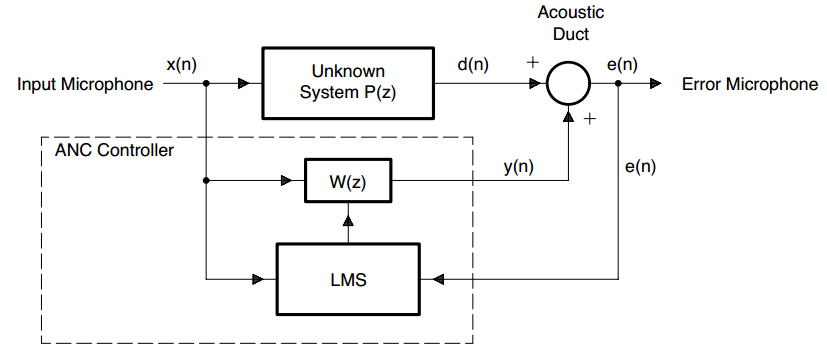
图1,理想情况 宽带前馈ANC系统
理想的有源噪声控制系统使用自适应滤波器$W(z)$来估计参考输入传感器和误差传感器之间未知主声路径$P(z)$的响应。不考虑其他因素影响,误差信号可以表示为:
$E(z)=D(z)+Y(z)=X(z)[P(z)+W(z)]$
如果滤波器收敛,$E(z)=0$,得到
$W(z)=-P(z)$
也即自适应滤波器输出y(n)与主噪声d(n)具有相同幅度并相差180°:
$y(n)=-d(n)$
2、考虑次级路径:Secondary-Path Effects
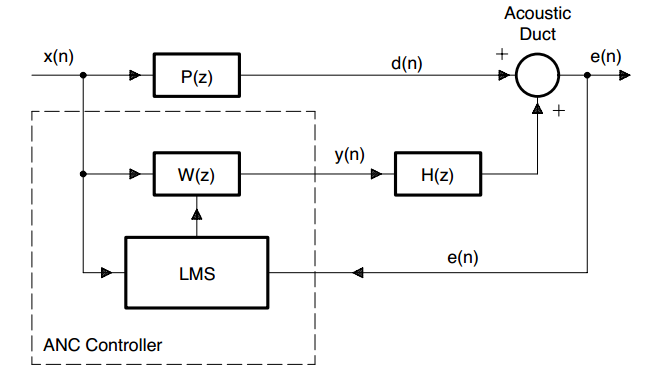
图2,包含次级路径$H(z)$的 宽带前馈ANC系统
次级路径$H(z)$指的是从扬声器Speaker到误差麦克风的声学路径,考虑次级路径得到
$E(z)=X(z)P(z)+X(z)W(z)H(z)$
假设$W(z)$有足够的阶数,如果滤波器收敛,$E(z)=0$,得到
$W(z)=-P(z)/H(z)$
当频率$\omega$存在$H(\omega)=0$时,控制系统是不稳定的。此外,如果有频率$\omega$,其中$P(\omega)=0$,(即主路径上的零导致不可观测的控制频率),控制系统是无效的。因此,次级路径$H(z)$的特性对ANC系统的性能有重要影响。
3、Filtered-X Least-Mean-Square(FXLMS) Algorithm
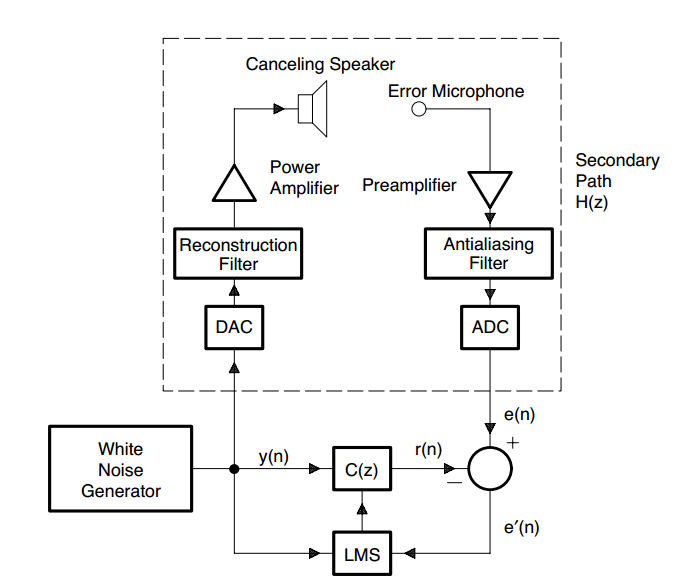
图3,离线估计次级路径$H(z)$,得到$C(z)$
离线估计次级路径$H(z)$,计算步骤如下:
- 播放白噪声\(y(n)\),白噪声作为Canceling Speaker的输出播放,也作为LMS算法的输入;
- Error Microphone采集信号\(e(n)\);
- 计算得到滤波器输出\(r(n)=\sum_{0}^{M-1}c_i(n)y(n-i)\),其中\(c_i(n)\)是自适应滤波器的系数,\(M\)是其阶数;
- 计算误差\({e}' (n)=e(n)-r(n)\);
- 基于LMS算法更新自适应滤波器系数:\(c_i(n+1)=c_i(n)+\mu e{'}(n)y(n-i),i=0,1,...,M-1\);其中\(0<\mu<\frac{1}{MP_y}\),\(\mu\)是算法步长,\(P_y\)是生成的白噪声\(y(n)\)的功率;
- 重复这个过程大约10秒钟。保存自适应滤波器\(C(z)\)的系数(\(C(z)\)是对次级路径\(H(z)\)的估计),并将其用于后续噪声消除模式。
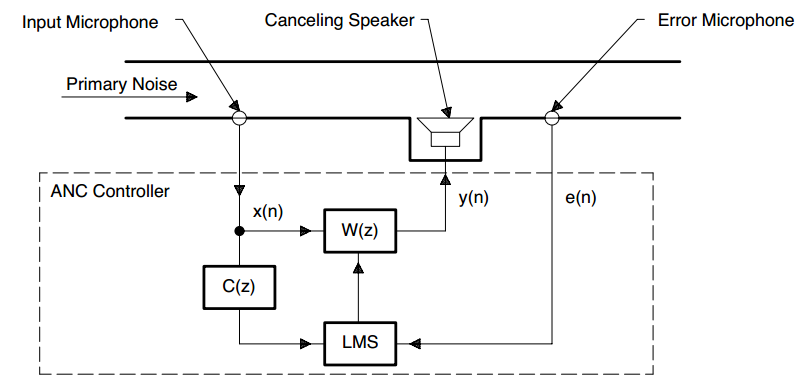
图4,FXLMS算法流程框图-在线更新滤波器
在线估计主要路径,得到$W(z)$,计算流程如下:
- 从输入端口输入参考信号\(x(n)\)(来自输入麦克风)和错误信号\(e(n)\)(来自错误麦克风);
- 计算滤波器输出\(y(n)=\sum_{0}^{M-1}w_i(n)x(n-i)\),其中\(w_i(n)\)是自适应滤波器\(W(z)\)的系数,\(N\)是其阶数;
- 输出antinoise \(y(n)\),驱动扬声器(canceling loudspeaker);
- 得到\({x}’(n)=\sum_{0}^{M-1}c_i(n)x(n-i)\);
- 更新自适应滤波器\(W(z)\):\(w_i(n+1)=w_i(n)+\mu e{'}(n)x(n-i),i=0,1,...,N-1\);
- 为下一次迭代重复此过程。注意,这个算法需要的内存位置总数是2(N + M)加上一些参数。
4、Leaky FXLMS Algorithm
当在固定长度的信号处理器上实现自适应滤波器时,舍入噪声反馈给滤波器权值并不断累积。这可能导致系数增长大于处理器的动态范围(溢出),从而导致不准确的滤波器性能。该问题的一个解决方案是基于添加一个小的强制函数,它倾向于将每个过滤器权重偏向于零。leaky FXLMS 算法如下:
$w(n+1)=vw(n)-\mu e(n)x{’}(n)$
其中泄露因子\(v\)小于1。leaky FXLMS算法不仅可以减小有限精度实现中的数值误差,而且可以限制扬声器的输出功率,避免因对消扬声器过驱动而引起的非线性失真
5、Acoustic Feedback Effects and Solution(FBFXLMS) Algorithm
这里的Acoustic Feedback Effects指的是扬声器的输出(antinoise $y(n)$)到input microphone的反馈。这种声学反馈在模型的响应中引入了一个反馈环或极点,导致控制系统不稳定。一般的的解决方案如下(本文中主要研究2、4点):
- 使用定向麦克风和扬声器;(这有一个限制,定向阵列通常高度依赖于阵列元素的间距,并且只在相对狭窄的频率范围内定向)
- 使用固定的补偿信号(由补偿滤波器产生,其系数由训练信号离线确定)来抵消声学反馈的影响;
- 使用第二个离线自适应滤波器与反馈路径并行;
- 使用自适应IIR滤波器。
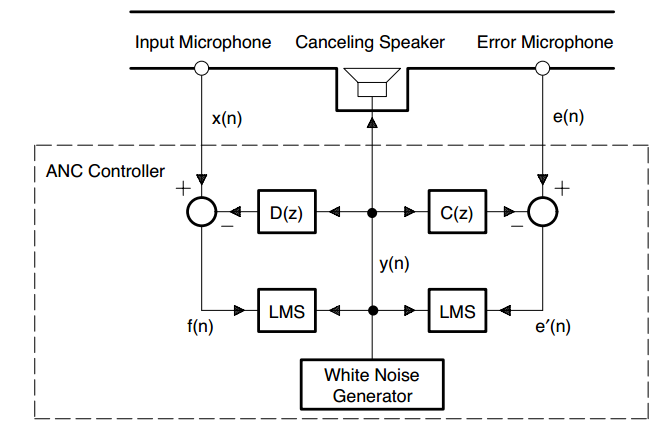
图5,FBFXLMS算法流程框图-离线计算$D(z)$和$C(z)$
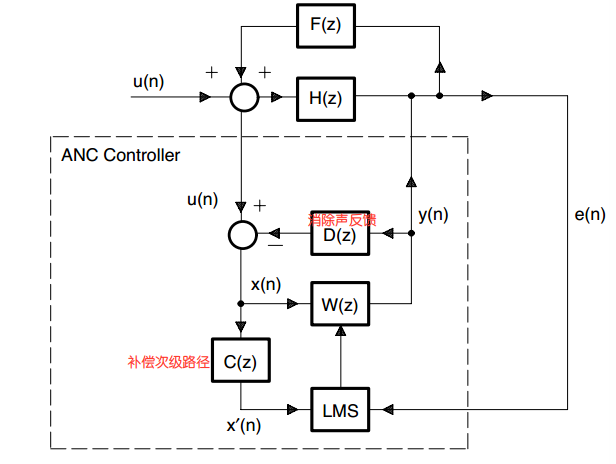
图6,FBFXLMS算法流程框图-在线更新滤波器$W(z)$
6、Filtered-U Recursive LMS(RLMS) Algorithm
自适应无限脉冲响应(IIR)滤波器将声学反馈作为整个声学装置的一部分,通过自适应IIR滤波器的极点来去除由声学反馈引入的极点。该算法在自适应消除过程中动态跟踪次要路径和反馈路径的变化。IIR滤波器输出结果为:\(y(n)=a^T(n)x(n)+b^T(n)y(n-1)\)
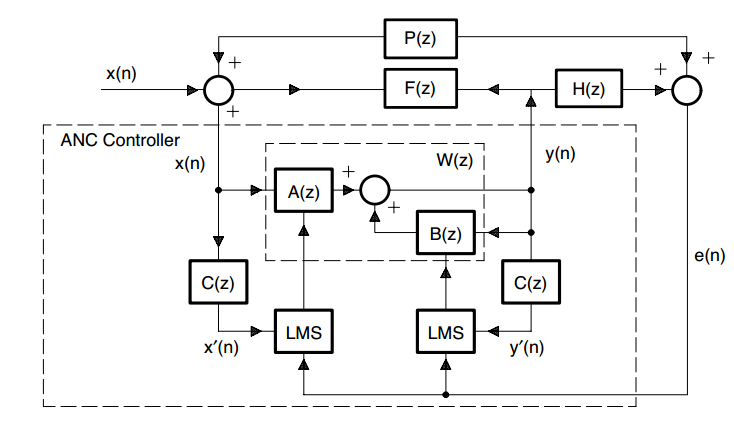
图7,Filtered-U RLMS算法流程框图
如果$A(z) B(z)$都收敛,$e(n)=0$,得到$\left\{\begin{matrix} X(z)P(z)+Y(z)F(z)P(z)+Y(z)H(z)=0 \\Y(z)=X(z)W(z) \end{matrix}\right.$
最后得到$W(z)=\frac{A(z)}{1-B(z)}=\frac{-P(z)}{H(z)-P(z)F(z)}$
文档上是上面公式,但自己推导符号不同,也一起写在这里吧$W(z)=\frac{A(z)}{1-B(z)}=\frac{-P(z)}{H(z)+P(z)F(z)}$
二、反馈ANC系统Feedback ANC Systems
反馈ANC系统只需要一个误差传声器,因此避免了前面讨论的双传声器前馈系统固有的声学反馈问题。反馈ANC方案依赖于具有周期性特征的信号。 主要噪声估计为:$x(n)=e(n)-\sum_{i=0}^{M-1}c_iy(n-i) $
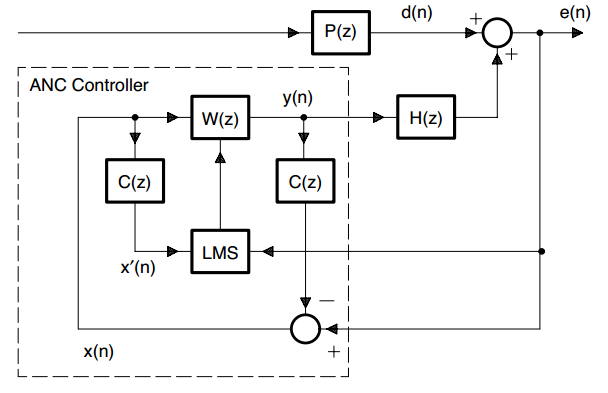
图8,反馈ANC算法流程框图
假设$W(z)$有足够的阶数,如果滤波器收敛,$E(z)=0$,得到
$X(z)W(z)H(z)=-D(z)$



 浙公网安备 33010602011771号
浙公网安备 33010602011771号