POJ 1003 -- Hangover

Hangover

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 126127		Accepted: 61563

Description

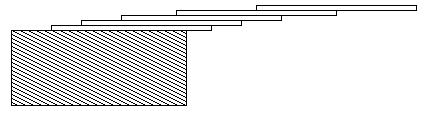
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.

Input

The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.

Output

For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.

Sample Input

1.00
3.71
0.04
5.19
0.00

Sample Output

3 card(s)
61 card(s)
1 card(s)
273 card(s)

Source

Mid-Central USA 2001

 

#include <iostream>
#include <cmath>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
using namespace std;
int main()
{
    double t;
    while(scanf("%lf",&t))   //*** 输入双精度浮点数：%lf *** 
    {
        if(t==0.00) break;
        double ans=0;
        for(int i=2;;i++)   //中间不写的话在循环中就一定要有退出条件 
        {
            ans+=1.0/(double)i;
            if(ans>=t)
            {
                printf("%d card(s)\n",i-1);
                break;
            }
        }
    }
    //system("pause");
    return 0;
}