栈

栈

、

1.超时

class Solution {
public:
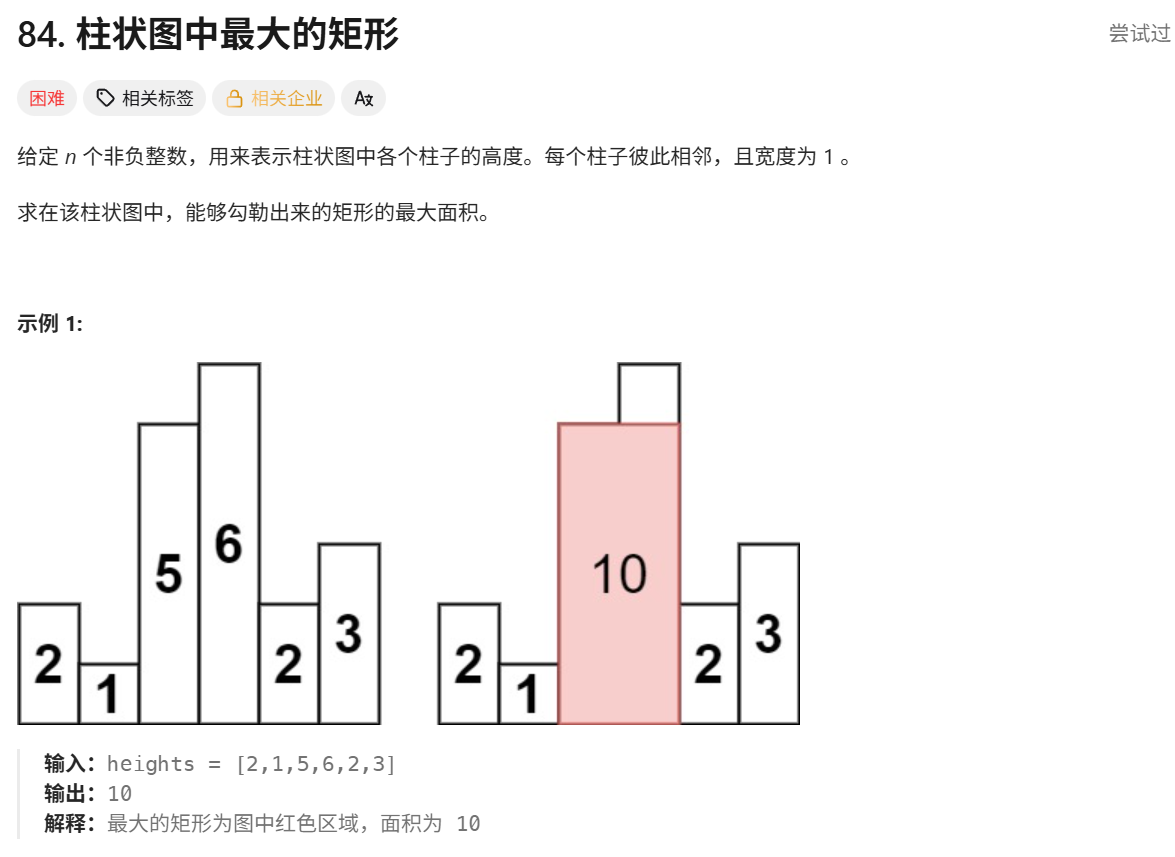
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        int ans = 0;
        // 枚举左边界
        for (int left = 0; left < n; ++left) {
            int minHeight = INT_MAX;
            // 枚举右边界
            for (int right = left; right < n; ++right) {
                // 确定高度
                minHeight = min(minHeight, heights[right]);
                // 计算面积
                ans = max(ans, (right - left + 1) * minHeight);
            }
        }
        return ans;
    }
};

2.

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n=heights.size();
       stack<int>st;//单调递减栈，栈顶最大(记录下标)
       vector<int>right(n);//right[i]记录从右到左一直高度小于等于当前高度heights[i]的右边界下标
       vector<int>left(n);//left[i]记录从左到右一直高度小于等于当前高度heights[i]的左边界下标
       int ans=0;
       for(int i=0;i<n;i++){
        while(!st.empty()&&heights[i]<=heights[st.top()]){//保证当前i这个地方高度最低（由于面积取决于min高度）
            st.pop();
        }
     if(!st.empty())  left[i]=st.top();
     else{
        left[i]=-1;
     }
            st.push(i);
       }
       st=stack<int>();
       for(int i=n-1;i>=0;i--){
            while(!st.empty()&&heights[i]<=heights[st.top()]){
                st.pop();
            }
  if(!st.empty())  right[i]=st.top();
     else{
        right[i]=n;
     }
            st.push(i);
       }

for(int i=0;i<n;i++){
    ans=max(ans,(right[i]-left[i]-1)*heights[i]);
}
        return ans;
    }
};