2025年11月24日

2025年11月24日

131题：分割回文串

class Solution {
private:
    vector<string>ans;//记录一组分割结果
    vector<vector<string>>ret;//记录返回结果，本题答案
    vector<vector<bool>>dp;//dp[i][j]记录子串s[i][j]是否是回文子串
    int n;
public:
    void dfs(string s,int i){
        if(i==n){
            ret.push_back(ans);
            return;
        }
        for(int j=i;j<n;j++){
            if(dp[i][j]==true){
               ans.push_back(s.substr(i, j - i + 1));
                dfs(s,j+1);
                ans.pop_back();
            }
        }
    }
   
    vector<vector<string>> partition(string s) {
        n=s.size();
        dp.assign(n,vector<bool>(n,true));//初始化dp全为true
        //判定子串是否为回文串
        for(int i=n-1;i>=0;i--){
            for(int j=i+1;j<n;j++){
                dp[i][j]=dp[i+1][j-1]&&(s[i]==s[j]);//因为要由串s[i+1][j-1]定s[i][j],所以i+1的位置要先确定，所以i倒着循环
            }
        }
        dfs(s,0);//分割点从0开始搜
        return ret;
    }
};

取子串s.substr(i, j - i + 1) 

155题：最小栈

方法一：辅助栈

class MinStack {
public:
    stack<int> x_stack;   // 存放所有输入数字的栈
    stack<int> min_stack; // 存放最小值的辅助栈
    MinStack() {
        // INT_MAX 的值为 2^31 - 1，固定值在c++里表示整数int最大值
        min_stack.push(INT_MAX); // 初始化辅助栈，将最大值放入辅助栈
    }


    void push(int val) {
        x_stack.push(val);
        min_stack.push(min(val, min_stack.top())); // 压入最小值栈（辅助栈）
    }


    void pop() {
        x_stack.pop();
        min_stack.pop();
    }


    int top() { return x_stack.top(); }//当前栈顶


    int getMin() { return min_stack.top(); }//最小值，最小值栈顶
};

方法二：差值栈

关键点：

• 创建一个栈维护元素与插入前栈元素最小值的差分，并维护当前栈最小值
• 注意防止 int 溢出(因为存放的是差值两个int一个最大int-一个最小的int一定超出int范围）

为了节省空间，使用一个差值栈

初始化：MinStack-->min_val=0

第一次输入元素：

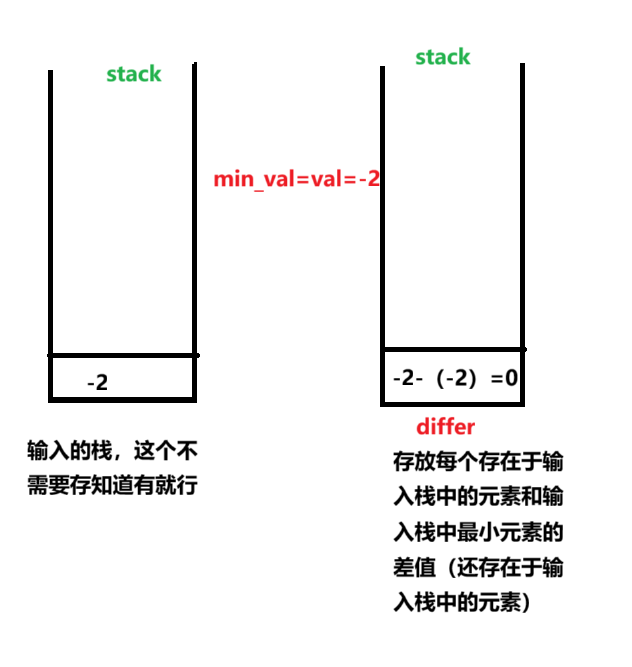
第二次插入0：

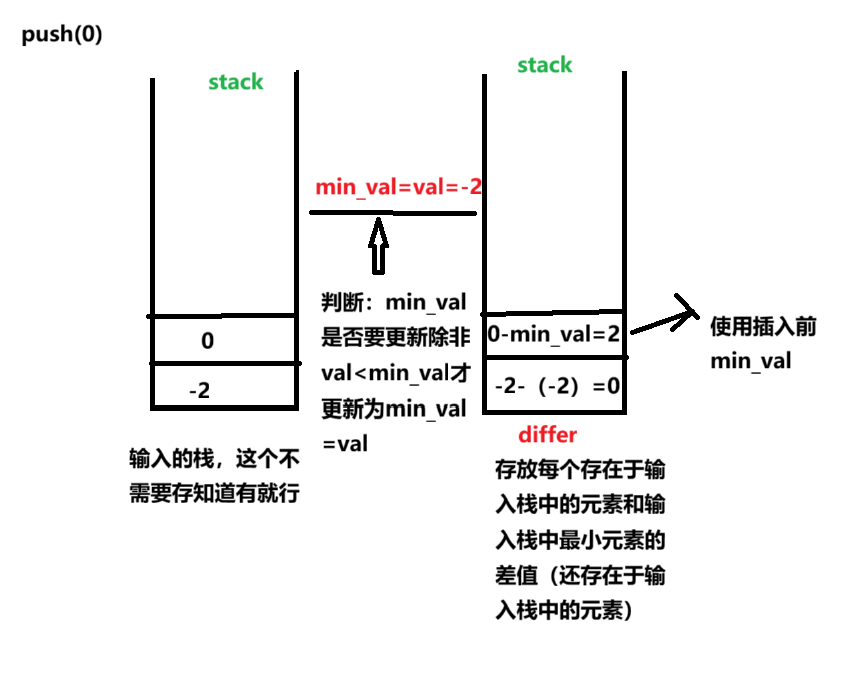
第三次插入-3

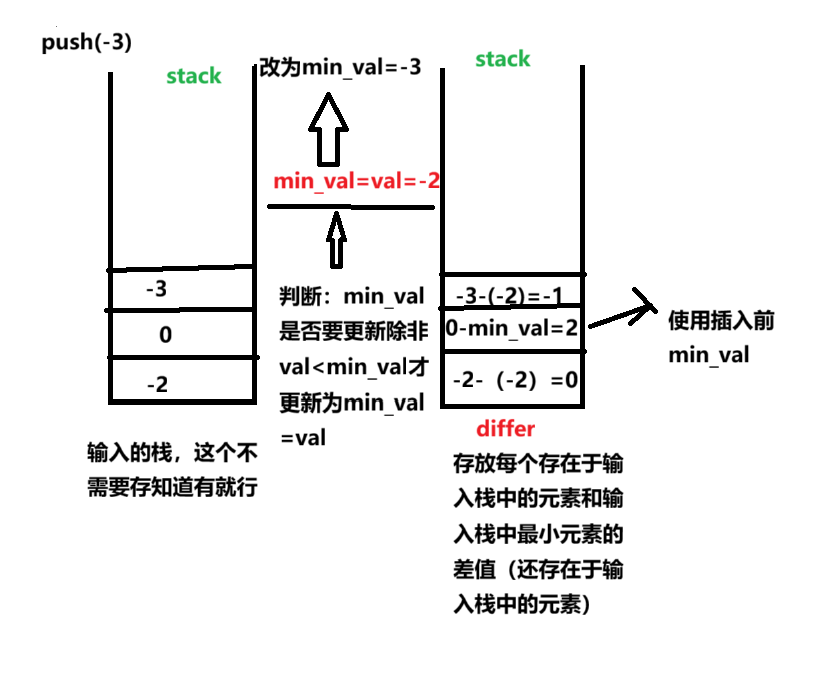
得到最小元素：getMin只需要返回min_val

第四次弹出栈顶元素：

min_val变成了-3-（-1）=-2

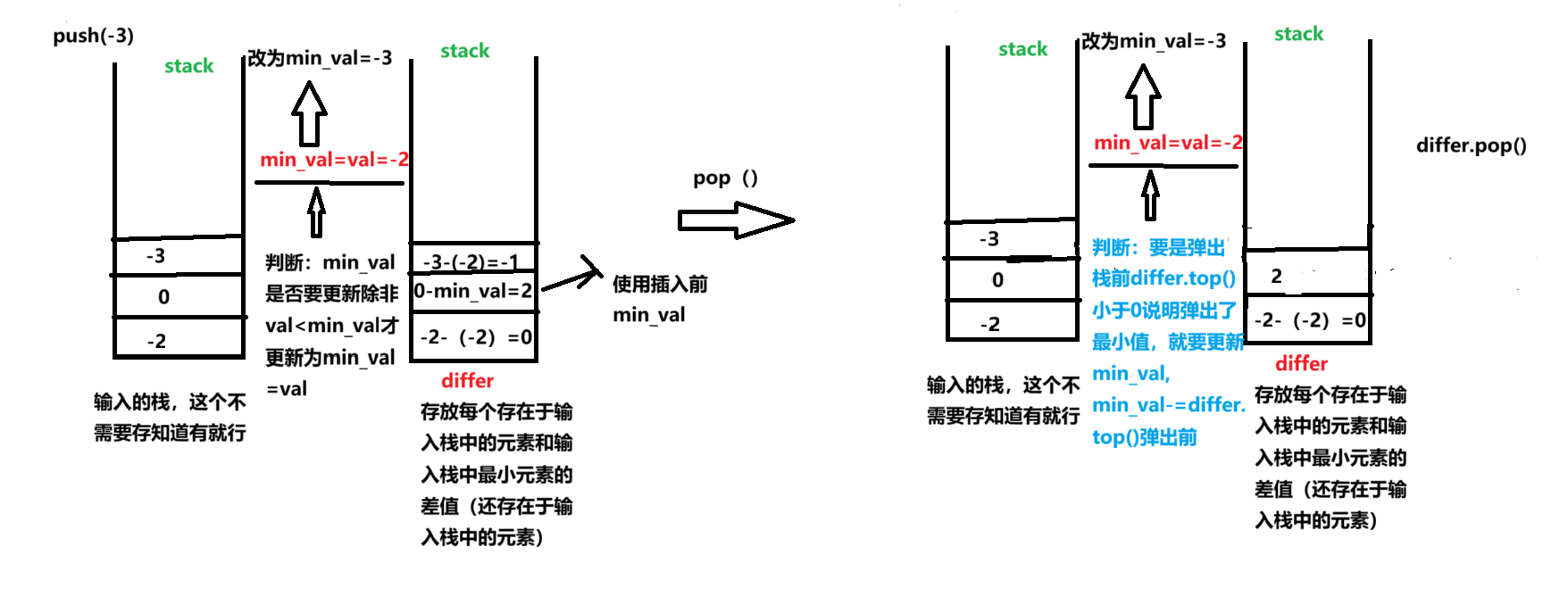
第五次得到输入栈的栈顶元素：返回2+（-2）=0；

 

 

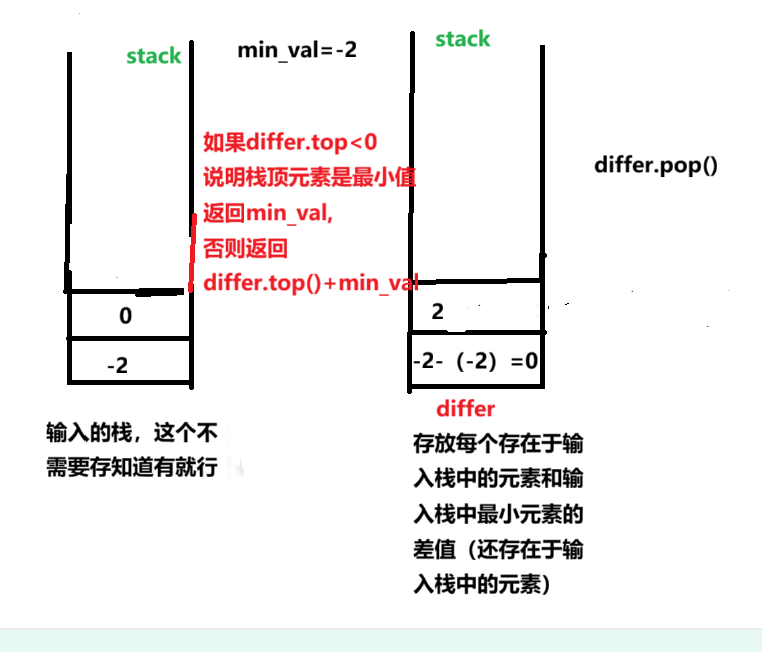
class MinStack {
    //为了节省辅助空间，只用一个栈-->差值栈
    stack<long long int>differ;//元素与最小元素值的差值
   long long  int min_val;//已输入元素且还存在未pop的元素中最小的元素值
public:
    MinStack() {
      min_val=0;
    }
    
    void push(int val) {
       if(differ.empty()==true){//刚输入
        min_val=val;
        differ.push(val-min_val);
       }
       else{
         differ.push(val-min_val);
      if(val<min_val)   min_val=val;
       }
    }
    
    void pop() {
       if(differ.top()<0) {//因为大于等于最小值的，插入差值栈的值都大于等于0
        min_val-=differ.top();
       }
        differ.pop();
    }
    
    int top() {
        if(differ.top()<0){
            return min_val;
        }
        else{
            return differ.top()+min_val;
        }
    }
    
    int getMin() {
        return min_val;
    }
};