动态规划
动态规划
70.爬楼梯

转换方程:dp[i]=dp[i-1]+dp[i-2] 思路:爬到第i节台阶前的前1节是一步或前两节是一步。

本题类似于斐波拉契数列
动态规划的方法利用的是数组比用递归函数时间复杂度好
class Solution {
public:
int climbStairs(int n) {
int dp[50];
dp[1]=1;
dp[2]=2;
for(int i=3;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
};118.杨辉三角

需要用二维数组存杨辉三角,而且要转化为直角三角形存储
由下图可得:转换方程dp[i][j]=dp[i-1][j-1]+dp[i-1][j]
dp表示当前位置的值
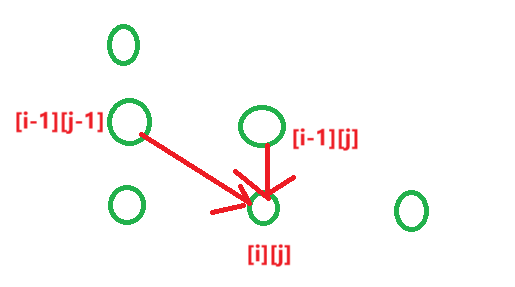
注意每行的两侧为1单列
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>>ans;
for(int i=0;i<numRows;i++){
vector<int>h;
h.push_back(1);
if(i>0){
for(int j=1;j<i;j++){
h.push_back(ans[i-1][j-1]+ans[i-1][j]);
}
h.push_back(1);
}
ans.push_back(h);
}
return ans; }
};198.打家劫舍

dp[i]表示前i个房子能抢到最大钱数
最后所求就是dp[房子数]
因为相邻的房子不可同时抢
所以转换方程:

思想有点像背包
dp[i]=max(dp[i-1],dp[i-2]+nums[i-1])//第i个房子不去抢dp[i-1],第i个房子要抢dp[i-2]+nums[i-1]。
class Solution {
public:
int rob(vector<int>& nums) {
int dp[130];//dp[i]表示取前i件的最高金额。
dp[0]=0;
dp[1]=nums[0];
for(int i=2;i<=nums.size();i++){
dp[i]=max(dp[i-1],dp[i-2]+nums[i-1]);
}
return dp[nums.size()];
}
};
下面几个题一个思路,将i拆分成j和i-j然后双循环
279.完全平方数

dp[i]表示i拆成的完全平方数数目最小数量。
转换方程:
i这个数可以拆分的完全平方数数目的最小值,可以用比他小的数转化而来
dp[i]=min(dp[i],dp[j]+dp[i-j])
将i这个数转成j和i-j
遍历比i小的所有数为j

class Solution {
public:
int numSquares(int n) {
int dp[10006];
memset(dp,10000,sizeof(dp));
dp[1]=1;
for(int i=2;i<=n;i++){
int k=(int)sqrt(i);
if(k*k==i){
dp[i]=1;
}
else{
for(int j=1;j<i;j++){
dp[i]=min(dp[i],dp[j]+dp[i-j]);
}
}
}
return dp[n];
}
};322.零钱兑换

dp[i]表示要凑到i元所需的最少硬币数
转换方程:
dp[i]=min(dp[i],dp[i-coins[j]]+1)//这个1表示用的coins[j]硬币
利用双循环:
i遍历1~amount元
j遍历coins里所有元素即拥有的硬币面值
将i元拆分成coins里有的硬币面值coins[j]且i>=coins[j] 和i-coins[j]元
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int dp[10006];
for(int i=0;i<10006;i++)dp[i]=10006;
dp[0]=0;
for(int i=1;i<=amount;i++){
for(int j=0;j<coins.size();j++){
if(i<coins[j])continue;
else{
dp[i]=min(dp[i],dp[i-coins[j]]+1);
}
}
}
if(dp[amount]>=10006)return -1;
else return dp[amount];
}
};139.单词拆分


字典worddict需要用set存放,因为要去重而且可以用find快速查找
思路:

dp[i]表示s串的前i个字符串是否可以用字典表示
所求:dp[s.size()]
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
set<string>st;//对字典进行去重,并且可用find进行快速查询是否存在某元素
for(auto i:wordDict){
st.insert(i);
}
bool dp[306];//dp[i]表示字符串s前i个字符串可以是否可以用字典里字符串搭配
fill(dp,dp+306,false);
dp[0]=true;//空字符串默认可搭配
for(int i=1;i<=s.size();i++){
for(int j=0;j<i;j++){
if(dp[j]&&st.find(s.substr(j,i-j))!=st.end()){
//dp[i] 看s的前i个字符可有字典搭配,i可拆成0~j-1,j~i,0~j-1可以用dp[j] 来判断,然后看s串种下标j~i 的字符串是否在字典中
dp[i]=true;
break;
}
}
}
return dp[s.size()];
}
};set插入因素用insert
查找用find,如果找不到返回集合名称.end()
如果s串的0~i-1可以在j处拆分则需要dp[j]=true并且set里有s的子串从下标j串长i-j
子串截取用substr(从哪个下标开始截取的,截取多长的)
优化版本:利用unordered_set这个是基于哈希表查询会更快
其次j不应该从0开始可以优化
首先计算字典中最长的词语长maxword
j从i-maxword
因为剩下部分i-j要从字典里找所以最长剩余部分长为maxword
所以优化后:
#include <vector>
#include <string>
#include <unordered_set>
#include <algorithm>
using namespace std;
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
// 1. 将字典转为哈希集合实现O(1)查询
unordered_set<string> words(wordDict.begin(), wordDict.end());
// 2. 计算字典中单词的最大长度(关键优化)
int maxLen = 0;
for (const string& word : wordDict) {
maxLen = max(maxLen, static_cast<int>(word.length()));
}
int n = s.length();
// 3. 定义动态规划数组
// dp[i]表示前i个字符(s[0..i-1])能否被字典单词拆分
vector<bool> dp(n + 1, false);
dp[0] = true; // 空字符串是可被拆分的(基础状态)
// 4. 状态转移过程
for (int i = 1; i <= n; i++) {
// 优化:只检查可能成为单词的长度范围
int start = max(0, i - maxLen);
for (int j = start; j < i; j++) {
// 状态转移条件检查:
// (1) 前j个字符是可拆分的(dp[j] == true)
// (2) 子串s[j..i-1]在字典中
if (dp[j] && words.find(s.substr(j, i - j)) != words.end()) {
dp[i] = true; // 满足条件则标记当前状态为true
break; // 找到一种可行方案即可跳出内层循环
}
}
}
return dp[n];
}
};300.最长递增子序列

暴力:动态规划
与上面类似双循环
dp[i]表示以原数组下标i的元素结尾的最长递增子序列的长度
然后遍历i之前比下标i对应元素小的值
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int dp[2510];
for(int i=0;i<2510;i++)dp[i]=1;
for(int i=1;i<nums.size();i++){
for(int j=i-1;j>=0;j--){
if(nums[i]>nums[j]) {
dp[i]=max(dp[i],dp[j]+1);
}
}
}
int ans=0;
for(int i=0;i<nums.size();i++)ans=max(ans,dp[i]);
return ans;
}
};优化:用二分lower——bound
利用一个数组end,end[i]记录递增序列长为i+1的最小结尾值
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int ans=0;
vector<int>end(nums.size());//end[i]表示长度为i+1的递增子序列结尾的最小值
for(int i=0;i<nums.size();i++){
int p=lower_bound(end.begin(),end.begin()+ans,nums[i])-end.begin();
if(p==ans)
{//找不到当前end数组里大于等于nums[i]的元素,所以放入end数组并且ans++
end[ans++]=nums[i];
}
else{//找到当前end数组里大于等于nums[i]的元素,替换从而来维护保存递增子序列结尾的最小值
end[p]=nums[i];
}
}
return ans;
}
};152.乘积最大子数组

因为有负数,所以得考虑可能当前元素是负数所以到当前元素结尾的最大乘积子数组可能是该元素前面选择的是乘积为最小负数*当前这个负的元素
所以需要维护最大乘积maxF,最小乘积minF(可能负)
直到当前元素结尾的最大乘积maxF是max(到前一个元素的maxF*当前元素,max(当前元素,minF*当前))//因为当前元素可能为负
直到当前元素结尾的最小乘积minF是min(到前一个元素的minF*当前元素,min(当前元素,maxF*当前))
class Solution {
public:
int maxProduct(vector<int>& nums) {
if(nums.size()==0)return 0;
if(nums.size()==1)return nums[0];
int maxF=nums[0];
int minF=nums[0];
int ans=nums[0];
for(int i=1;i<nums.size();i++){
int temp=maxF;
maxF=max(max(minF*nums[i],nums[i]),maxF*nums[i]);//因为要实现三者比较,所以两两先比,再将二者结果比
minF=min(min(temp*nums[i],nums[i]),minF*nums[i]);
ans=max(ans,maxF);
}
return ans;
}
};416.分割等和子集

解:
等和->说明要找的元素和确定
所以本题类似于背包(体积确定)
dp[i][j]表示前i+1个元素选取是否凑出可以凑出和为j
class Solution {
public:
bool canPartition(vector<int>& nums) {
if (nums.size() < 2) return false;
int total = 0;
int maxNum = nums[0];
for (int num : nums) {
total += num;
maxNum = max(maxNum, num);
}
if (total % 2 != 0) return false;
int target = total / 2;
if (maxNum > target) return false;
bool dp[202][10009];
for(int i=0;i<202;i++){
for(int j=0;j<10009;j++){
dp[i][j]=false;
}
}
dp[0][nums[0]] = true;
// 初始化第一列(和为0的情况,不选任何元素即可)
for (int i = 0; i < nums.size(); i++) {
dp[i][0] = true;
}
for (int i = 1; i < nums.size(); i++) {
for (int j = 1; j <= target; j++) {
if (j >= nums[i]) {
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[nums.size() - 1][target];
}
};32.最长有效括号

方法一:栈
括号匹配最先想到用栈
先压入-1(为了维护从下标0开始存)
遇到左括号就压入下标
遇到右括号,先弹出栈顶,然后要是栈为空就压入当前右括号下标,要是不为空,就用当前右括号下标减去栈顶元素的下标,并做比较取最大长度为有效最长序列
class Solution {
public:
int longestValidParentheses(string s) {
stack<int>st;
int ans=0;
st.push(-1);
for(int i=0;i<s.size();i++){
if(s[i]=='('){
st.push(i);
}
else{
st.pop();
if(st.empty()){
st.push(i);
}
else{
ans=max(ans,i-st.top());
}
}
}
return ans;
}
};方法二:
利用双指针,left统计左括号,right匹配右括号,从左到右扫一遍,再从右到左扫一遍
class Solution {
public:
int longestValidParentheses(string s) {
int left=0;
int right=0;
int ans=0;
for(int i=0;i<s.size();i++){
if(s[i]==')')right++;
else if(s[i]=='(')left++;
if(left==right)ans=max(ans,2*right);//匹配的
if(right>left){//不匹配时规0
left=0;
right=0;
}
}
left=0;
right=0;
for(int i=s.size()-1;i>=0;i--){
if(s[i]==')')right++;
else if(s[i]=='(')left++;
if(left==right)ans=max(ans,2*right);
if(left>right){
left=0;
right=0;
}
}
return ans;
}
};法三:动态规划
只有当前元素是)才考虑是否为有效序列结尾
dp[i]表示到下标为i的元素结尾时最长有序子序列长

class Solution {
public:
int longestValidParentheses(string s) {
const int N=3e4+9;
int dp[N];//dp[i]表示到s串中下标为i的字符时以这个位置结尾的最长有效子串长度
fill(dp,dp+N,0);
int ans=0;
for(int i=1;i<s.size();i++){
if(s[i]==')'){//有效的子串不可以以(结尾
if(s[i-1]=='('){//前一位和当前位构成()
if(i>=2) dp[i]=dp[i-2]+2;
else{
dp[i]=2;//下标为0单独处理
}
}
else if(i-dp[i-1]>0&&s[i-dp[i-1]-1]=='('){
if(i-dp[i-1]-2>=0) dp[i]=dp[i-1]+dp[i-dp[i-1]-2]+2;
else{
dp[i]=dp[i-1]+2;//下标为0单独处理
}
}
ans=max(ans,dp[i]);
}
}
return ans;
}
};




 浙公网安备 33010602011771号
浙公网安备 33010602011771号