42接雨水--双指针/动态规划/单调栈

42接雨水--双指针/动态规划/单调栈

题目：

分析

法一：动态规划

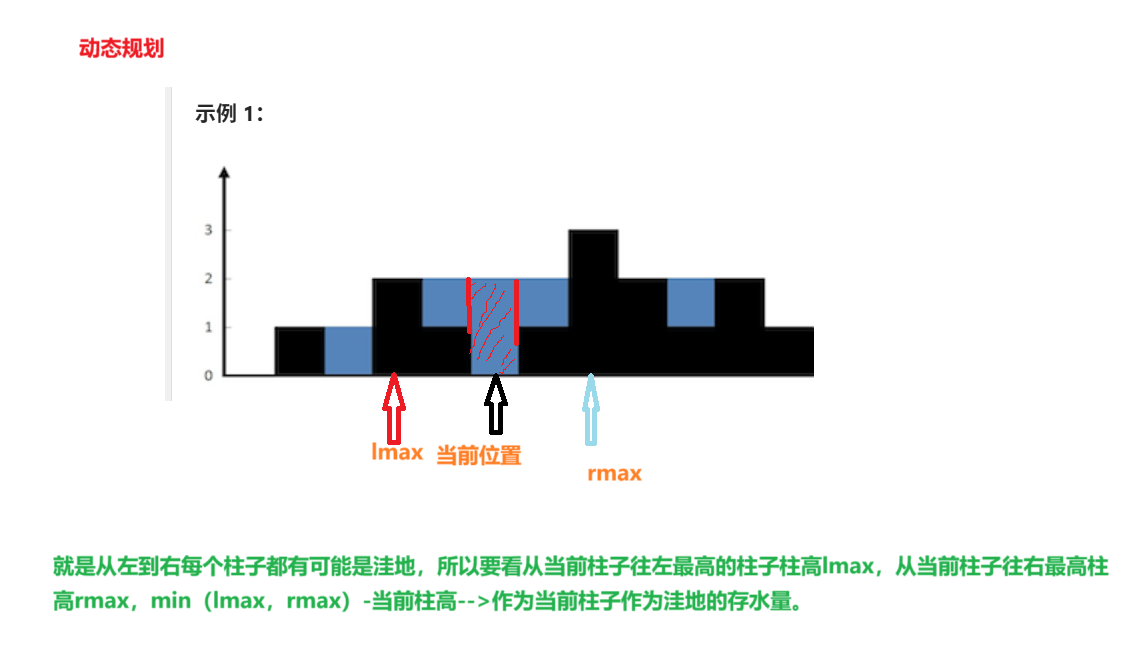
class Solution {
public:
    int trap(vector<int>& height) {
        int ans=0;
        int dlmax[20006];//从左往右到当前的柱子最高柱高
        int drmax[20006];//从右往左到当前的柱子最高柱高
        dlmax[0]=height[0];
        drmax[height.size()-1]=height[height.size()-1];
        //体现动态规划的思想
        for(int i=1;i<height.size();i++){
            dlmax[i]=max(height[i],dlmax[i-1]);
        }
        for(int i=height.size()-2;i>=0;i--){
            drmax[i]=max(height[i],drmax[i+1]);
        }
        for(int i=0;i<height.size();i++){
            ans=ans+min(dlmax[i],drmax[i])-height[i];
        }
        return ans;
    }
};

法二：双指针

左右指针，从两边向中间走
左右柱最终决定水深的是低的柱子
需要记录左柱最高高度和右柱最高高度
左指针l=0
右指针r=size-1
左柱最高高度lmax
右柱最高高度rmax
初始lmax=0，rmax=0
从左往右如果h[l]>lmax更新lmax=h[l]，否则左柱最高大于目前柱所以是个洼地能存水
这个洼地存水=lmax-h[l]
从右往左如果h[r]>rmax更新rmax=h[r]，否则右柱最高大于目前柱所以是个洼地能存水
这个洼地存水=rmax-h[r]

class Solution {
public:
    int trap(vector<int>& height) {
        int l=0;
        int r=height.size()-1;
        int lmax=0;
        int rmax=0;
        int ans=0;
        while(l<r){
            if(height[l]<height[r]){
            //左柱低
            if(height[l]>lmax){
                lmax=height[l];
            }
            else{
                //洼地
                ans=ans+lmax-height[l];
            }
            l++;
            }
            else{
                if(height[r]>rmax){
                    rmax=height[r];
                }
                else{
//洼地
                    ans=ans+rmax-height[r];
                }
                r--;
            }
        }
       return ans; 
    }
};

法三：单调栈

本题为：栈顶到栈底单调递减栈，栈顶最小

class Solution {
public:
    int trap(vector<int>& height) {
        /*
单调栈：本题目把比栈顶小的柱子高度对应的下标压栈
碰到比栈顶高的柱子：就弹出栈顶说明栈顶位置为低洼，栈顶下面那个元素柱的高度大于栈顶柱子高
所以他下面的元素和当前元素就是栈顶左右边
栈顶洼地：宽度=当前位置-栈顶下面元素下标-1
高度=min（当前位置柱高，栈顶下面元素对应柱高）-栈顶柱高
ans=ans+宽度*高度
        */
        int i = 0;
        int ans = 0;
        stack<int> a;//注意：栈内存柱子下标
        while (i < height.size()) { // 从左往右遍历所有的柱子

            while (!a.empty() && height[i] >height[ a.top()]) {
                int b = a.top();
                a.pop();
               if(a.empty()){//当栈为空的时候要退出循环因为没法a.top()
                break;
               }
                int wid = i - a.top() - 1;
                int h = min(height[i], height[a.top()]) - height[b];
                ans = ans + wid * h;
            }
            a.push(i);
            i++;
        }
        return ans;
    }
};