dfs

dfs深度优先遍历

一般思路：遍历所有情况，从第一层一直往下，搜到最后一层再回溯到上一层，为防止重复搜一般可能会用bool数组记录一下访问过没，

如果没访问过：

记录已经访问->dfs（下一层）->修改成没访问过

1.数字排列

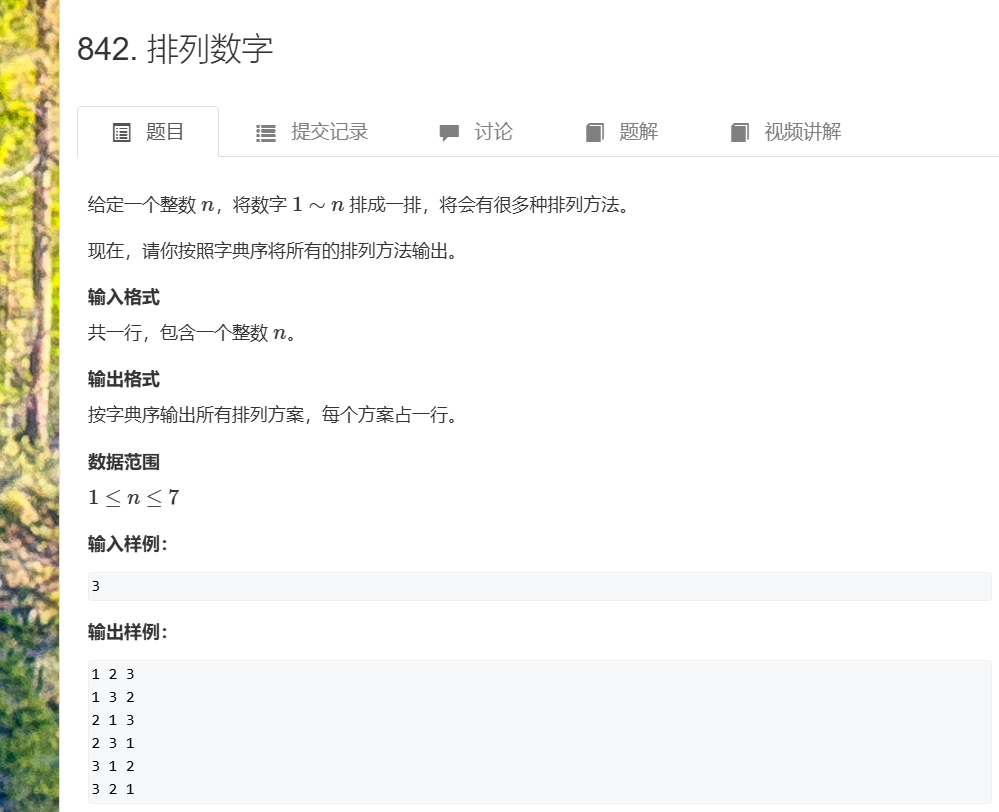
#include<bits/stdc++.h>
using namespace std;
int n;
char path[10];
bool flag[10];
void dfs(int dep){//dep为层
    if(dep==n+1){
     for(int i=1;i<=n;i++){
         cout<<path[i]<<" ";
     }
     cout<<endl;
     return;
    }
    for(int i=1;i<=n;i++){
     if(flag[i]) {
         continue;
     }  
     flag[i]=true;
     path[dep]=i;
     dfs(dep+1);
     flag[i]=false;
    }
}
int main(){
cin>>n;
dfs(1);
return 0;
}

2.n皇后

不同行：一维数组

不同列：之前层没有经过这列

不同斜线：是指每条平行的对角线上只能有一个皇后

即：这样也不可以！

Q
		Q

解法一：

/*n皇后问题：dfs问题 
1.path[i]记录第i行的Q在path[i]列（解决了不同行问题） 
*/ 
#include<bits/stdc++.h> 
using namespace std;
int n;
int path[20];
void dfs(int dep){
	if(dep==n+1){//递归出口 
		for(int i=1;i<=n;i++){//行 
			for(int j=1;j<=n;j++) {//列 
				if(j==path[i]){
					cout<<"Q";
				}
				else{
					cout<<".";
				}
			}
			cout<<endl; 
		}
		cout<<endl;
		return;
	}
	for(int i=1;i<=n;i++){
		bool flag=true; 
		for(int j=1;j<dep;j++){
			if(i==path[j]||abs(dep-j)==abs(i-path[j])){
			flag=false;
			break;
			}
		}
		if(flag==false){
			continue;
		}
		path[dep]=i;
		dfs(dep+1);
		//path[dep]=0;反正每次都赋予新值，所以不用恢复
	}
}
int main(){
	cin>>n;
	dfs(1);
	return 0;
}

解法二：

升级版（时间复杂度更好）

 

/*n皇后问题：dfs问题 
1.path[i]记录第i行的Q在path[i]列（解决了不同行问题） 
*/ 
#include<bits/stdc++.h> 
using namespace std;
int n;
int path[20];
bool col[20];//列是否经过
bool dj[40];//正对角线是否经过
bool fdj[40];//反对角线是否经过 
void dfs(int dep){
	if(dep==n+1){//递归出口 
		for(int i=1;i<=n;i++){//行 
			for(int j=1;j<=n;j++) {//列 
				if(j==path[i]){
					cout<<"Q";
				}
				else{
					cout<<".";
				}
			}
			cout<<endl; 
		}
		cout<<endl;
		return;
	}
	for(int i=1;i<=n;i++){
	if(!col[i]&&!dj[dep-i+n]&&!fdj[dep+i]) {
		col[i]=true;//列
		dj[dep-i+n]=true;//对角线截距b=y-x为了防止<0所以+n
		fdj[dep+i]=true;//反对角线b=y+x
		path[dep]=i;
		dfs(dep+1);
		col[i]=false;
		dj[dep-i+n]=false;
		fdj[dep+i]=false;
	}
	}
}
int main(){
	cin>>n;
	dfs(1);
	return 0;
}

3.树的重心

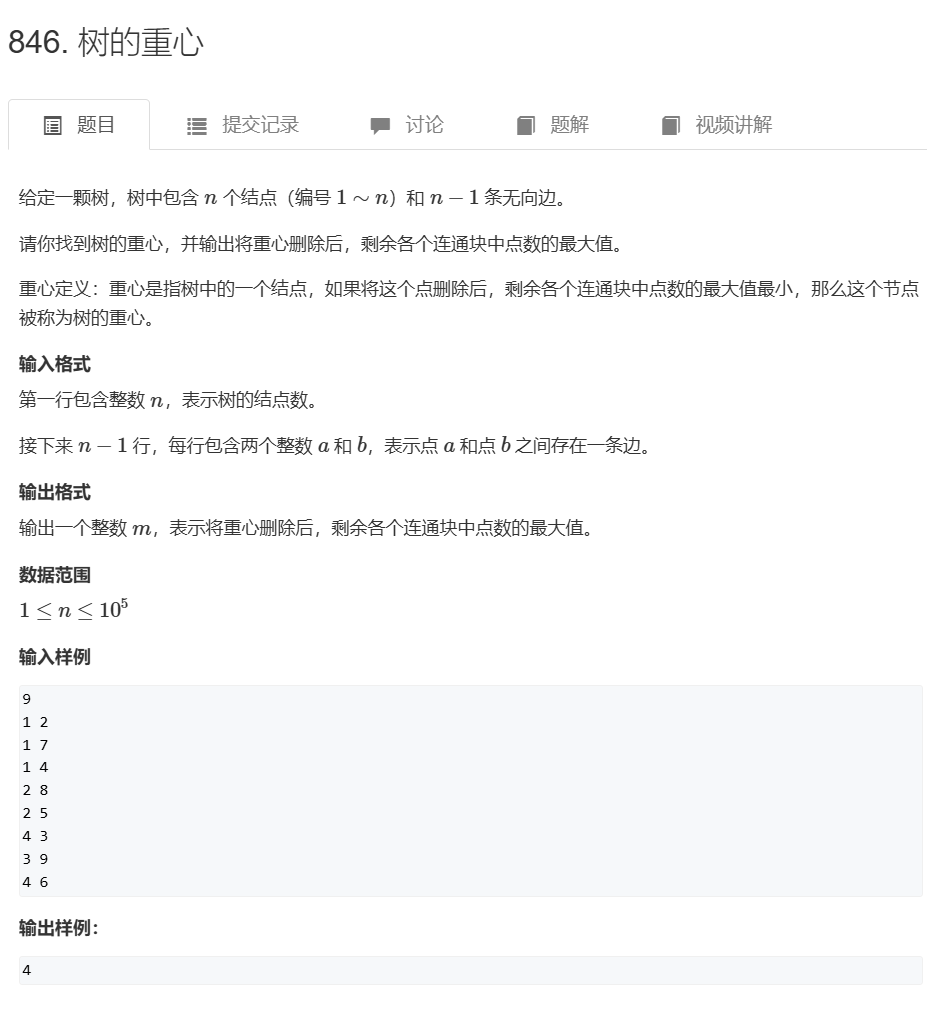
#include<bits/stdc++.h> 
using namespace std;
const int N=1e5+6;
const int M=2*N;
int h[N];
int e[M];
int ne[M];
int idx;
int n;
int ans=N; 
bool st[N];//是否搜过该根节点 
//邻接表存图 
void add(int a,int b) {
	e[idx]=b;
	ne[idx]=h[a];
	h[a]=idx++;
}
//dfs来计算指定根结点树的大小 
int dfs(int u) {
	st[u] =true;
	int sum=1;//先放入根u 
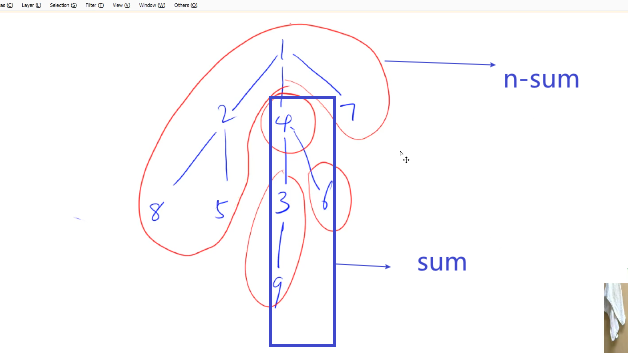
	int l=0;//连通块最大值
    //删除一个点后，连通块包含他的各个子树，以及n-sum
    
	//u的相邻结点（子节点） 
	for(int i=h[u];i!=-1;i=ne[i]){
		int j=e[i];
		if(!st[j]){//没有搜过该结点 
			int s=dfs(j);
			l=max(l,s);
			 sum+=s;
		}
	}
	l=max(l,n-sum);
	ans=min(ans,l);
	return sum;
}
int main(){
	memset(h,-1,sizeof(h));
	cin>>n;
	int a,b;
	for(int i=1;i<n;i++){
		cin>>a>>b;
		add(a,b);
		add(b,a);
	}
	dfs(1);//从第一个点开始搜 
	cout<<ans;
	return 0;
}