第十五届蓝桥杯省赛
第十五届蓝桥杯省赛
1.握手问题
#include <iostream>
using namespace std;
int main()
{
//划分为43,7两组
//(43*42)/2+7*43=28*43
cout<<28*43;
return 0;
}
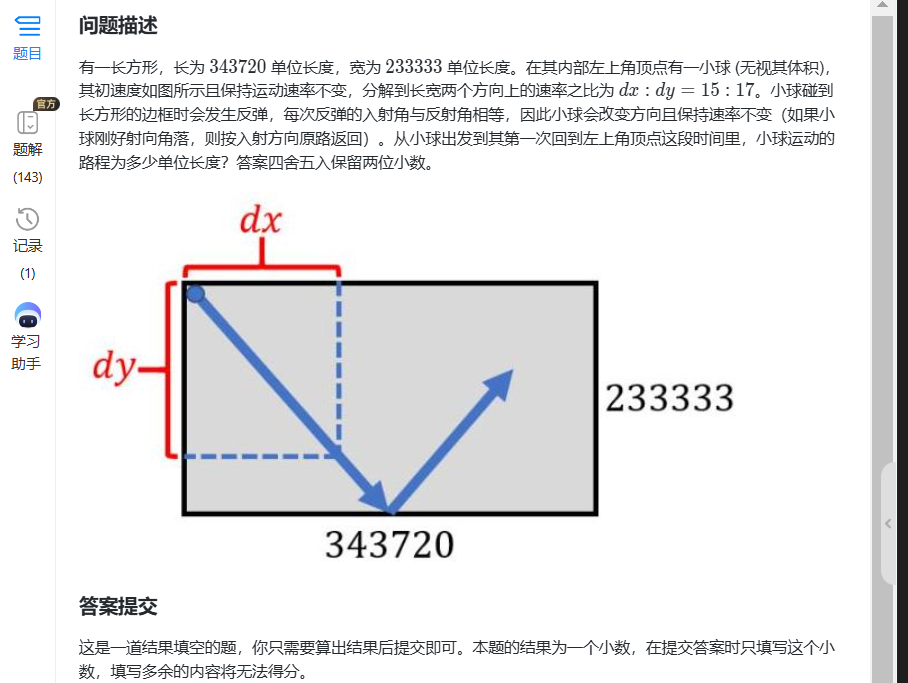
2.小球反弹（难）
分析：
当做两个方向往返
代码：
/*
考点：速度分解
分解为x轴往返，y轴往返（回到左上角起点）
假设x轴做了p个往返，y轴做了q个往返，时间为t
速度可以当做是x轴15，y轴17
x轴路程：dx*t=p*2*x
y轴路程：dy*t=q*2*y
两式相除
dx/dy=p/q*x/y
即(dx*y)/(dy*x)=p/q
可以把分子看作p，分母看作q (因为不想算除法)
p,q需要约分通过gcd找最大公约数约分-->因为是第一次到达时间要最小！
由p求t->t=2px/dx
*/
#include<bits/stdc++.h>
using namespace std;
int gcd(int p,int q){
if(q==0){
return p;
}
else{
return gcd(q,p%q);
}
}
int main(){
int x=343720;
int y=233333;
int dx=15;
int dy=17;
int p=dx*y;
int q=dy*x;
int g=gcd(p,q);//g为p,q的最大公约数
p=p/g;
q=q/g;
double t=p*2*x/dx;//时间
double s=t*sqrt(15*15+17*17);//总路程
printf("%.2f",s);
return 0;
}核心：(dx*y)/(dy*x)=p/q
需要记忆的模版（最大公约数）gcd
int gcd(int p,int q){
if(q==0){
return p;
}
else{
return gcd(q,p%q);
}
}3.好数
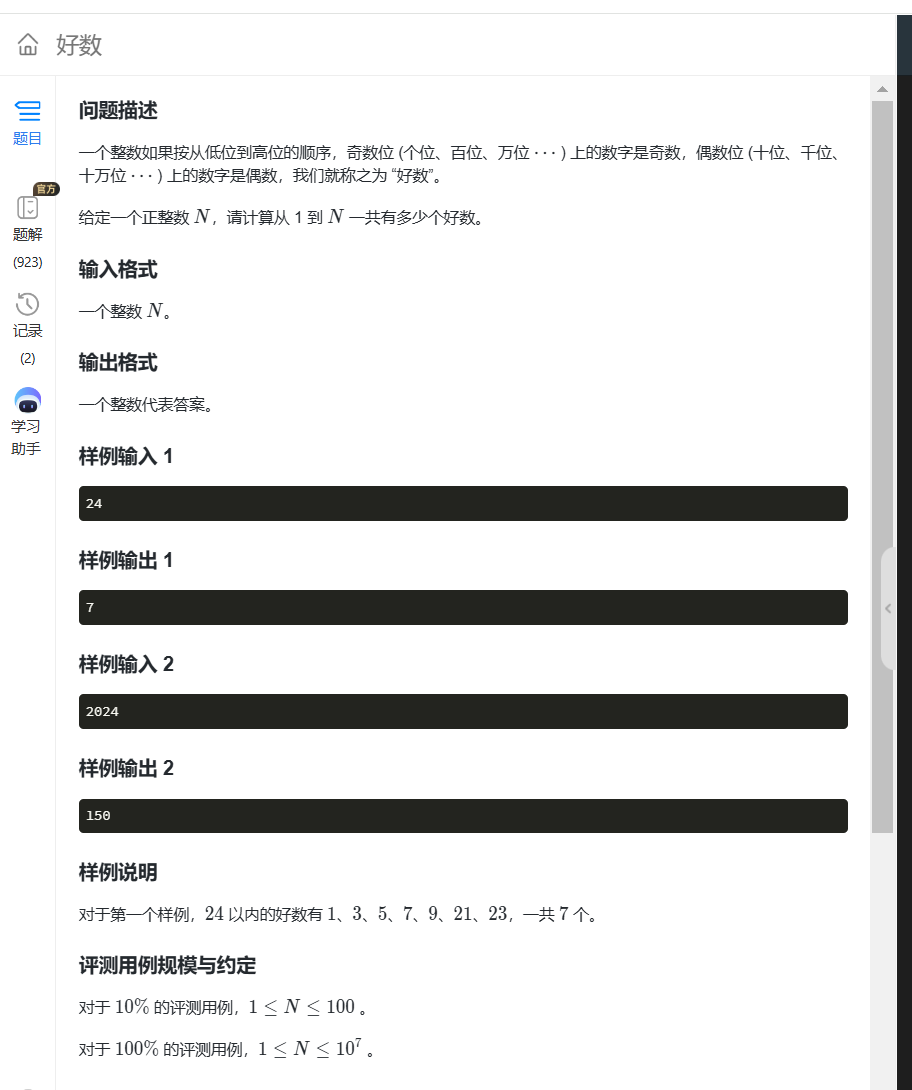
//考察取每一位
#include<bits/stdc++.h>
using namespace std;
bool good(int a){//如果是好数返回true
int i=0;
while(a!=0){
i++;
int d=a%10;//当前位的数字
if(i%2!=0){//奇数位
if(d%2==0){
return false;
}
}
else if(i%2==0){//偶数位
if(d%2!=0){
return false;
}
}
a/=10;
}
return true;
}
int main(){
int n;
cin>>n;
int cnt=0;
for(int i=1;i<=n;i++){
if(good(i)){
// cout<<i<<endl;
cnt++;
}
}
// cout<<"------------------------------------------";
cout<<cnt;
return 0;
}4.R格式（难）
考点：高精度*低精度
答案代码
/*
分析：
求2^n*d
2的n次方当n为1000时非常大所以要用高精度算法
d很小为低精度
所以本题考：高精度*低精度
高精度可以用数组模拟
*/
#include<bits/stdc++.h>
using namespace std;
const int N=1300;
int a[N];//将字符串每一位转为整型 -->数组不开成全局变量而且不初始化可能会有脏数据
string s;//存放低精度浮点数
int main(){
int n;
cin>>n>>s;
reverse(s.begin(),s.end());//高精度算法因为可能涉及进位，所以先把字符串翻转，则原来的最高位进位变成现在往右增加一位
int pos=s.find('.');//小数点位置
s.erase(pos,1);//删除小数点，因为本题最后四舍五入与小数点无关。从pos开始删一位就是把小数点删除了
int len=s.size();
//字符串转整型
for(int i=0;i<len;i++){
a[i+1]=s[i]-'0';
}
//乘n个2
for(int i=0;i<n;i++){
//每一位乘2
//扫描
for(int j=1;j<=len;j++){
a[j]*=2;
}
//处理进位问题
for(int j=1;j<=len;j++){
if(a[j]>=10){
a[j+1]++;
a[j]%=10;
if(j==len){//最高位
len++;
}
}
}
}
//小数点四舍五入
if(a[pos]>=5){
a[pos+1]++;
//四舍五入后进位问题
for(int i=pos+1;i<=len;i++){
if(a[i]>=10){
a[i+1]++;
a[i]%=10;
if(i==len){
len++;
}
}
}
}
//反着输出
for(int i=len;i>=pos+1;i--){
cout<<a[i];
}
return 0;
}分析代码
/*
分析：
求2^n*d
2的n次方当n为1000时非常大所以要用高精度算法
d很小为低精度
所以本题考：高精度*低精度
高精度可以用数组模拟
*/
#include<bits/stdc++.h>
using namespace std;
const int N=1300;
int a[N];//将字符串每一位转为整型
string s;//存放低精度浮点数
int main(){
int n;
cin>>n>>s;//s就是d
reverse(s.begin(),s.end());//高精度算法因为可能涉及进位，所以先把字符串翻转，则原来的最高位进位变成现在往右增加一位
//find,erase，size是字符串方法
int pos=s.find('.');//小数点位置
s.erase(pos,1);//删除小数点，因为本题最后四舍五入与小数点无关。从pos开始删一位就是把小数点删除了
int len=s.size();//删完后字符串s长度
//字符串转整型
for(int i=0;i<len;i++){//a数组从下标1开始存放
a[i+1]=s[i]-'0';//字符串转整型
}
//乘n个2
for(int i=0;i<n;i++){//n个2相乘
//每一位乘2
//扫描
for(int j=1;j<=len;j++){//遍历a
a[j]*=2;
}
//处理进位问题
for(int j=1;j<=len;j++){//遍历a
if(a[j]>=10){
a[j+1]++;
a[j]%=10;
if(j==len){//最高位，并且最高位>=10要进位
len++;
}
}
}
}
//小数点四舍五入
if(a[pos]>=5){
a[pos+1]++;
//四舍五入后进位问题
for(int i=pos+1;i<=len;i++){
if(a[i]>=10){
a[i+1]++;
a[i]%=10;
if(i==len){
len++;
}
}
}
}
//反着输出（从高位->低位输出）
for(int i=len;i>=pos+1;i--){
cout<<a[i];
}
return 0;
}
删除小数点后
5.宝石组合（难）
考点：唯一分解定理
代码：
/*
分析：
考点：唯一分解定理
任何一个大于1的自然数，如果他不是质数，那么他可以分解为有限个质数的乘积
例如：A,B为两个大于1的自然数
A=p1^a1*p2^a2*p3^a3*...pn^an
B=p1^b1*p2^b2*p3^b3*...pn^bn
p1,p2...pn为质数
a1~an,b1~bn为指数
最大公因数:gcd(A,B)=p1^min(a1,b1)*p2^min(a2,b2)*...*pn^min(an,bn)
最小公倍数:lcm(A,B)=p1^max(a1,b1)*p2^max(a2,b2)*...*pn^max(an,bn)
由此可得
假设a,b,c的公共质因子(底数)的指数分别为x,y,z
则(乘相当于指数相加，除相当于指数相减)
s可以看做x+y+z+max(x,y,z)-max(x,y)-max(x,z)-max(y,z)->答案应该是x,y,z中一个数
所以为使得s最大则只需要找到最大公约数
*/
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+6;
int a[N];
vector<int>fac[N];//存放每个数的因子。因为因子是不断放进来所以用动态数组vector，fac[i][j]表示i的第j个因子
vector<int>s[N];//s[i][j]表示i的第j个倍数，i为因子s[i]是找出以i为因子的所有数组成的数组
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
//因为要输出字典序最小，所以先对a从小到大排序
sort(a+1,a+1+n);
//求每个数字的因子
for(int i=1;i<=1e5;i++){
for(int j=i;j<=1e5;j+=i){
//j为i的倍数
fac[j].push_back(i);//i是j的因子
}
}
//求各因子对应的倍数（倍数是a数组里的数）
for(int i=1;i<=n;i++){//遍历a数组，求a数组里每个数的所有因子对应的a数组的数
for(int j=0;j<fac[a[i]].size();j++){
s[fac[a[i]][j]].push_back(a[i]);//表示a[i]的第j个因子对应的倍数有a[i]
}
}
//输出最大因子对应的三个倍数
for(int i=1e5;i>=1;i--)
{
if(s[i].size()>=3){
cout<<s[i][0]<<" "<<s[i][1]<<" "<<s[i][2];
return 0;
}
}
return 0;
}6.爬山
考点：优先队列（堆）
贪心思想：
每次对最大的那个数字操作-->大根堆（也就是优先队列的默认）
开根号比除以2减小的更快
代码：
//考点是优先队列（默认大根堆）
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,p,q;
cin>>n>>p>>q;
priority_queue<int,vector<int> >d;//vector<int>后面需要有个空格
int h;
for(int i=0;i<n;i++){
cin>>h;
d.push(h);
}
for(int i=0;i<p;i++){
int a=d.top();
a=sqrt(a);
d.pop();
d.push(a);
}
for(int i=0;i<q;i++){
int a=d.top();
a/=2;
d.pop();
d.push(a);
}
long long int sum=0;
for(int i=0;i<n;i++){
sum+=d.top();
d.pop();
}
cout<<sum;
return 0;
}堆总结
c++里堆用priority_queue写
堆操作：
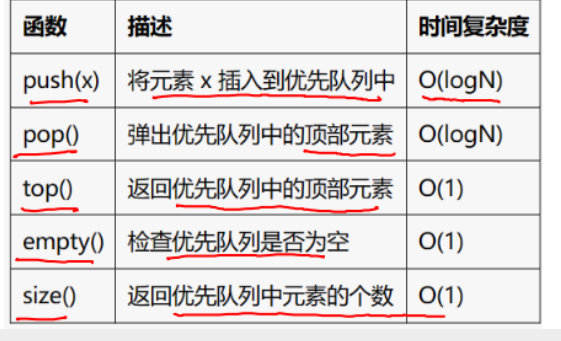
默认是大根堆，堆顶最大
大根堆写法：
priority_queue<int,vector<int> >
小根堆：
priority_queue<int,vector<int>,greater<int> >q;
自定义堆：
用结构体struct自定义堆
例如：下面自定义的小根堆
//自定义堆
#include<bits/stdc++.h>
using namespace std;
struct Com{
bool operator()(int a,int b){
return a>b;
}
};
int main(){
int n;
cin>>n;
priority_queue<int,vector<int>,Com >q;
for(int i=0;i<n;i++)
{
int a;
cin>>a;
q.push(a);
}
return 0;
}
说明这个结构体定义的是小根堆，数字越小优先级越高
8.拔河（非常难做）
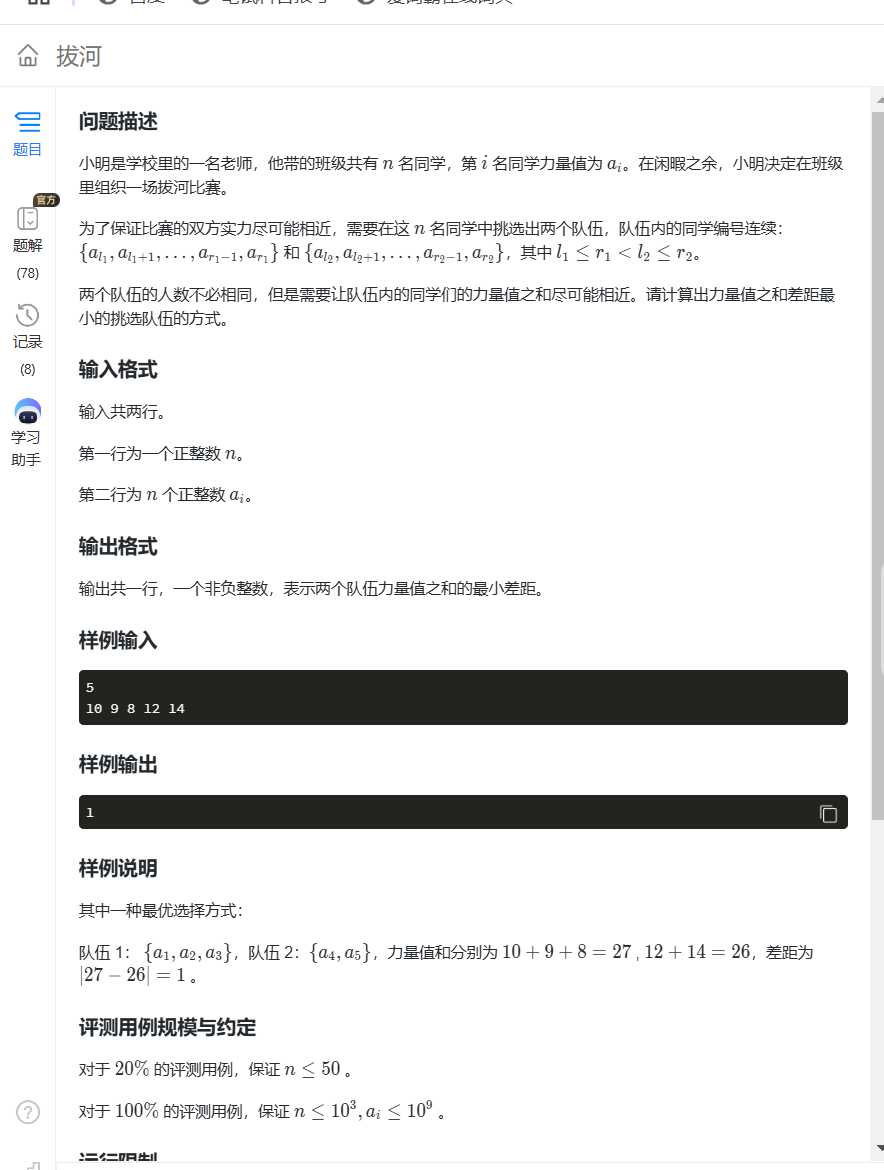
暴力（四种循环，20%）
#include <iostream>
using namespace std;
long long int a[1003];
long long int ans;
long long int s(int l,int r){
long long int sum=0;
for(int i=l;i<=r;i++){
sum+=a[i];
}
return sum;
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
ans+=a[i];
}
for(int l1=1;l1<n;l1++){
for(int r1=l1;r1<n;r1++){
for(int l2=r1+1;l2<=n;l2++){
for(int r2=l2;r2<=n;r2++){
long long int z=s(l1,r1);
long long int y= s(l2,r2);
ans=min(ans,abs(z-y));
}
}
}
}
cout<<ans;
return 0;
}前缀和改进 得40%分：
#include <bits/stdc++.h>
using namespace std;
long long int s[1003];
long long int d[1003][1003];
long long int ans;
int main()
{
int n;
cin>>n;
int a;
for(int i=1;i<=n;i++){
cin>>a;
ans+=a;
s[i]=s[i-1]+a;
}
for(int i=1;i<=n;i++){
for(int j=i;j<=n;j++){
d[i][j]=s[j]-s[i-1];
}
}
for(int l1=1;l1<n;l1++){
for(int r1=l1;r1<n;r1++){
for(int l2=r1+1;l2<=n;l2++){
for(int r2=l2;r2<=n;r2++){
long long int z=d[l1][r1];
long long int y= d[l2][r2];
ans=min(ans,abs(z-y));
}
}
}
}
cout<<ans;
return 0;
}
正解： 前缀和+multiset+lowerbound（100%）
完整的代码：
/*
分析：
考察：
1.区间和-->前缀和算法
2.最接近-->二分算法（可以用lowerbound解决），所以可以用multiset存储区间和，multiset自带lower_bound
multiset是可含重复元素的集合，并且默认升序排列，可以使用lowerbound，upper_bound
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const int N=1e3+6;
ll a[N];//原数列
ll s[N];//从头开始，前缀和
multiset<ll>m;//存区间和
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
//前缀和
for(int i=1;i<=n;i++){
s[i]=s[i-1]+a[i];
}
// //区间和(可以求得所有区间和)
// for(int i=1;i<=n;i++){
// for(int j=1;j<=i;j++){
// //计算区间[j,i]的和
// ll h=s[i]-s[j-1];
// m.insert(h);
// }
// }
ll ans=1e9;//先放最大
//求解答案（做减法）
for(int l=1;l<=n;l++){
for(int j=1;j<l;j++){//第一个区间用multiset维护
m.insert(s[l-1]-s[j-1]);
}
for(int r=l;r<=n;r++){
//sum为区间[l,r]的和(第二个区间)
ll sum=s[r]-s[l-1];//取出一个区间
//利用lowerbound找与他最接近的区间和
auto t=m.lower_bound(sum);//lowerbound返回第一个大于等于他的数的迭代器
if(t!=m.end()){//表示存在大于等于他的数
ans=min(ans,abs(*t-sum));
}
if(t!=m.begin()){//比他小的，要判断t可以往前一位因为怕multiset里就一个元素向前一位就空
t--;
ans=min(ans,abs(*t-sum));
}
}
}
cout<<ans;
return 0;
}核心代码解释：
（1）碰见区间求和要想到用前缀和的办法
前缀和模版
//前缀和（即区间[1,i]和）
for(int i=1;i<=n;i++){
s[i]=s[i-1]+a[i];
}
（2）两个区间和计算，找最小差值
ll ans=1e9;//先放最大
//求解答案（做减法）
for(int l=1;l<=n;l++){
for(int j=1;j<l;j++){//第一个区间用multiset维护
m.insert(s[l-1]-s[j-1]);
}
for(int r=l;r<=n;r++){
//sum为区间[l,r]的和(第二个区间)
ll sum=s[r]-s[l-1];//取出一个区间
//利用lowerbound找与他最接近的区间和
auto t=m.lower_bound(sum);//lowerbound返回第一个大于等于他的数的迭代器
if(t!=m.end()){//表示存在大于等于他的数
ans=min(ans,abs(*t-sum));
}
if(t!=m.begin()){//比他小的
t--;
ans=min(ans,abs(*t-sum));
}
}
}
cout<<ans;
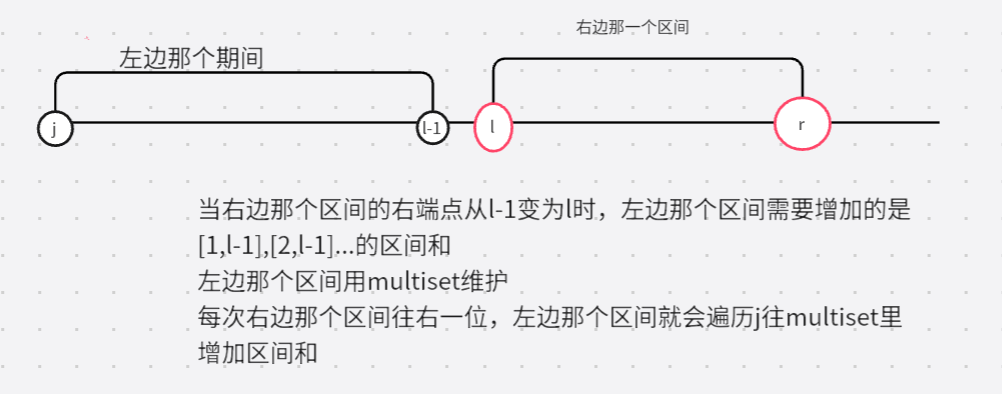
lowerbound在这道题的作用：
先取出一个右边区间的和，然后在左边找一个最接近他的区间和，左边各区间和用multiset维护，找寻第一个大于等于他的数用lowerbound，返回迭代器。
然后也可能左边区间和比他小的那个作差绝对值更小，所以用迭代器向前一位的区间和算一下试试。
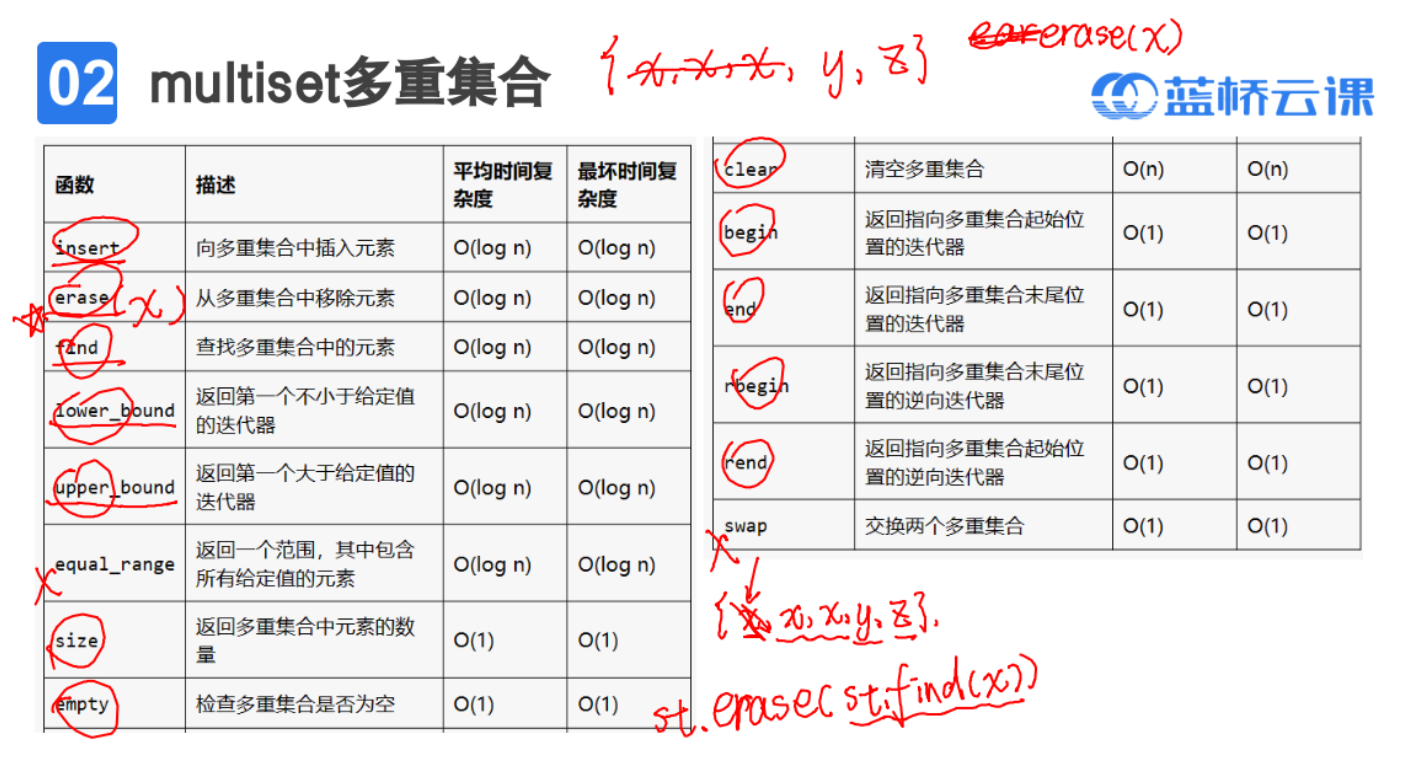
删除时如果用数字删会删全部，如果用迭代器删只删除指定位置
7.数字接龙
#include<bits/stdc++.h>
using namespace std;
const int N=20;
int a[N][N];//存放图
string path;//存路径
bool st[N][N];//存这个点是否经过
bool edge[N][N][N][N];//edge[i][j][x][y]表示起点(i,j)终点(x,y)的斜线是否经过 处理交叉问题
int n,k;
//方向向量
int dx[]={-1,-1,0,1,1,1,0,-1};//0-7 行
int dy[]={0,1,1,1,0,-1,-1,-1};//列
bool dfs(int x,int y){
if(x==n-1&&y==n-1){//搜到终点
return path.size()==n*n-1;//如果恰好经过n*n-1步到达终点，说明方案可行的
}
st[x][y]=true;//经过当前点
for(int i=0;i<8;i++) {
int bx=x+dx[i];
int by=y+dy[i];
if(bx>=n||bx<0||by>=n||by<0){
//越界
continue;
}
if(st[bx][by]){
continue;//经过了（防止重复走）
}
if(i%2&&(edge[bx][y][x][by]||edge[x][by][bx][y])){//只有斜线才防止交叉即1,3,5,7方向
continue;
}
if(a[bx][by]!=(a[x][y]+1)%k){//不满足走的要求
continue;
}
edge[x][y][bx][by]=true;//恢复
path+=i+'0';
if(dfs(bx,by)){//注意只要找到了就可退出！！
return true;
}
edge[x][y][bx][by]=false;
path.pop_back();
}
st[x][y]=false;//恢复现场
return false;//不存在路径-->有可能根本走不到终点！
}
int main(){
cin>>n>>k;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>a[i][j];
}
}
if(!dfs(0,0)){//从起点（0,0） 开始搜没有搜到
cout<<"-1" ;
}
else{
cout<<path;
}
return 0;
}
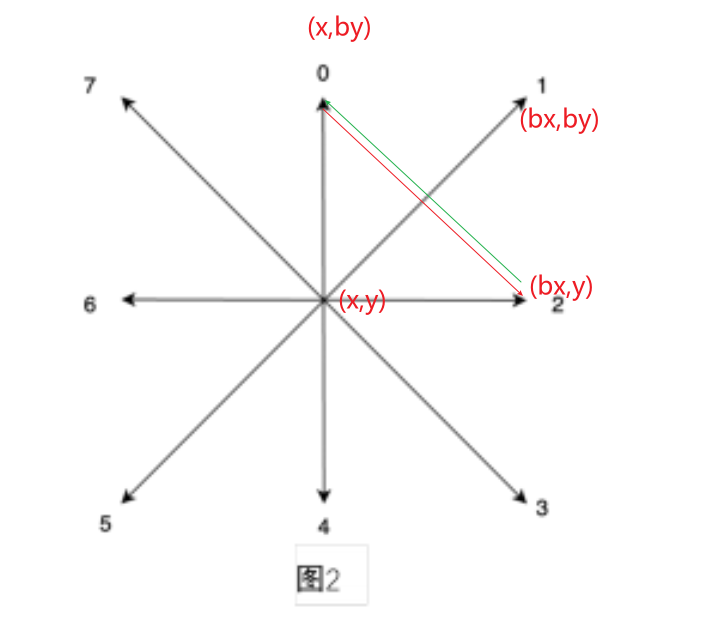
交叉：
双方向x,by->bx,y和bx,y->x,by如果存在 就交叉会和斜线方向
浙公网安备 33010602011771号