克鲁斯卡尔算法

克鲁斯卡尔算法

稀疏图-->用克鲁斯卡尔算法

克鲁斯卡尔算法套路：

首先存放每条边用struct

然后按照权值从小到大排序

然后如果这条边的两个端点已经在一个连通块就不要把这条边放进来（因为生成树不能有闭合回路）如已经有边12，边13不能再放入边23

判断连通块用find函数

利用并查集算法判断连通块

 

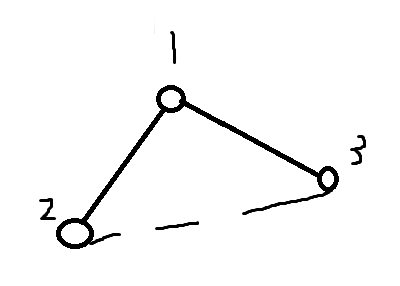
并查集：

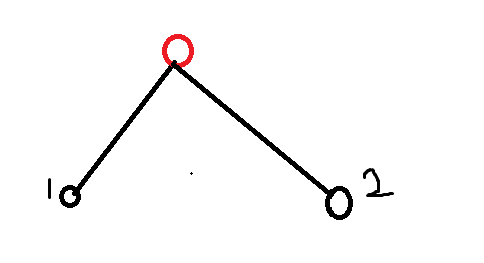
点1,2如果有共同祖先那么在同一个连通块find（x）=find(y)

find找祖宗函数

P[x]存放祖宗

P[x]=x就是P[x]存放的就是x下标那么p[x]就是祖宗就可以返回否则递归找父亲的父亲P[x]=find(P[x])

 

int find(int x){//并查集找祖宗

if(P[x]!=x){//不是祖宗 就找父亲的父亲

P[x] =find(P[x]);//递归

 

}

 

[//]: # (打卡模板，上面预览按钮可以展示预览效果 ^^)
考点：结构体，结构体比较，并查集找祖宗
```
//这里填你的代码^^
#include<bits/stdc++.h> 
using namespace std;
const int N=200006;
struct p{//存放边，端点是a，b
	int a;
	int b;
	int w;//权值
}e[N];
bool com(p x,p y){//结构体排序，比较函数
	return x.w<y.w;
}
int n,m;//n个顶点，m条边 
int P[N];//存放祖宗 
int find(int x){//并查集找祖宗
if(P[x]!=x){//不是祖宗 就找父亲的父亲
P[x] =find(P[x]);//递归

}
return 	P[x];
}
int main(){
	cin>>n>>m;
	int u,v,W;
for(int i=0;i<m;i++){
	cin>>u>>v>>W;
	e[i]={u,v,W};
}
sort(e,e+m,com);//从小到大排序边长
int cnt=0;//连通的边数
int res=0;//最小生成树权值和
//利用并查集判断连通块
for(int i=1;i<=n;i++) {
	P[i]=i;//祖先先定为点的下标  ** **** ** 
}
for(int i=0;i<m;i++){
	int x=e[i].a;
	int y=e[i].b;
	int z=e[i].w;
	if(find(x)!=find(y)){//祖宗不同
	P[find(x)] =find(y);
	res+=z;
	cnt++;
		
	}
 
}


if(cnt<n-1) cout<<"impossible";
else{
	cout<<res;
}
 

return 0;
}
//注意代码要放在两组三个点之间，才可以正确显示代码高亮哦~
```