线性代数

线性代数

一.标量

只有一个元素的张量

import torch#pytorch引用
x=torch.tensor(3.0)
y=torch.tensor(4.0)
print(x)
print(y)
print(x+y)
print(x**y)#x的y次方

二.向量 

（1）由标量值组成的列表

a=torch.arange(5)
print(a)
print(a[3])#下标从0开始

输出：

（2）张量长度和形状

h=torch.tensor([1,8,2])
print(len(h))#张量长度
print(h.shape)#张量形状，因为这个是一维向量所以结果是[张量长度]

输出：

（3）创建矩阵，reshape重新设定形状

A=torch.arange(16).reshape(2,8)#2行8列16个元素
print(A)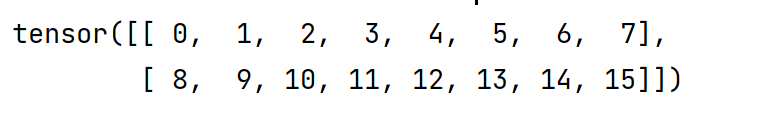

 

（4）转置

A=torch.arange(12).reshape(3,4)
print(A)
print("-------------------------")
print(A.T)#转置.T

(5)对称矩阵A^T=A

B=torch.tensor([[1,2,3],[2,0,4],[3,4,5]])
print("转置前：")
print(B)
print("---------------------------")
print("转置后")
print(B.T)
print(B.T==B)#对比每个元素是否相等，相等用True

 

（6）三维矩阵

C=torch.arange(24).reshape(2,3,4)#2个部分，每个部分3行4列。三维，从左到右1~3维
print(C)

tensor([[[ 0,  1,  2,  3],

         [ 4,  5,  6,  7],

         [ 8,  9, 10, 11]],

 

        [[12, 13, 14, 15],

         [16, 17, 18, 19],

         [20, 21, 22, 23]]])

(7)clone（）重新分配地址，将值复制过去！

D=torch.arange(24).reshape(4,6)
print("D矩阵：")
print(D)
print(id(D))
E=D.clone()
print("E矩阵：")
print(E)
print(id(E))
print(E+D)

(8）矩阵乘法（点乘）

D=torch.arange(24).reshape(4,6)
E=D.clone()
print(E*D)

D矩阵，E矩阵都是这样如下

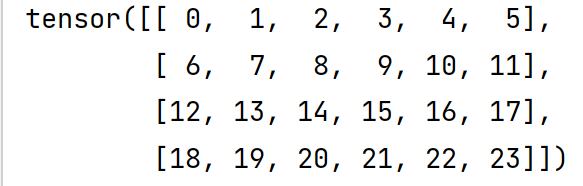
结果输出：

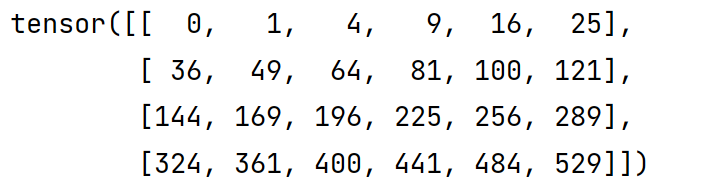
（9）降维

import torch
A=torch.arange(12).reshape(3,4)
print(A)
print(A.sum())#对所有元素求和
print(A.sum(axis=0))#0维指的是对每一列的所有行求和
print(A.sum(axis=1))#1维，对每一行的所有列求和
print(A.sum(axis=[0,1]))#0,1两个维度就是对所有元素求和

 

 

 （10）求平均值

import torch
A=torch.arange(12,dtype=torch.float32).reshape(3,4)#在arrange里要设置变量类型为float或复合型
print(A.sum())
print(A)
#print(A.size)
print(A.mean())
print(A.mean(axis=0))#第0维平均值

 

 （11）非降维

import torch
A=torch.arange(12,dtype=torch.float32).reshape(3,4)
print("A:")
print(A)
print("A.sum(axis=1)")#按列求和
print(A.sum(axis=1))
print(" A.sum(axis=1, keepdims=True)")#按列求和且保持维度不变
sum_A = A.sum(axis=1, keepdims=True)
print(sum_A)
print("A/sum_A")#A中每一个元素除以sum_A对应行的元素
print(A / sum_A)
print("A.cumsum(axis=0)")
print(A.cumsum(axis=0))#按行依次叠加！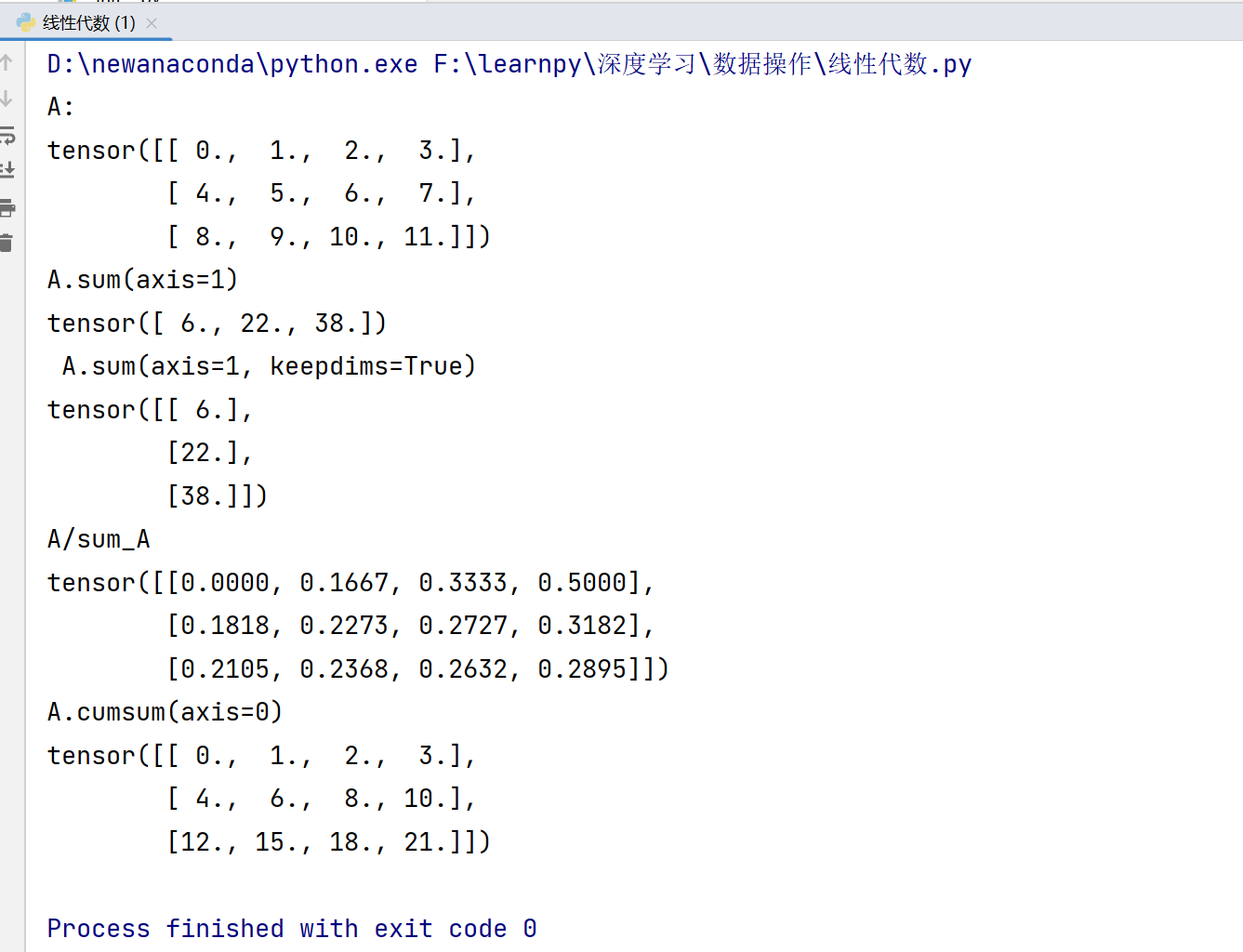

 

 （12）点积（正常向量积）

import  torch
import numpy as np
x=np.arange(4)
y=np.ones(4)
print(x)
print(y)
print(np.dot(x,y))
print(np.sum(x*y))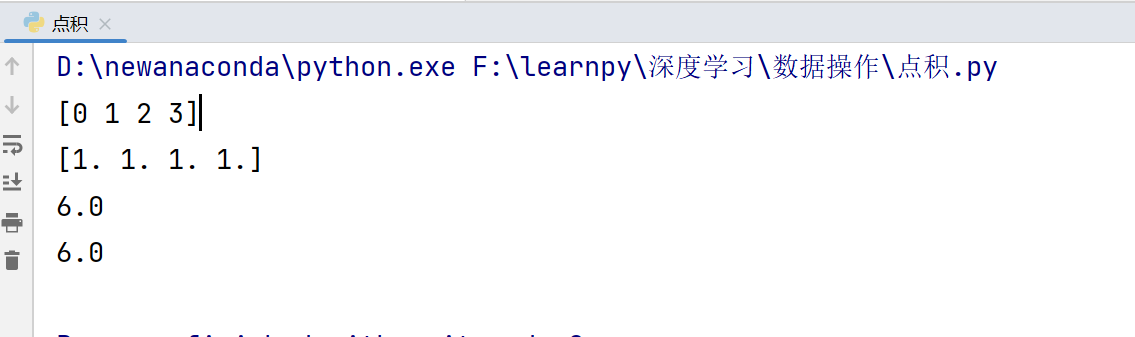

import numpy as np
A=np.arange(12).reshape(3,4)
print(A)
B=np.arange(8).reshape(4,2)
print(B)
print(np.dot(A,B))

(13)对应位置相乘

---

按特定轴求和详解

axis：轴

axis=0-->行

axis=1-->列

求和：

1.假如矩阵是5行4列

axis=0按行求和消除行维度

axis=1按列求和消除列维度

2.假如是三维矩阵shape(2,5,4)-->2部分，每部分5行4列

按axis=1求和-->消除中间那维度，变成(2,4)

按axis=0求和:消除最低维，变成（5,4）

按axis=2求和：消除最高维，变成（2,5）

keepdims=True保持维度不变

例如对一个三维矩阵（2,5,4）

按axis=0,1求和：

变为（1,1,4）