2017蓝桥杯省赛b组

2017蓝桥杯省赛b组

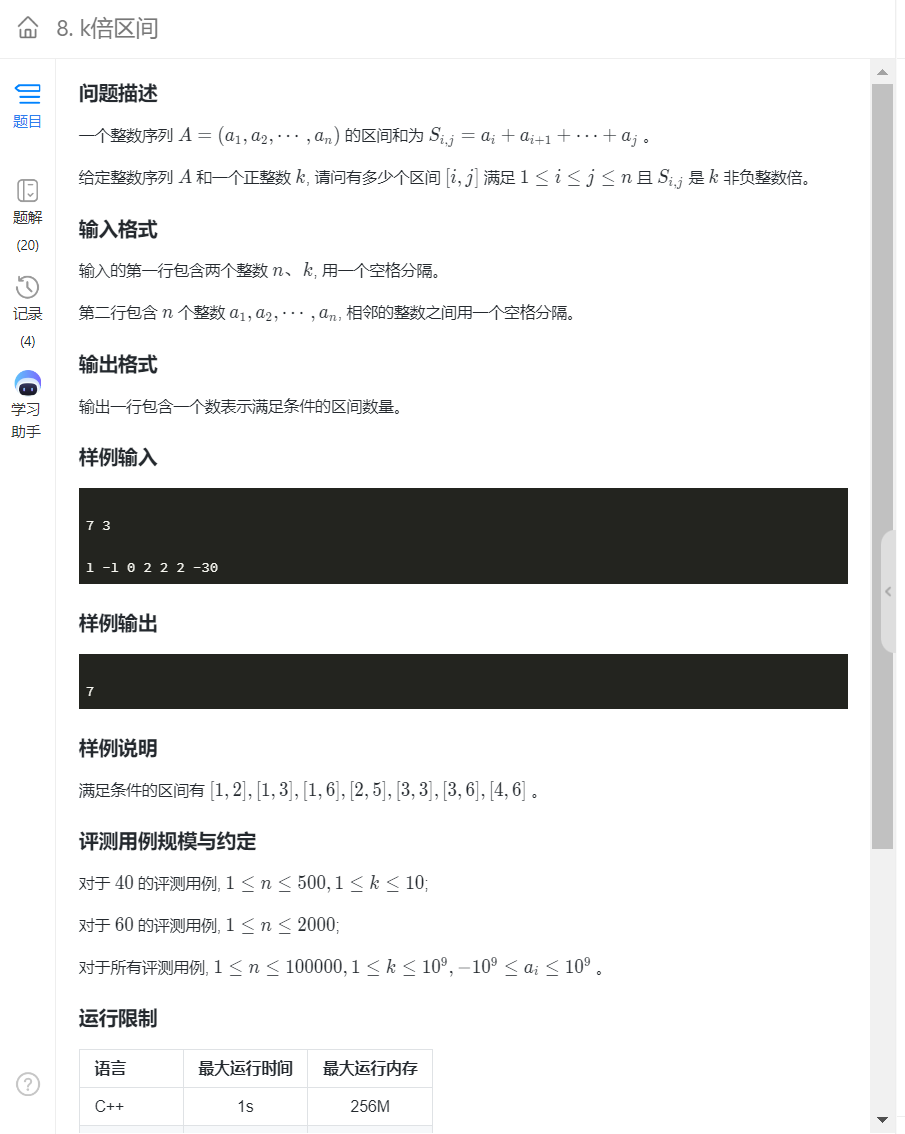
#include<bits/stdc++.h>

using namespace std;

//用一个map，存放余数，和同余数的前缀和

typedef long long int ll;

map<int,vector<ll>>p;

int main(){

int n,k;//n个数，

cin>>n>>k;

ll cnt=0;

ll sum=0;//前缀和

int a;

p[0].push_back(0);

for(int i=1;i<=n;i++){

cin>>a;

sum=sum+a;//前缀和

int b=(sum%k+k)%k;//余数

sort(p[b].begin(),p[b].end());

ll num=upper_bound(p[b].begin(),p[b].end(),sum)-p[b].begin();//找了多少个满足条件的

cnt+=num;

p[b].push_back(sum);

}

cout<<cnt;

return 0;

}

思路：计算任意区间和-->前缀和

如果只用前缀和然后配上双重循环会超时（过60%）

正解：

区间和是k的倍数：

加入s[ ]是前缀和数组

那么(s[r]-s[l-1])%k==0此时l∈[1,n]

为了好看写成(s[r]-s[l])%k==0此时l∈[0,n-1]

所以这道题转为当两个前缀和除以k同余那么这个区间是k的倍数

所以我们想到用一个map存放余数和当前余数对应的不同前缀和数组map<int,vector<int>>

注意ai可以小于0，所以可能余数小于0，所以为了化正应该写成（s[i]%k+k）%k

本题当前前缀和写成sum

本题枚举的是右边界所以要很早的是以当前右边界有多少左边界满足条件：

做法是先将map里以当前余数做第一维的数组里每一个元素进行从小到大排序（数组里放的是在他之前进来的元素都在他左边）

因为是非负倍数，所以只要比当前sum小于或等于的所有元素所以upper_bound二分找第一个比他大的元素-->计算出满足当前条件的元素个数

然后加在结果里

把这个余数，前缀和组合放进map里

最后输出cnt答案

 

 

完整代码

 #include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
int main(){
	map<int,vector<ll> >p;//存放余数和对应前缀和,注意前缀和可能超int所以用ll，然后对于c++的vector <>与外面>有个空格 
	int n,k;
	cin>>n>>k;
	ll sum=0;//前缀和
	int a;//输入当前数据 
	//初始余数为0，前缀和为0放入map 
	p[0].push_back(0);
	ll ans=0;//存放答案 
	for(int i=1;i<=n;i++) {
		cin>>a;
		sum=sum+a;//计算当前前缀和
		int b=(sum%k+k) %k;//计算当前余数
		 //对同余的已经进map的所有元素进行从小到大排序
		 sort(p[b].begin(),p[b].end()) ;
		 ans=ans+upper_bound(p[b].begin(),p[b].end(),sum) -p[b].begin();//在答案上加上以当前点作为右边界的 所有区间个数 
		 //把当前余数，前缀和放入map
		 p[b].push_back(sum);
	}
	cout<<ans;
	return 0;
}

包子凑数

 

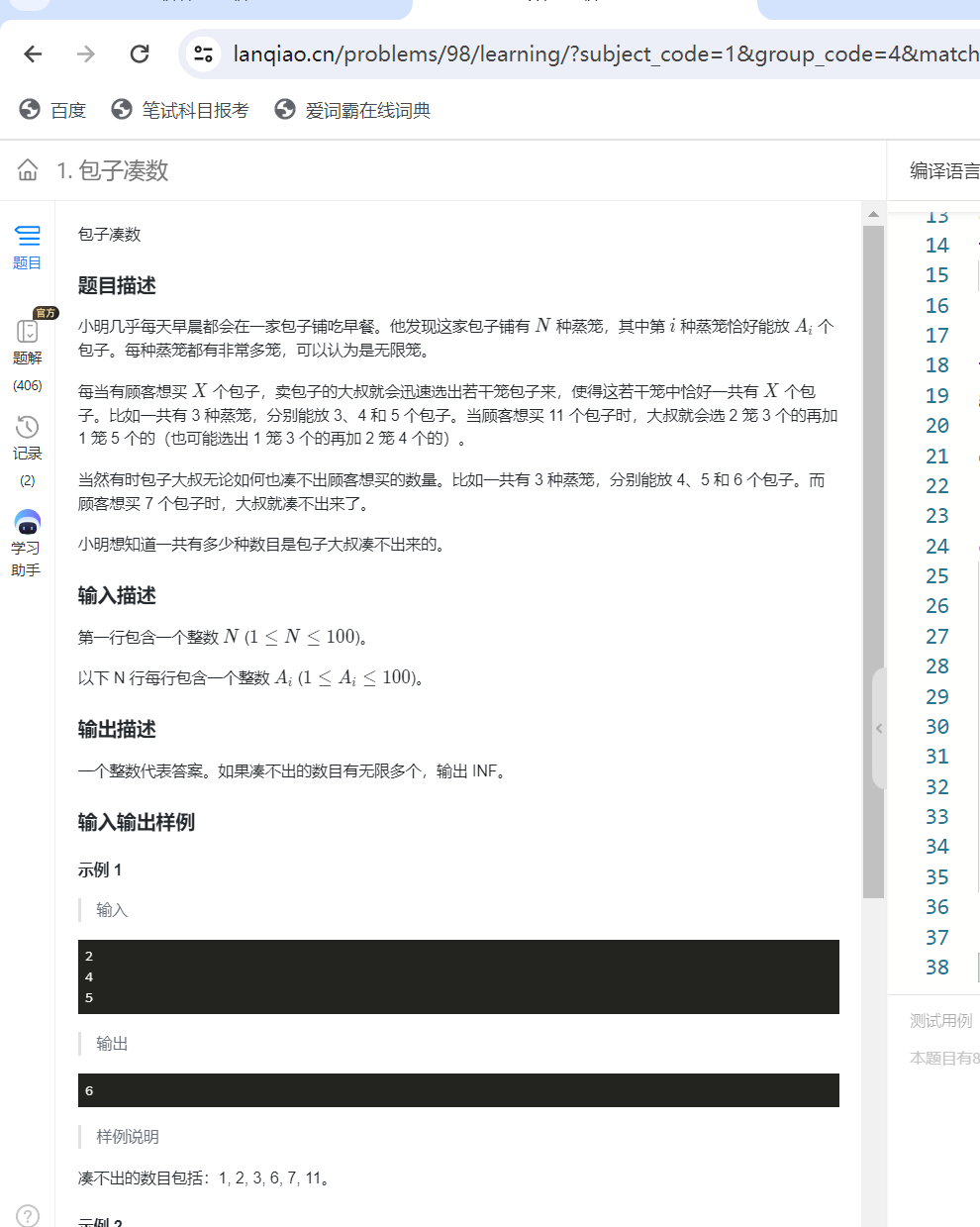
这个题需要稍微猜一下，凑不出的包子数最大10000左右如果不是无穷多种凑不出来

考点：

考察算法：

1.gcd最大公因数

有一个理论如果这堆数的最大公因数不等于1，说明他们都是一个数的倍数，那一定凑不出不为这个数倍数的数，所以有无穷多种包子数凑不出。

2.完全背包

完全背包（因为每种包子有很多笼），问的是不能凑出的数目，所以需要一个完全背包且为bool型dp

完整代码

 

#include<bits/stdc++.h> 

using namespace std;

const int N=10010;//最大凑不出的包子数

const int M=110;//包子类型

 int a[M];//包子类型数组

 bool dp[M][N];//dp[i][j]表示取到第i种包子凑出的包子数为j这种方案是否可行

 int n;//包子类型数（输入） 

 //最大公因数算法

 int gcd(int x,int y) {

  if(y==0)return x;

  else return gcd(y,x%y);

 }

int main(){

  cin>>n;

  int gy=0;//最大公因数 

  //背包问题最好下标从1开始类型下标 

  for(int i=1;i<=n;i++){

    cin>>a[i];

    gy=gcd(a[i],gy) ;

  }

  if(gy!=1)cout<<"INF";//有无穷多种凑不出，因为最大公因数不等于1

  else{//有限种凑不出包子数

  dp[0][0]=true;//取到第0种时包子数是0的方案是true 

  //完全背包(处理方案） 

   for(int i=1;i<=n;i++){//遍历到哪种类型包子 

    for(int j=0;j<N;j++) {//凑出的包子数 

      dp[i][j]=dp[i-1][j];//第i种不取,因为有i-1做下标所以一开始让i从1开始，即包子类型从1开始标号 

/*

用或是因为只要取或不取任意一种能凑出来这个包子数即可 

 dp[i][j]=dp[i-1][j]|dp[i-1][j-a[i]]|dp[i-1][j-2*a[i]]|dp[i-1][j-3*a[i]]...第i种取多少笼

为了减少循环可以 找规律如何凑出后面这一串 

 dp[i][j-a[i]]=dp[i-1][j-a[i]]|dp[i-1][j-2*a[i]]|dp[i-1][j-3*a[i]]...

-->得到 

dp[i][j]=dp[i-1][j]|dp[i][j-a[i]]

注意：下标需要大于等于0 这也就是说j-a[i]>=0才或上他 

*/

if(j-a[i]>=0){

  dp[i][j]|=dp[i][j-a[i]];

}

     }

   }

  //  计数凑不出包子数

  int ans=0;

   for(int i=0;i<N;i++){

    if(!dp[n][i])ans++;

   }

   cout<<ans;

  } 

}