2015年蓝桥杯六届省赛大学B组真题
2015年蓝桥杯六届省赛大学B组真题
1.奖券数目

2.星系炸弹

3.三羊献瑞
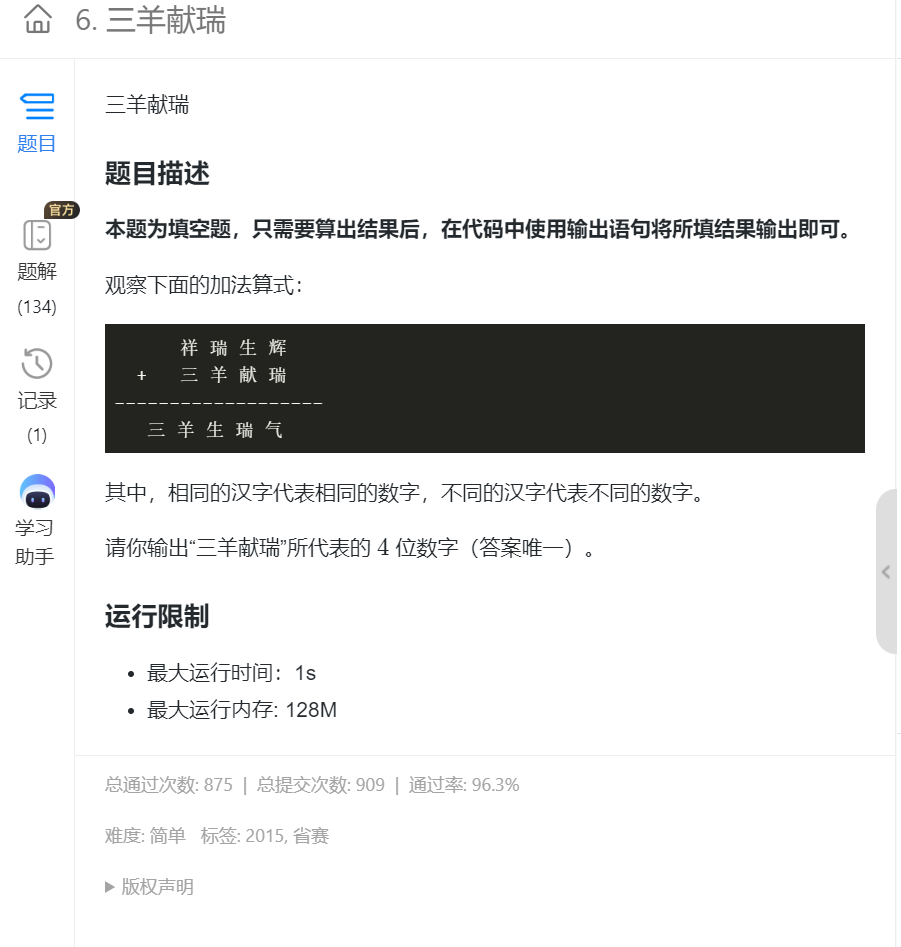
枚举
4.格子中输出
#include <stdio.h>
#include <string.h>
void StringInGrid(int width, int height, const char* s)
{
int i,k;
char buf[1000];
strcpy(buf, s);
if(strlen(s)>width-2) buf[width-2]=0;
printf("+");
for(i=0;i<width-2;i++) printf("-");
printf("+\n");
for(k=1; k<(height-1)/2;k++){
printf("|");
for(i=0;i<width-2;i++) printf(" ");
printf("|\n");
}
printf("|");
printf("%*s%s%*s",_____________________________________________); //填空
printf("|\n");
for(k=(height-1)/2+1; k<height-1; k++){
printf("|");
for(i=0;i<width-2;i++) printf(" ");
printf("|\n");
}
printf("+");
for(i=0;i<width-2;i++) printf("-");
printf("+\n");
}
int main()
{
StringInGrid(20,6,"abcd1234");
return 0;
}考点:
printf("%*s%s%*s",(width-strlen(buf)-2)/2," ",buf,(width-strlen(buf)-2)/2," "); //填空答案
"%*s",数字,字符串
表示从第几个位置开始输出字符串,第一个位置为1号位!


5.九数组分数
6.移动距离
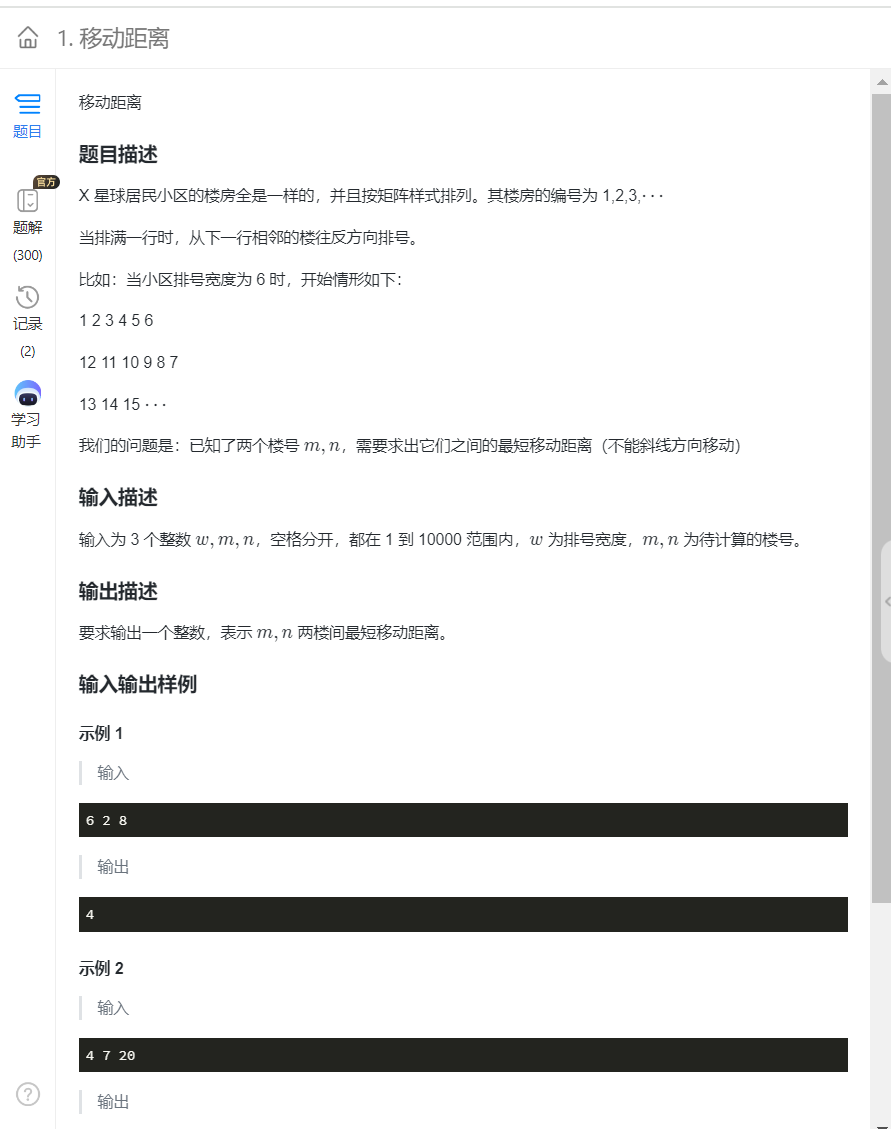
#include <bits/stdc++.h>
using namespace std;
int main()
{
int w,m,n;
cin>>w>>m>>n;
int h=0;
int z=0;
int x1,y1;
int x2,y2;
int sign=1;
for(int i=1;i<=10000;i++){
//考察走楼梯,语法
z=z+sign;
if(z>w){
z=w;
h++;
sign=-1;
}
if(z<1){
z=1;
sign=1;
h++;
}
if(i==m){
x1=h;
y1=z;
}
if(i==n){
x2=h;
y2=z;
}
}
//注意相减可能<0会抵消,所以abs绝对值
cout<<abs(x2-x1)+abs(y2-y1);
// 请在此输入您的代码
return 0;
}7.加法变乘法

计算思路:可以求出满足条件的乘号位置,方法是遍历这两个乘号可能的位置
8.牌型种数

思路:暴力,将13种牌型都枚举
十三种排序:A,2-10,J,Q,K
#include<bits/stdc++.h>
using namespace std;
int main(){
long long int cnt=0;
for(int a=0;a<=4;a++){//每张牌最多取4次(因为4色)
for(int b=0;b<=4;b++){
for(int c=0;c<=4;c++){
for(int d=0;d<=4;d++){
for(int e=0;e<=4;e++){
for(int f=0;f<=4;f++){
for(int g=0;g<=4;g++){
for(int h=0;h<=4;h++){
for(int i=0;i<=4;i++){
for(int j=0;j<=4;j++){
for(int k=0;k<=4;k++){
for(int l=0;l<=4;l++){
for(int m=0;m<=4;m++){
if(a+b+c+d+e+f+g+h+i+j+k+l+m==13){
cnt++;
}
}
}
}
}
}
}
}
}
}
}
}
}
}
cout<<cnt;
}
提交答案:
#include<bits/stdc++.h>
using namespace std;
int main(){
cout<<3598180;
return 0;
}
9.生命之树(最大权值子树和)
注意遍历相邻点时父亲结点不要再重新遍历。
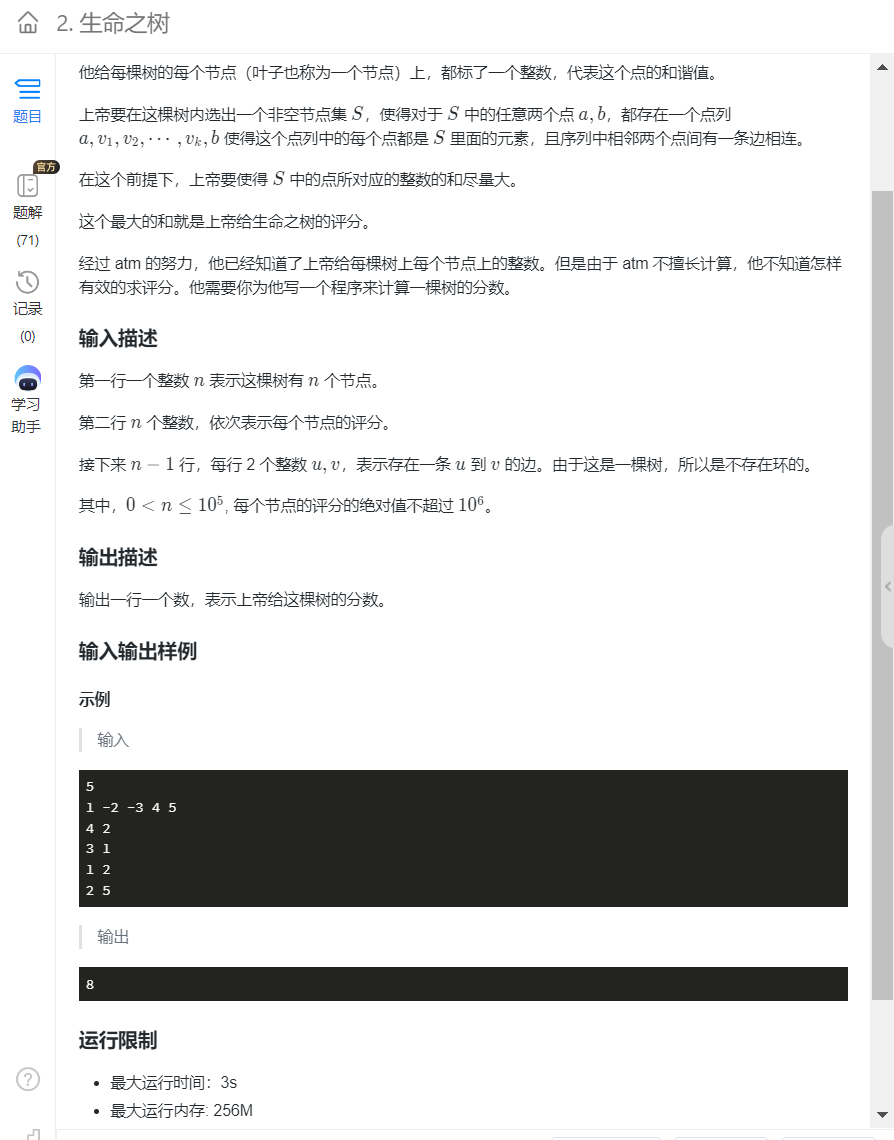
算法:树状dp+dfs+邻接表存图
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const int N=1e5+6;
const int M=2*N;
int e[N];//存放每个点的值
int idx;//当前已经存在几个点
int h[N] ;//存放头结点
int ne[M] ;//存放当前结点指向的下一节点
int w[N];//每个点的分(权值)
int n;
ll f[N];//f[i]表示以i为根节点的连通块权值和的最大值(dp)
void add(int a,int b){//邻接表存图
//建立a->b这条边,思想是将b结点放入a的邻接单链表里
//1.存插入值
e[idx]=b;
//2.连接
ne[idx] =h[a];
h[a]=idx++;
}
//dfs计算树形dp其实是递归
void dfs(int a,int father) {
f[a]=w[a];
for(int i=h[a];i!=-1;i=ne[i]){
int j=e[i];
if(j!=father){
//
dfs(j,a);
f[a]+=max(0ll,f[j]);
}
}
}
int main(){
memset(h,-1,sizeof(h)) ;
cin>>n;
for(int i=1;i<=n;i++){
//点从1号开始标
cin>>w[i] ;
}
//邻接表存图,邻接表就是多个单链表,每个单链表存放与当前点相邻的点
for(int i=0;i<n-1;i++){//对于树,n个结点对应n-1条无向边
int a,b;
cin>>a>>b;
//无向边就要双向存
add(a,b);
add(b,a);
}
dfs(1,-1) ;//dfs计算每个结点为根节点的最大权值子树包括这个根的权值
ll res=0;
for(int i=1;i<=n;i++){
res=max(res,f[i]);//遍历看哪个为根节点的连通块权值和最大
}
cout<<res;
return 0;
}
完整代码
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const int N=1e5+6;//结点数
const int M=2*N;
int w[N] ;//每个结点的评分
int h[N] ;//头结点
//因为树是无向图,所以一条边存两遍(a,b)(b,a),所以e[ ],ne[ ]容量开两遍因为存节点下标
int e[M] ;//存放当前点的下标
int ne[M];//next指针,指向下一个节点
int idx;//当前在第几个点
ll dp[N];//dp[u]表示以u为根的连通块最大权值和,树形dp
int n;//顶点个数
void add(int a,int b) {
//添加a->b这条边
//利用头插法,在a头结点后面插入b
e[idx]=b;//第一步存放b点
//第二步:连接
ne[idx] =h[a];
h[a]=idx++;
}
//树状dp,用递归dfs
void dfs(int u,int father){
dp[u]=w[u];//以u为根的连通块,他包含u这个点作为根
for(int i=h[u];i!=-1;i=ne[i]){//遍历u的所有邻结点
int j=e[i];
if(j!=father){//防止重复遍历,所以遍历邻结点但不能是他的父节点
dfs(j,u);//递归,下一层
dp[u]+=max(0ll,dp[j]);//dp[u]以u为根节点最大连通块权值和,所以只加上非负的邻接点
}
}
}
int main(){
memset(h,-1,sizeof(h));//初始化头结点链表
cin>>n;
for(int i=1;i<=n;i++){
cin>>w[i];;//每个结点的权值(评分),注意从1号结点开标
}
//邻接表建图,邻接表就是多个单链表,每个单链表是存放与当前结点相连的点
for(int i=0;i<n-1;i++){
//有n个顶点的树拥有n-1条无向边
int a,b;
cin>>a>>b;
//建立边存入邻接表
add(a,b);
add(b,a);
}
//dfs
dfs(1,-1);//从第一个结点开始搜,然后他的父节点是-1
ll ans=0;
for(int i=1;i<=n;i++){
ans=max(ans,dp[i]);
}
cout<<ans;
return 0;
}核心代码
邻接表存图
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const int N=1e5+6;//结点数
const int M=2*N;
int w[N] ;//每个结点的评分
int h[N] ;//头结点
//因为树是无向图,所以一条边存两遍(a,b)(b,a),所以e[ ],ne[ ]容量开两遍因为存节点下标
int e[M] ;//存放当前点的下标
int ne[M];//next指针,指向下一个节点
int idx;//当前在第几个点
ll dp[N];//dp[u]表示以u为根的连通块最大权值和,树形dp
int n;//顶点个数
void add(int a,int b) {
//添加a->b这条边
//利用头插法,在a头结点后面插入b
e[idx]=b;//第一步存放b点
//第二步:连接
ne[idx] =h[a];
h[a]=idx++;
}
int main(){
memset(h,-1,sizeof(h));//初始化头结点链表
//邻接表建图,邻接表就是多个单链表,每个单链表是存放与当前结点相连的点
for(int i=0;i<n-1;i++){
//有n个顶点的树拥有n-1条无向边
int a,b;
cin>>a>>b;
//建立边存入邻接表
add(a,b);
add(b,a);
}
}树状dp+dfs
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const int N=1e5+6;//结点数
const int M=2*N;
int w[N] ;//每个结点的评分
int h[N] ;//头结点
//因为树是无向图,所以一条边存两遍(a,b)(b,a),所以e[ ],ne[ ]容量开两遍因为存节点下标
int e[M] ;//存放当前点的下标
int ne[M];//next指针,指向下一个节点
int idx;//当前在第几个点
ll dp[N];//dp[u]表示以u为根的连通块最大权值和,树形dp
int n;//顶点个数
//树状dp,用递归dfs
void dfs(int u,int father){
dp[u]=w[u];//以u为根的连通块,他包含u这个点作为根
for(int i=h[u];i!=-1;i=ne[i]){//遍历u的所有邻结点
int j=e[i];
if(j!=father){//防止重复遍历,所以遍历邻结点但不能是他的父节点
dfs(j,u);//递归,下一层
dp[u]+=max(0ll,dp[j]);//dp[u]以u为根节点最大连通块权值和,所以只加上非负的邻接点
}
}
}
int main(){
//dfs
dfs(1,-1);//从第一个结点开始搜,然后他的父节点是-1
ll ans=0;
for(int i=1;i<=n;i++){
ans=max(ans,dp[i]);
}
cout<<ans;
return 0;
}10.垒骰子
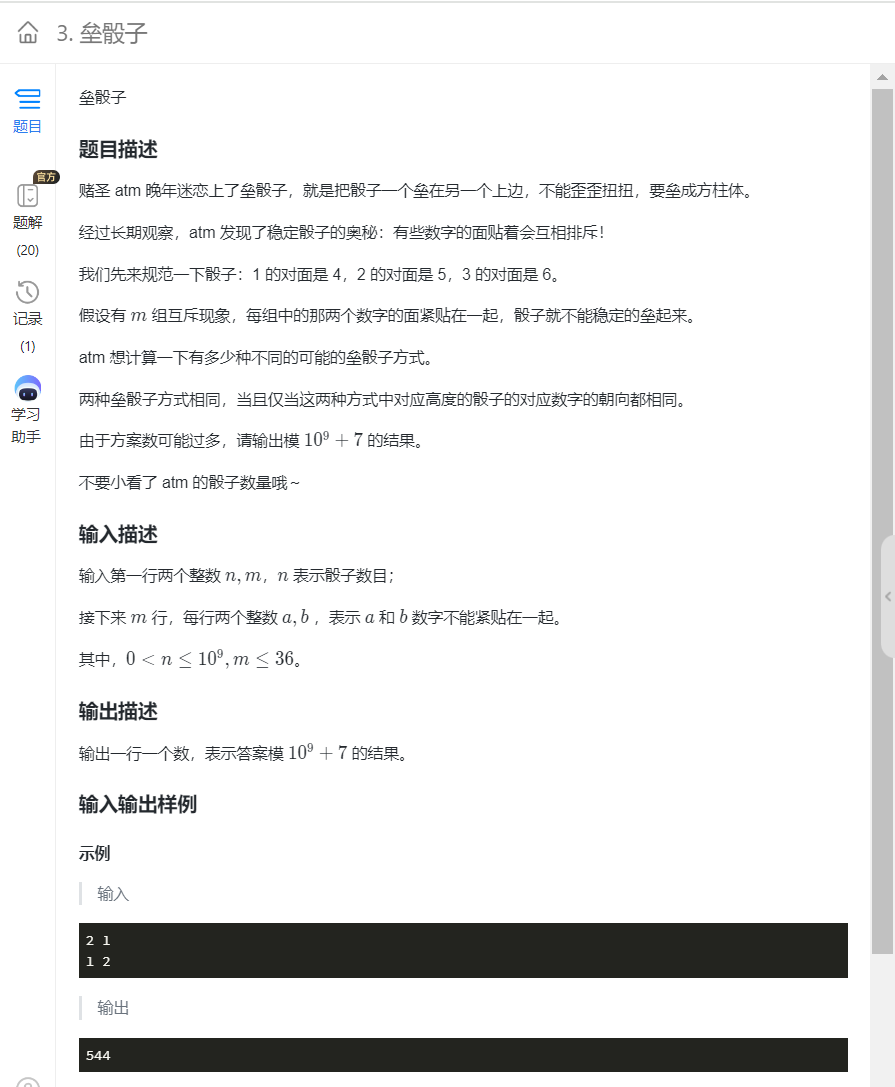
分析代码
点数0~5
#include<bits/stdc++.h>
using namespace std;
const int N=6;
typedef long long int ll;
const int mod=1e9+7;
int a[N][N];//带限制的矩阵,即系数矩阵
int ops(int x){
if(x>=3)return x-3;
return x+3;
}
//矩阵乘法
void mul(int c[N][N],int d[N][N],int e[N][N]){//d*e=c
static int t[N][N];
memset(t,0,sizeof (t));
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
for(int k=0;k<N;k++){
t[i][j]=(t[i][j]+(ll)d[i][k]*e[k][j])%mod;
}
}
}
memcpy(c,t,sizeof(t));
}
int main(){
int n,m;//n个骰子,m种限制
cin>>n>>m;
//系数矩阵初始化4,就是没限制
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
a[i][j]=4;
}
}
while(m--){//限制
int x,y;
cin>>x>>y;
x--;y--;//化为0~5点数
//这是下面那个骰子的系数矩阵,如果下面那个骰子上面是x不能转移到上面那个骰子的下面是y的情况也就是上面那个骰子上面是ops(y)
a[x][ops(y)]=0;
a[y][ops(x)]=0;
}
int f[N][N]={4,4,4,4,4,4};//存结果,初始是只有一个骰子那么每个点数做最上面的情况都是4
long long int ans=0;
for(int k=n-1;k;k>>=1){//快速幂,目的计算f*a的n-1次方
if(k&1) mul(f,f,a);//计算a*f,结果乘
mul(a,a,a);//基数变化
}
//最上面行就是答案,即用完所有骰子最上面骰子的上面是各个点数的情况数然后求和
for(int i=0;i<N;i++){
ans=(ans+f[0][i])%mod;
}
cout<<ans;
return 0;
}
if(k&1)乘法
乘方
}
int t[N][N];//暂存数组
memset(t,0,sizeof (t));
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
for(int k=0;k<N;k++){
t[i][j]=(t[i][j]+(ll)d[i][k]*e[k][j])%mod;
}
}
}
memcpy(c,t,sizeof(t));//将t数组内容放入c
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号