2016蓝桥杯省赛B组
2016蓝桥杯省赛B组
1.煤球数目
#include<bits/stdc++.h>
using namespace std;
int dp[200];
int main(){
int sum=0;
for(int i=1;i<=100;i++){
dp[i]=dp[i-1]+i;
sum+=dp[i];
}
cout<<sum;
return 0;
}
另一种写法
#include <iostream>
using namespace std;
typedef long long int ll;
ll ans;
ll a;
int main()
{
for(int i=1;i<=100;i++){
a=a+i;
ans+=a;
}
cout<<ans;
return 0;
}思路：
每一层煤球个数
0+1->1+2->3+3->6+4
答案：171700
2.生日蜡烛
（枚举）
某君从某年开始每年都举办一次生日p a r t y ，并且每次都要吹熄与年龄相同根数的蜡烛。
现在算起来，他一共吹熄了236根蜡烛。
请问，他从多少岁开始过生日p a r t y的？
请填写他开始过生日p a r t y 的年龄数。 注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。
思路1：就是age是开始过生日的年龄，然后看从此年龄开始过生日能否达到236或超过236，所以当内循环退出的时候就会检验如果因为等于236退出说明是答案，如果是超过236说明就是从这个年龄开始过生日凑不出来236
#include<bits/stdc++.h>
using namespace std;
int age;
int main(){
for(age=0;age<=236;age++){
int sum=0;
for(int i=age;sum<236;i++){
sum+=i;
}
if(sum==236){
cout<<age;
return 0;
}
}
return 0;
}
using namespace std;
int age;
int main(){
for(age=0;age<=236;age++){
int sum=0;
for(int i=age;sum<236;i++){
sum+=i;
}
if(sum==236){
cout<<age;
return 0;
}
}
return 0;
}
思路2：
就是236-->不可能过到236岁以后，所以内循环变量表示过到多少岁，终点是236，这样可以把以age为起点的所有情况变量，只要有sum=236就退出循环，输出答案。
答案：26
3.凑算式
陷阱：每一位从1开始，因为要确切计算所以用double防止整除陷阱，即便是用最小公倍数也会有整除陷阱所以用double。
我的解法
![]()
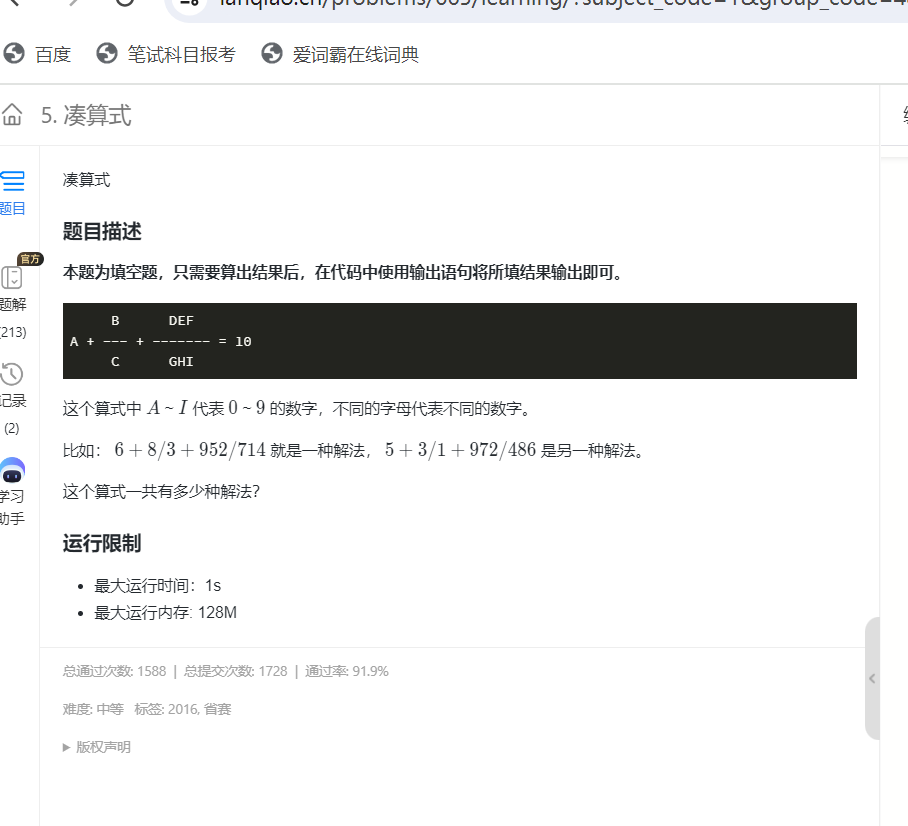
#include<bits/stdc++.h>
using namespace std;
int main(){
long long int ans=0;
for(double a=1;a<10;a++){
for(double b=1;b<10;b++){
if(b==a)continue;
for(double c=1;c<10;c++){
if(c==a||c==b)continue;
for(double d=1;d<10;d++){
if(d==a||d==b||d==c)continue;
for(double e=1;e<10;e++){
if(e==a||e==b||e==c||e==d)continue;
for(double f=1;f<10;f++){
if(f==a||f==b||f==c||f==d||f==e)continue;
for(double g=1;g<10;g++){
if(g==a||g==b||g==c||g==d||g==e||g==f)continue;
for(double h=1;h<10;h++){
if(h==a||h==b||h==c||h==d||h==e||h==f||h==g)continue;
for(double i=1;i<10;i++){
if(i==a||i==b||i==c||i==d||i==e||i==f||i==g||i==h)continue;
double p=d*100+e*10+f;
double q=g*100+h*10+i;
if(a+b/c+p/q==10){
ans++;
}
}
}
}
}
}
}
}
}
}
cout<<ans;
}标准答案：用dfs枚举每一位，因为要求每一位的值所以用搜索dfs。全排列
#include<bits/stdc++.h>
using namespace std;
double a[10];
int ans;
bool visit[10];
void dfs(int index){
if(index==9){//9位填满
if(a[0]+a[1]/a[2]+(a[3]*100+a[4]*10+a[5])/(a[6]*100+a[7]*10+a[8])==10){//对应A~I每一位
ans++;
return ;
}
}
//dfs
for(int i=1;i<10;i++){//为当前位赋值有1~9这几种可能值
if(!visit[i]){//如果这个值没有访问过就赋给当前位
visit[i]=true;//这个值被访问
a[index]=i;
dfs(index+1);//跳去下一层
visit[i]=false;//恢复现场
}
}
}
int main(){
dfs(0);
cout<<ans;
}4.交换瓶子
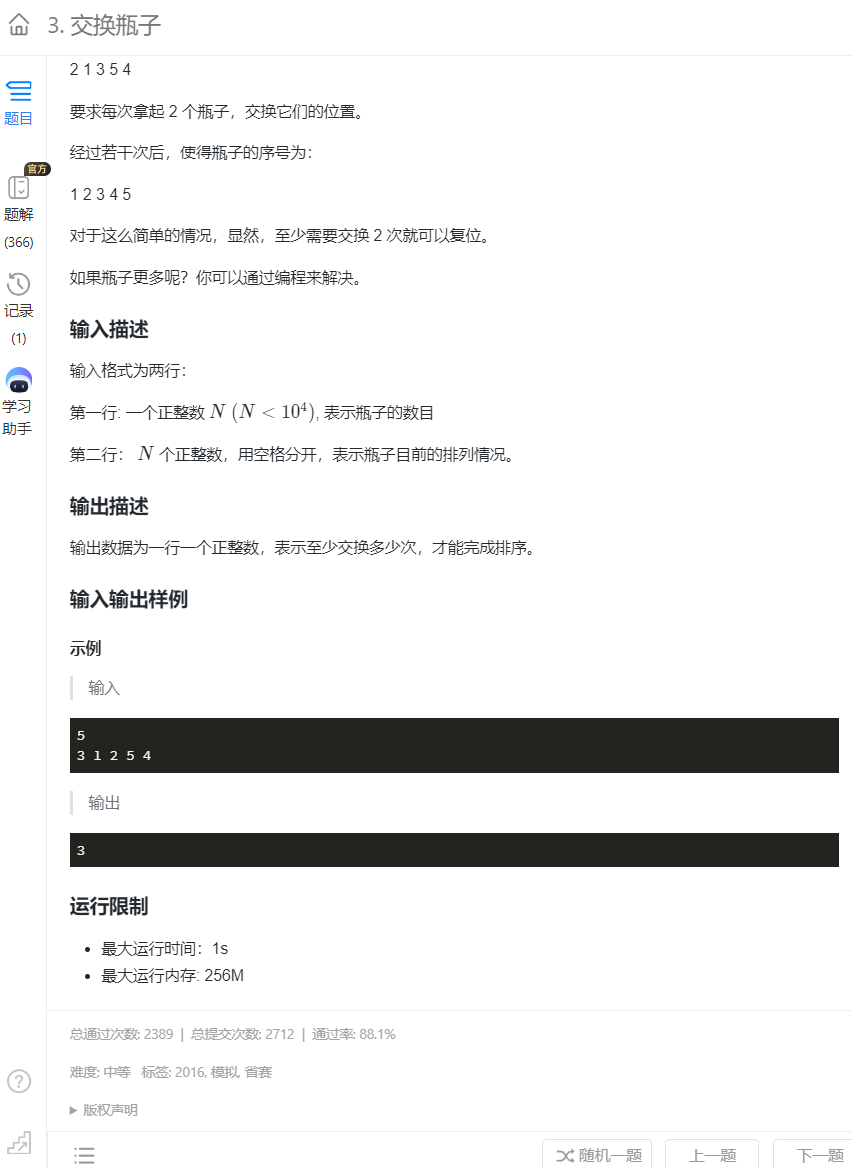
#include <iostream>
using namespace std;
const int N=1e4+6;
int a[N];
int n;
int ans;
int main()
{
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
if(a[i]!=i){
int z=a[i];
int temp=a[i];
a[i]=a[z];
a[z]=temp;
ans++;
i--;//注意一定要保证当前位置直到换到对才停
}
}
cout<<ans;
// 请在此输入您的代码
return 0;
}
贪心：
从左往右遍历所有瓶子，只要位置不对，就交换他和他应该在的位置上的瓶子，让这个瓶子归位。
5.四平方和
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin>>n;
for(int a=0;a<=sqrt(n/4);a++){
for(int b=a;b<=sqrt(n/4);b++){
for(int c=b;c<=sqrt(n/4);c++){
int d=sqrt(n-a*a-b*b-c*c);
if(a*a+b*b+c*c+d*d==n){
cout<<a<<" "<<b<<" "<<c<<" "<<d;
return 0;
}
}
}
}
return 0;
}
6.快速排序（填空题）
#include <stdio.h>
void swap(int a[], int i, int j)
{
int t = a[i];
a[i] = a[j];
a[j] = t;
}
int partition(int a[], int p, int r)
{
int i = p;
int j = r + 1;
int x = a[p];
while(1){
while(i<r && a[++i]<x);
while(a[--j]>x);
if(i>=j) break;
swap(a,i,j);
}
______________________;//填空
return j;
}
void quicksort(int a[], int p, int r)
{
if(p<r){
int q = partition(a,p,r);
quicksort(a,p,q-1);
quicksort(a,q+1,r);
}
}
int main()
{
int i;
int a[] = {5,13,6,24,2,8,19,27,6,12,1,17};
int N = 12;
quicksort(a, 0, N-1);
for(i=0; i<N; i++) printf("%d ", a[i]);
printf("\n");
return 0;
}
第七题：抽签（填空题）
#include <stdio.h>
#define N 6
#define M 5
#define BUF 1024
void f(int a[], int k, int m, char b[])
{
int i,j;
if(k==N){
b[M] = 0;
if(m==0) printf("%s\n",b);
return;
}
for(i=0; i<=a[k]; i++){
for(j=0; j<i; j++) b[M-m+j] = k+'A';
______________________; //填空位置
}
}
int main()
{
int a[N] = {4,2,2,1,1,3};
char b[BUF];
f(a,0,M,b);
return 0;
}
分析和答案
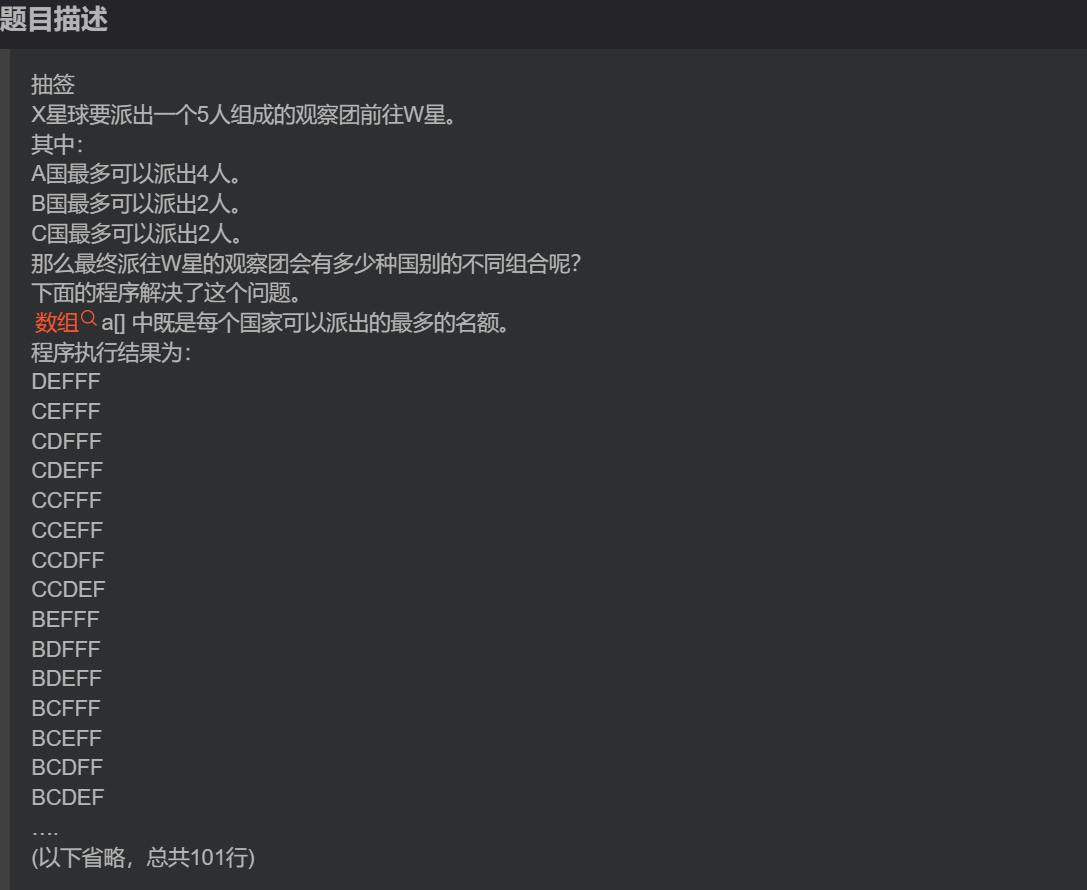
#include <stdio.h>
#define N 6
#define M 5
#define BUF 1024
void f(int a[], int k, int m, char b[])
{
int i,j;
if(k==N){
b[M] = 0;
if(m==0) printf("%s\n",b);
return;
}
for(i=0; i<=a[k]; i++){//当前这个国家分几个人
for(j=0; j<i; j++) b[M-m+j] = k+'A';//录入当前国家人
f(a,k+1,m-i,b);//答案，k+1表示换下一个国家，m-i表示上一次结束还需要分m人但是这次分了i人所以还要分m-i人，注意M，因为每次结束还需要分的人数不同不能用M。
}
}
int main()
{
int a[N] = {4,2,2,1,1,3};//存放每个国家人数
char b[BUF];//存放当前方案
f(a,0,M,b);
return 0;
}第八题：方格填数
注意：是这10个格子填的数不能一样，而且填的范围0~9
#include<bits/stdc++.h> using namespace std; int a[10]; int res; bool st[10]; bool check(){ if(abs(a[0]-a[1])==1||abs(a[0]-a[5])==1||abs(a[0]-a[4])==1||abs(a[0]-a[3])==1|| abs(a[1]-a[2])==1||abs(a[1]-a[6])==1||abs(a[1]-a[5])==1||abs(a[1]-a[4])==1|| abs(a[2]-a[5])==1||abs(a[2]-a[6])==1||abs(a[3]-a[4])==1||abs(a[3]-a[8])==1|| abs(a[3]-a[7])==1||abs(a[4]-a[5])==1||abs(a[4]-a[8])==1||abs(a[4]-a[7])==1|| abs(a[4]-a[9])==1||abs(a[5]-a[6])==1||abs(a[5]-a[8])==1||abs(a[5]-a[9])==1|| abs(a[7]-a[8])==1||abs(a[8]-a[9])==1||abs(a[6]-a[9])==1)return false; return true; } void dfs(int m){ if(m==10){ if(check()){ res++; } } for(int i=0;i<10;i++){ if(!st[i]){ st[i]=true; a[m]=i; dfs(m+1); st[i]=false; } } } int main(){ dfs(0);//从第0个位置开始搜 cout<<res; }
第9题：最大比例
10的9次方要开long longm
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 110;
int n;
LL a[N], b[N], x[N];//a是分子b是分母x是答案
LL gcd(LL a, LL b)
{
return b ? gcd(b, a % b) : a;
}
//辗转相减法LL gcd_sub(LL a, LL b)
{
if (a < b) swap(a, b);//辗转相减法一定要a大
if (b == 1) return a;
return gcd_sub(b, a / b);//注意虽然是辗转相减法但是指数相减对应的是相除
}
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> x[i];
sort(x, x + n);//排序
int cnt = 0;
for (int i = 1; i < n; i ++ )
if (x[i] != x[i - 1])//去重·
{
//每一项都除以第一项，并且化最简(除以最大的公因数）
LL d = gcd(x[i], x[0]);
a[cnt] = x[i] / d;
b[cnt] = x[0] / d;
cnt ++ ;
}
LL up = a[0], down = b[0];//结果的分子分母
for (int i = 1; i < cnt; i ++ )
{
//每一次和之前所求算最大公约数（辗转相减法）
为什么不用gcd因为指数相减更简单。并且这个数太大指数幂用gcd算不了。
up = gcd_sub(up, a[i]);
down = gcd_sub(down, b[i]);
}
cout << up << '/' << down << endl;
return 0;
}
满分代码
#include<bits/stdc++.h>
using namespace std;typedef long long int ll;
const int N=106;
ll x[N];//存放输入数
ll a[N];//存放分子
ll b[N];//存放分母
ll gcd(ll m,ll n){//这个更万能，用于求两个数的最大公因数
if(n==0)return m;
return gcd(n,m%n);
}
ll sub_gcd(ll m,ll n){//仅适用等比，这个时候才可以除求最大公因数，而且效率更高
if(m<n) swap(m,n);//重要
if(n==1)return m;
return sub_gcd(n,m/n);
}
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++){
cin>>x[i];
}
sort(x,x+n);//排序
int cnt=0;
//除以第0项
for(int i=1;i<n;i++){
if(x[i]!=x[i-1]){//去重
ll d=gcd(x[i],x[0]);
a[cnt]=x[i]/d;
b[cnt]=x[0]/d;
cnt++;
}
}
ll up=a[0];//结果分子
ll down =b[0];//结果分母
for(int i=1;i<cnt;i++){
up=sub_gcd(up,a[i]);
down=sub_gcd(down,b[i]);
}
cout<<up<<"/"<<down;
return 0;
} #include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const int N=110;
ll a[N];
ll gcd(ll x,ll y){
if(y){
return gcd(y,x%y);
}
else{
return x;
}
}
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
}
sort(a,a+n);
ll g=gcd(a[0],a[1]);
ll A=a[1]/g;
ll B=a[0]/g;
double d=(1.0*a[1])/a[0];
for(int i=2;i<n;i++){
if((1.0*a[i])/a[i-1]<d){
d=(1.0*a[i])/a[i-1];
g=gcd(a[i],a[i-1]);
A=a[i]/g;
B=a[i-1]/g;
}
}
cout<<A<<"/"<<B;
return 0;
}
/*
代码错误的原因把相邻数壁纸最小的当做公比
其实可能这两个数之间还有别的等级他们两个并不是相邻等级
*/补充：更相减损法
def gcd_by_subtraction(a, b):
while a != b:
if a > b:
a = a - b
else:
b = b - a
return a
num1 = 24
num2 = 36
result = gcd_by_subtraction(num1, num2)
print(f"{num1} 和 {num2} 的最大公因数是: {result}")
第十题：剪邮票
#include<bits/stdc++.h>
using namespace std;
int ans;
void dfs(int g[3][4],int i,int j){
//对当前点所在连通块dfs，类似于洪水漫灌，4个方向，上下左右。并且要访问当前点，访问过为防止重复遍历就变为0
g[i][j]=0;
if(i-1>=0&&g[i-1][j]==1)dfs(g,i-1,j);//上
if(i+1<=2&&g[i+1][j]==1)dfs(g,i+1,j);//下
if(j-1>=0&&g[i][j-1]==1)dfs(g,i,j-1);//左
if(j+1<=3&&g[i][j+1]==1)dfs(g,i,j+1);//右
}
//其实就是连通性检测，因为邮票减下来的要相连所以只有一个连通块（带1的连通块有一个）
bool check(int a[12]){
int g[3][4];//存整个图3行4列，要剪下来的用1目的是二维化
//开始用一维目的是将问题转化为数字的全排列
for(int i=0;i<3;i++){
for(int j=0;j<4;j++){
if(a[i*4+j]==1)g[i][j]=1;//一行4列，所以i*4+j
else g[i][j]=0;
}
}
int cnt=0;
for(int i=0;i<3;i++){
for(int j=0;j<4;j++){
if(g[i][j]==1){//是1才dfs遍历他所在的连通块
dfs(g,i,j);
cnt++;
}
}
}
return cnt==1;//连通块是1才true，因为这5张邮票要剪下来的一定是相连的。cnt表示连通块个数，如果剪得不合法那么cnt>1
}
int main(){
int per[]={0,0,0,0,0,0,0,1,1,1,1,1};//将二维格子抽象成一维数组（类比方格填数），1表示要剪下来的邮票（5张）。（7+5）
//靠的就是7个0和5个1的排序（全排列）
do{
if(check(per))ans++;//全排列枚举所有情况，check检查满足条件的有
}while(next_permutation(per,per+12));有重复元素的排列用next_permutation更好因为可以去重（本题多个0，多个1重复元素）
cout<<ans;
return 0;
}
注意：
next_permutation用法：这个函数能实现全排列
要先排序在全排列
法二：就是先把所有选法都选出来在12个格子里不重复选5个格子，因为担心选重复所以每次要取比上一次选的格子大的格子，当选完5个格子就做连通性的判断dfs2就是把前后左右相邻可走的所选中的邮票都走一遍！
#include<bits/stdc++.h>
using namespace std;
int path[5];
bool st[20];
int ans;
bool g[3][4];
int dx[]={-1,1,0,0};//行，上下左右
int dy[] ={0,0,-1,1};//列，上下左右
bool v[20];
void dfs2(int a,int b){
v[(a*4)+b+1]=false;
for(int i=0;i<4;i++){
int nx=a+dx[i];
int ny=b+dy[i];
if(nx<0||nx>2||ny<0||ny>3)continue;
if(v[nx*4+ny+1]==true){
dfs2(nx,ny);
}
}
}
bool check(){
memset(v,false,sizeof(v));
for(int i=0;i<5;i++){
v[path[i]]=true;//选中的 yp
}
int ltk=0;
for(int i=0;i<5;i++) {
int num=path[i];
if(v[num]==true){
dfs2((num-1)/4,(num-1)%4);
ltk++;
}
}
// cout<<ltk<<endl;
if(ltk==1)return true;
return false;
}
void dfs(int dep,int f){
if(dep==5){
if(check()){
ans++;
}
}
for(int i=f+1;i<=12;i++){
if(!st[i]){
st[i]=true;
path[dep]=i;
dfs(dep+1,i);
st[i]=false;
}
}
}
int main(){
dfs(0,0);
cout<<ans;
return 0;
}
浙公网安备 33010602011771号