2017省赛蓝桥杯B组

5.购物单

查看代码

 #include <iostream>
using namespace std;
int main()
{
  // 请在此输入您的代码
  double sum = 180.90*0.88+10.25*0.65+56.14*0.9+104.65*0.9+100.30*0.88+297.15*0.5+26.75*0.65+130.62*0.5+240.28*0.58+270.62*0.8+115.87*0.88+247.34*0.95+73.21*0.9+101.00*0.5+79.54*0.5+278.44*0.7+199.26*0.5+12.97*0.9+166.30*0.78+125.50*0.58+84.98*0.9+113.35*0.68+166.57*0.5+42.56*0.9+81.90*0.95+131.78*0.8+255.89*0.78+109.17*0.9+146.69*0.68+139.33*0.65+141.16*0.78+154.74*0.8+59.42*0.8+85.44*0.68+293.70*0.88+261.79*0.65+11.30*0.88+268.27*0.58+128.29*0.88+251.03*0.8+208.39*0.75+128.88*0.75+62.06*0.9+225.87*0.75+12.89*0.75+34.28*0.75+62.16*0.58+129.12*0.5+218.37*0.5+289.69*0.8;
  int a = (int)(sum+100)/100*100;
  printf("%d",a);
  return 0;
}

考点：将数据输入进去看有几个100-->52个100

答案：5200

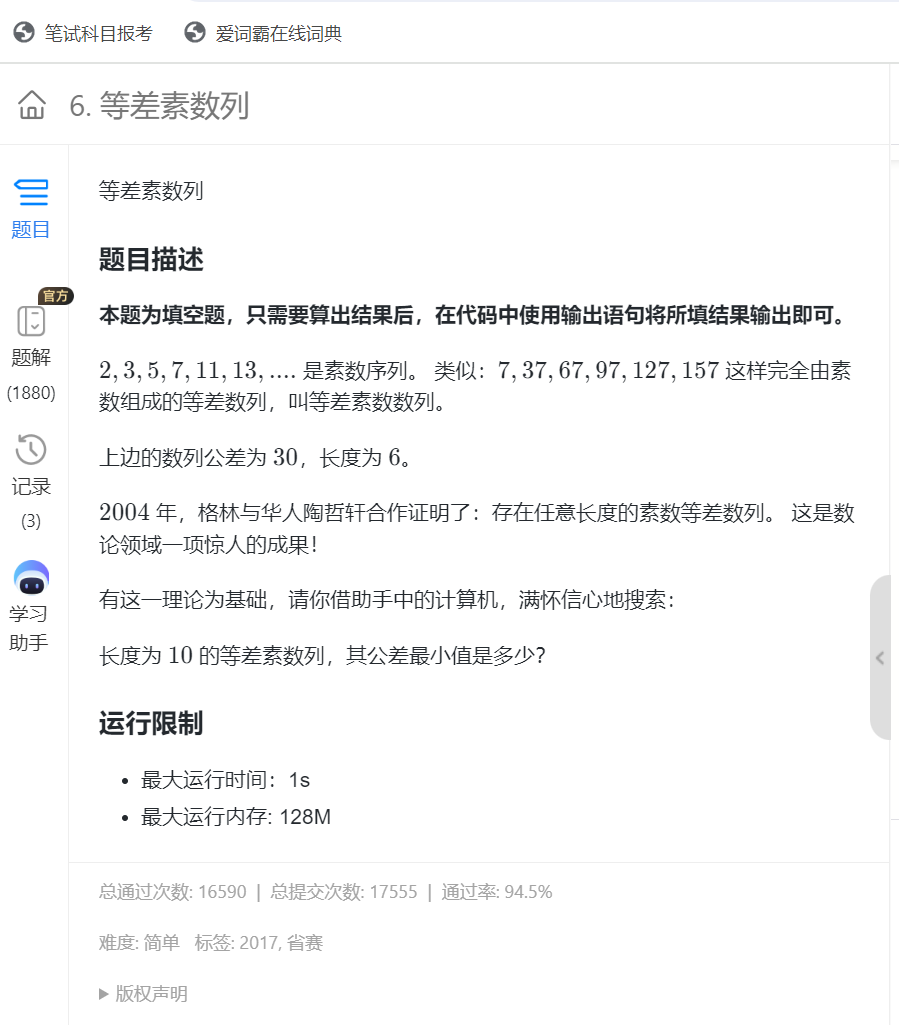
6.等差素数列

#include <bits/stdc++.h>

using namespace std;

typedef long long int ll;

const int N=5000;

ll a[N];

set<ll>all;

//判素数

bool is_prime(ll t){

for(int i=2;i*i<=t;i++){

if(t%i==0)return false;

}

return true;

}

首项公差项数

找最小公差等差素数列

ll f(){

for(int i=0;i<5000;i++){//枚举首项

ll fir=a[i];

//枚举公差

for(int del=2;del<a[4999]-a[fir];del++){//公差不可能大于最大项-当前首项

int m=fir;

for(int j=1;j<10;j++){//枚举项数（要找10项所以从首项往后9项）

m+=del;

if(all.find(m)==all.end())break;//找不到

if(j==9)return del;//找到了，因为加了9项公差如果找不到早返回！

}

return -1;

}

int main()

{

all.insert(2);

all.insert(3);

a[0]=2;

a[1]=3;

int id=2;

ll h=5;

//先打表a素数列，a数组存放5000个素数，all集合存放5000以内所有素数

while(id<5000){

if(is_prime(h)){

all.insert(h);

a[id++]=h;

}

h++;

}

cout<<f();//公差

// 请在此输入您的代码

return 0;

}

注意：

不能用

因为lower_bound找大于等于不能严格控制等于

lower_bound(a,a+n,m)==n-->这个表示找不到m因为找到最后一个下标n-1的后一个即n

因为只是一个填空题可以直接暴力：法二

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+6;
bool ss(int a){//判断素数 
	if(a<2)return false;//不是素数 
	for(int i=2;i<=sqrt(a);i++){
		if(a%i==0)return false;
	}
	return true;
}
int main(){
for(int q=2;q<=N;q++) {
	if(!ss(q))continue;
	for(int d=1;d<=N;d++){//公差
	bool flag=true;
	for(int j=2;j<=10;j++) {
		int t=q+(j-1)*d;
		if(!ss(t)){
			flag=false;
			break;
		}
	}
	if(flag==true)	{
		cout<<d;
		return 0;
	}
	}
}
	return 0;
}

set的用法

set<int> q; //以int型为例默认按键值升序

set<int,greater<int>> p; //降序排列

int x;

q.insert(x); //将x插入q中

q.erase(x); //删除q中的x元素,返回0或1,0表示set中不存在x

q.clear(); //清空q

q.empty(); //判断q是否为空，若是返回1，否则返回0

q.size(); //返回q中元素的个数

q.find(x); //在q中查找x，返回x的迭代器，若x不存在，则返回指向q尾部的迭代器即 q.end()

q.lower_bound(x); //返回一个迭代器，指向第一个键值不小于x的元素

q.upper_bound(x); //返回一个迭代器，指向第一个键值大于x的元素

q.rend(); //返回第一个元素的的前一个元素迭代器

q.begin(); //返回指向q中第一个元素的迭代器

q.end(); //返回指向q最后一个元素下一个位置的迭代器

q.rbegin(); //返回最后一个元素

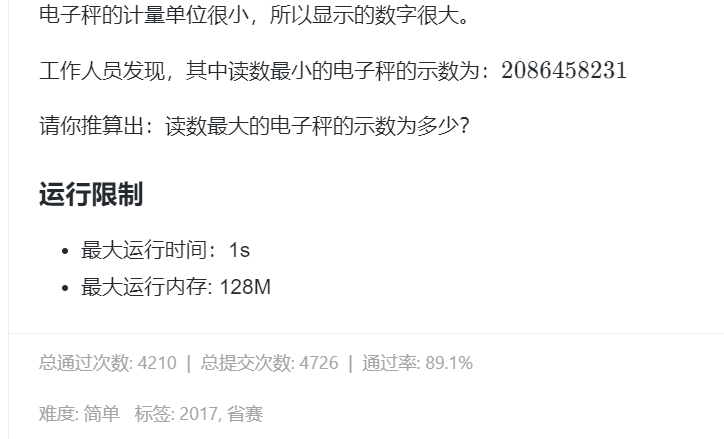
7.承压计算

算法：动态规划（类似于数字三角形）

这个是上面的两个物品一定均分给下面一个物体（这不是dp不是取最值走）

#include<bits/stdc++.h>

using namespace std;

//29行有数

const int N=35;

int a[N][N];

double dp[N][N];

int main(){

for(int i=1;i<=29;i++){

for(int j=1;j<=i;j++){

cin>>a[i][j];

}

dp[1][1]=a[1][1];

for(int i=2;i<=30;i++ ){

for(int j=1;j<=i;j++){

dp[i][j]=a[i][j]+0.5*(dp[i-1][j]+dp[i-1][j-1]);

}

double m=dp[30][1];

double s=dp[30][1];

for(int i=2;i<=30;i++){

if(m<dp[30][i]){

m=dp[30][i];

}

if(s>dp[30][i]){

s=dp[30][i];

}

long long int t=m*(2086458231*1.0/s);//注意精度问题，如果用double当位数太多会出现e的多少次方-->科学计数法！

cout<<t;

return 0;

}

4.方格分割

考点：dfs

#include<bits/stdc++.h>

using namespace std;

int vis[10][10];// 标记是否访问过

int ans;

int dx[4] ={-1,0,0,1};//行标变化(上左右下）

int dy[4] ={0,-1,1,0}; //列标变化(上左右下）

void dfs(int a,int b){

//（1）到边界说明该路线结束ans++

if(a==0||a==6||b==0||b==6){

ans++;

return ;

}

//（2）访问该点

vis[a][b]=1;

vis[6-a][6-b]=1;//剪一刀对称的那边也剪了

//（3）四个方向走

for(int i=0;i<4;i++){

//当前点四个方向走

int nx=a+dx[i];

int ny=b+dy[i];

if(nx<0||nx>6||ny<0||ny>6){

//超过边界

continue;

}

if(!vis[nx][ny]){

//没访问过

dfs(nx,ny) ;

}

//恢复现场

vis[a][b]=0;

vis[6-a][6-b]=0;

}

int main()

{

dfs(3,3);//从中心点（3,3）开始搜，因为剪是中心对称剪！

cout<<ans/4; //注意旋转对称算一次，所以四个方向除以4.

return 0;

}

总结

dfs大部分是求有多少种情况-->搜索

步骤

访问该点（bool变量true）

dfs递归

恢复现场（bool变量false）

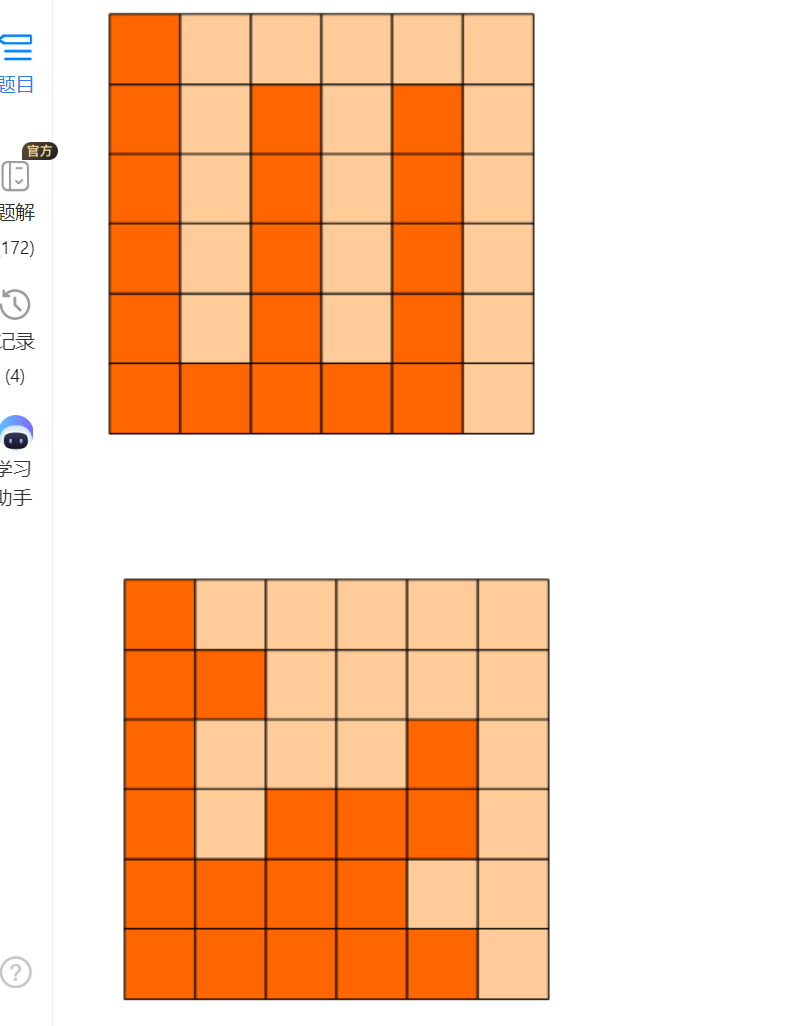
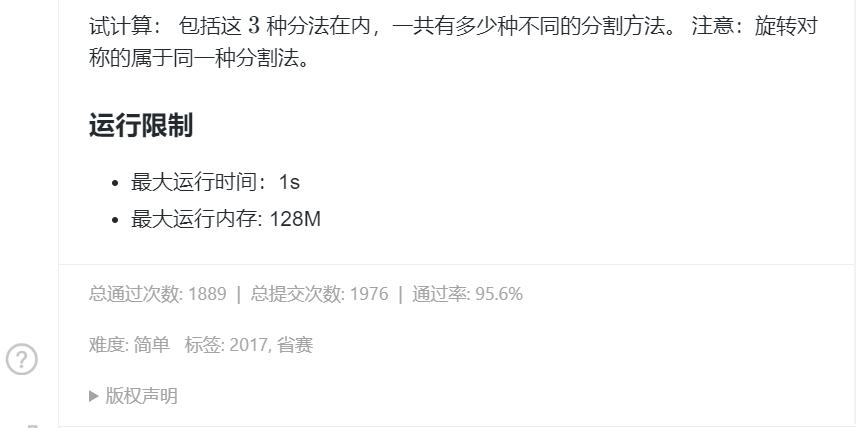
法二

 #include <iostream>
using namespace std;
bool vis[40][40];
int ans;
int dx[]={-1,1,0,0};//上下左右
int dy[]={0,0,-1,1};//列
void dfs(int x,int y){
  //剪的是点,如果一端剪到底说明他对称点那端也到底就说明剪完
if(x==0||x==6||y==0||y==6){
  ans++;
  return ;
}
  for(int i=0;i<4;i++){
    int nx=x+dx[i];
    int ny=y+dy[i];
    if(x==0||x==6||y==0||y==6){
 continue;
}
if(!vis[nx][ny]){
vis[nx][ny]=true;
vis[6-nx][6-ny]=true;
dfs(nx,ny);
vis[nx][ny]=false;
vis[6-nx][6-ny]=false;
}
  }

}
int main()
{
  vis[3][3]=true;
  dfs(3,3);//从中间点，因为要求剪出来的两部分完全相同即中心对称
cout<<ans/4;//四个方向旋转对称
  return 0;
}

题目：取数位

考察：递归

#include<bits/stdc++.h>
using namespace std;
//计算位数
int len(int x){
if(x<10)return 1;//1位数
return len(x/10) +1;
}
//计算第k位数
int f(int x,int k ){
if(len(x)-k==0)return x%10;//末位数
return f(x/10,k);//答案
}
int main(){
int x=23574;
cout<<f(x,3);
return 0;
}

题目：最大公共子串

#include <stdio.h>

#include <string.h>

#define N 256

int f(const char* s1, const char* s2)

{

int a[N][N];

int len1 = strlen(s1);

int len2 = strlen(s2);

int i,j;

memset(a,0,sizeof(int)*N*N);

int max = 0;

for(i=1; i<=len1; i++){

for(j=1; j<=len2; j++){

if(s1[i-1]==s2[j-1]) {

a[i][j] = __________________________; //填空

if(a[i][j] > max) max = a[i][j];

}

return max;

}

int main()

{

printf("%d\n", f("abcdkkk", "baabcdadabc"));

return 0;

}

答案： a[i][j] =a[i-1][j-1]+1;

考动态规划转移方程->意思是公共子串到s1的第i位和s2的第j位匹配的长度为公共子串到s1的第i-1位和s2的第j-1位的长度+1

所以s1[i-1]==s2[j-1]下标比位置小1.

2.日期问题

#include<bits/stdc++.h>

using namespace std;

struct sj{

int n;

int y;

int r;

}a[3];

//比较函数

bool com(sj p,sj q){

if(p.n!=q.n)return p.n<q.n;//早的放前面

if(p.y!=q.y)return p.y<q.y;

return p.r<q.r;

}

int year;

bool ir() {

if((year%4==0&&year%100!=0)||(year%400==0))return true;

return false;

}

int cn(int h){

if(h>=0&&h<=59)year=2000+h;

else{

year=1900+h;

}

return year;

}

//月

bool cy(int m){

if(m>=1&&m<=12)return true;

return false;

}

//日

bool cr (int m,int n){//m月n日

if(m==1||m==3||m==5||m==7||m==8||m==10||m==12) {

if(n>=1&&n<=31)return true;

}

if(m==4||m==6||m==9||m==11){

if(n>=1&&n<=30)return true;

}

if(m==2){

if(ir()){

if(n>=1&&n<=29)return true;

}

else{

if(n>=1&&n<=28)return true;

}

return false;

}

int main(){

string s;

cin>>s;

int AA=(s[0]-'0')*10+(s[1]-'0');

int BB=(s[3]-'0')*10+(s[4]-'0');

int CC=(s[6]-'0')*10+(s[7]-'0');

int cnt=0;

// 1.年月日

year=cn(AA);//返回年份

if(cy(BB)){

if(cr(BB,CC)){

a[cnt].n=year;

a[cnt].y=BB;

a[cnt].r=CC;

cnt++;

}

//2.月日年

year=cn(CC);//返回年份

if(cy(AA)){

if(cr(AA,BB)){

a[cnt].n=year;

a[cnt].y=AA;

a[cnt].r=BB;

cnt++;

}

//3.日月年

year=cn(CC);//返回年份

if(cy(BB)){

if(cr(BB,AA)){

a[cnt].n=year;

a[cnt].y=BB;

a[cnt].r=AA;

cnt++;

}

sort(a,a+cnt,com) ;//从小到大

for(int i=0;i<cnt;i++){

//去重

if(i>0){

if(a[i].n==a[i-1].n&&a[i].y==a[i-1].y&&a[i].r==a[i-1].r)continue;

}

cout<<a[i].n<<'-';

if(a[i].y<10)cout<<'0'<<a[i].y<<'-';

else {

cout<<a[i].y<<'-';

}

if(a[i].r<10)cout<<'0'<<a[i].r;

else{

cout<<a[i].r;

}

cout<<endl;

}

return 0;

}

分巧克力

二分例题：

儿童节那天有 $K$

小明拿出了珍藏的巧克力招待小朋友们。

小明一共有 $N$

为了公平起见，小明需要从这 $N$

切出的巧克力需要满足：

形状是正方形，边长是整数
大小相同

例如一块 $6 \times 5$

当然小朋友们都希望得到的巧克力尽可能大，你能帮小明计算出最大的边长是多少么？

输入格式

第一行包含两个整数 $N$

以下 $N$

输入保证每位小朋友至少能获得一块 $1 \times 1$

输出格式

输出切出的正方形巧克力最大可能的边长。

数据范围

$1 \leq N, K \leq 10^{5}$

输入样例：

2 10
6 5
5 6

输出样例：

题目解析：

首先由每一位小朋友所得巧克力边长相同-->我们要求的就是满足条件的一个值（最大边长）-->对于每一块巧克力豆花粉乘若干块这个边长的小巧克力

所以关键就是求一个值

所以很容易想到二分算法

开始进行二分操作

1.check函数

我们要满足的是巧克力分出来的个数>=小朋友数

所以需要满足的条件是for循环所有巧克力划分出来的子块数求和>=小朋友数

每一块巧克力在确定划分边长是x时能划分出（h[i]/x)*(w[i]/x)个子块

2.写左右边界

最终答案介于1~10⁵

l=1

r=1e5

3.写while循环

while（l<r）{

int mid=l+r+1>>1;//由下面的l，r变化-->确定mid上取整

if(check(mid)){

//划分块多了那么需要增加边长

l=mid;

}

else{

r=mid-1;

}

4.输出答案l

cout<<l;

完整代码

 #include<bits/stdc++.h>
using namespace std;
int n,k;//n块巧克力，k个小朋友
const int N=1e5+6;
int h[N];//所有巧克力的长
int w[N];//所有巧克力的宽
typedef long long int ll;
bool check(int x){
    ll res=0;
    for(int i=0;i<n;i++){
        res+=(ll)(h[i]/x)*(w[i]/x);
    }
    if(res>=k)return true;
    return false;
}
int main(){
    cin>>n>>k;
    for(int i=0;i<n;i++)cin>>h[i]>>w[i];
    //进行二分（先定l，r然后不断通过check函数（满足什么条件）来找到想要的值）
   //巧克力边长至少为1
    int l=1;
    //巧克力边长最多为10的5次方
    int r=1e5;
    while(l<r){
        int mid=l+r+1>>1;
        if(check(mid)){
            l=mid;
        }
        else r=mid-1;
    }
    cout<<l;
    return 0;
}

posted @ 2024-04-04 09:13 Annaprincess 阅读(34) 评论(0) 收藏举报

刷新页面返回顶部

luckyyaoyao

2017省赛蓝桥杯B组

2017省赛蓝桥杯B组

5.购物单

6.等差素数列

set的用法

7.承压计算

4.方格分割

题目：取数位

题目：最大公共子串

2.日期问题

分巧克力

二分例题：

输入格式

输出格式

数据范围

输入样例：

输出样例：

公告