2019蓝桥杯省赛B组
2019蓝桥杯省赛B组
A.组队

方法一:人脑计算(每次选最大,但是一个人不能当两个位)
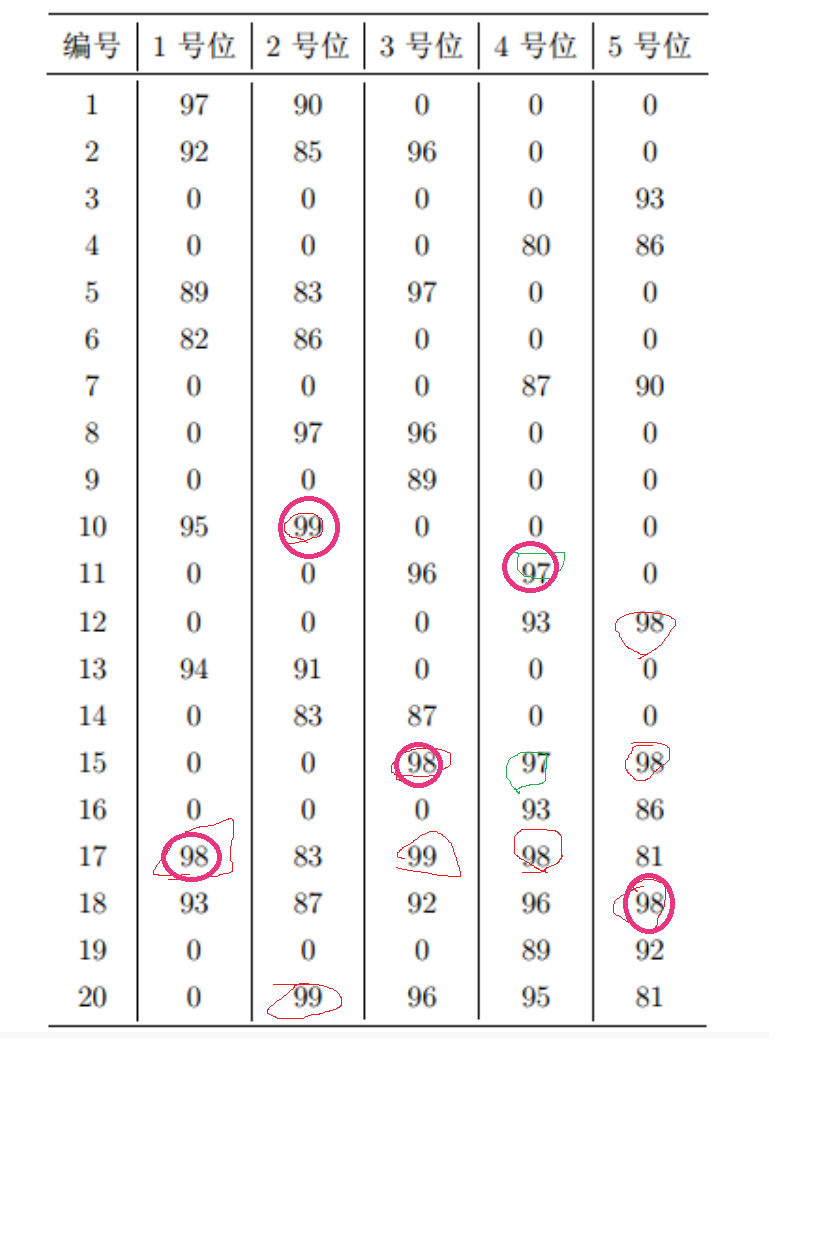
最大值:98+99+98+97+98
法二:枚举
#include <bits/stdc++.h>
using namespace std;
int a[5][20];
int ans;
bool vis[5];//这个人有没有访问过
void dfs(int dep,int t){
if(dep==5){
ans=max(ans,t);
return ;
}
for(int i=0;i<20;i++){
if(!vis[i]){
vis[i]=true;
dfs(dep+1,t+a[dep][i]);
vis[i]=false;
}
}
}
int main()
{
for(int i=0;i<5;i++){//5个位置
for(int j=0;j<20;j++){ //每个位置上20个人的成绩
cin>>a[i][j];
}
}
dfs(0,0);
cout<<ans;
return 0;
}B.年号子串
C.数列求值

//考点:类似斐波拉契数列+取模运算
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
int main(){
ll a=1;
ll b=1;
ll c=1;
for(int i=4;i<=20190324;i++){
ll t=c%10000;
c=(a+b+c)%10000;
a=b%10000;
b=t%10000;
}
cout<<c%10000;
return 0;
}D.数的分解

using namespace std;
typedef long long int ll;
ll ans;
bool check(int a){
while(a){
if(a%10==2||a%10==4)return true;
a/=10;
}
return false;
}
int main(){
for(int i=1;i<=2019;i++){
if(check(i)) continue;
for(int j=i+1;j<=2019;j++){
if(check(j))continue;
for(int p=j+1;p<=2019;p++){
if(check(p))continue;
if(i+j+p==2019)ans++;
}
}
}
cout<<ans;
return 0;
}
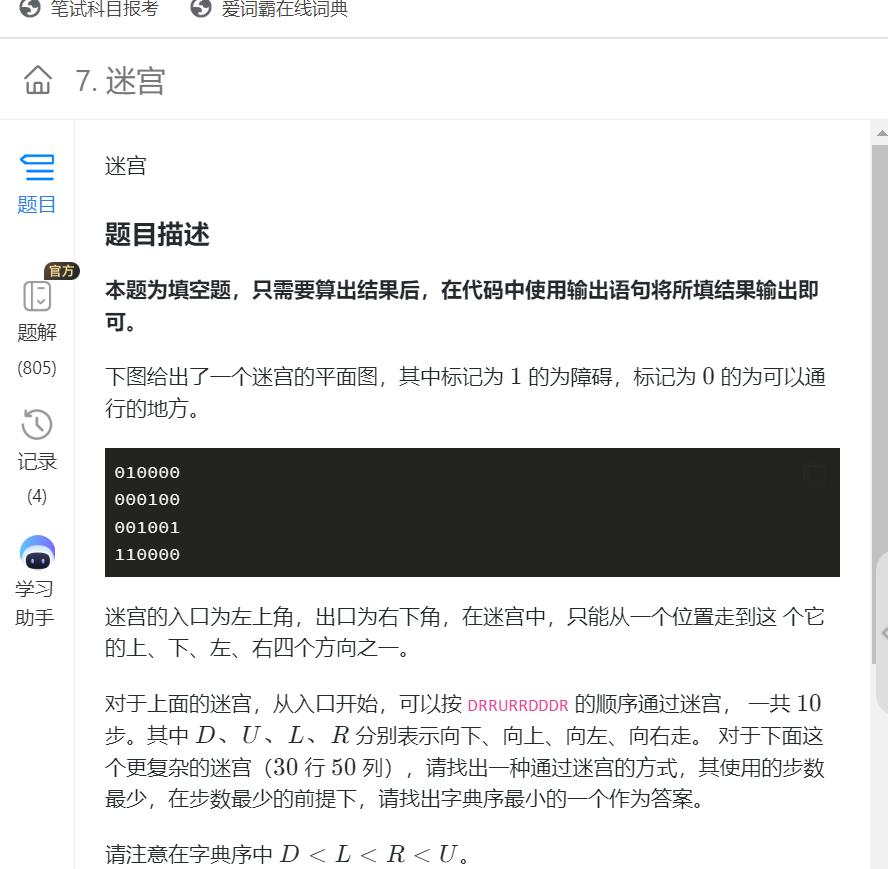
E.迷宫(有问题)

F.特别数的和
考察:筛选

G.完全二叉树的权值
考点:暴力枚举
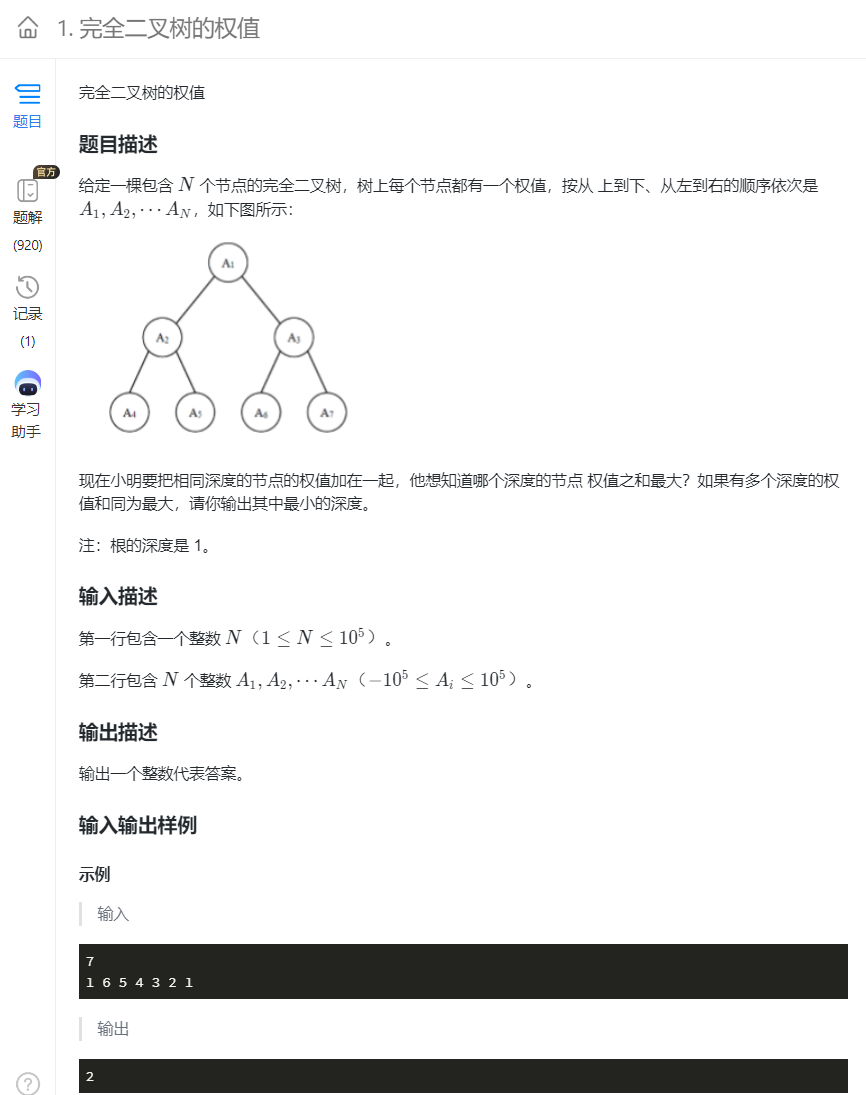
完全二叉树只有可能最后一层不满,全满的叫满二叉树!
H.等差数列
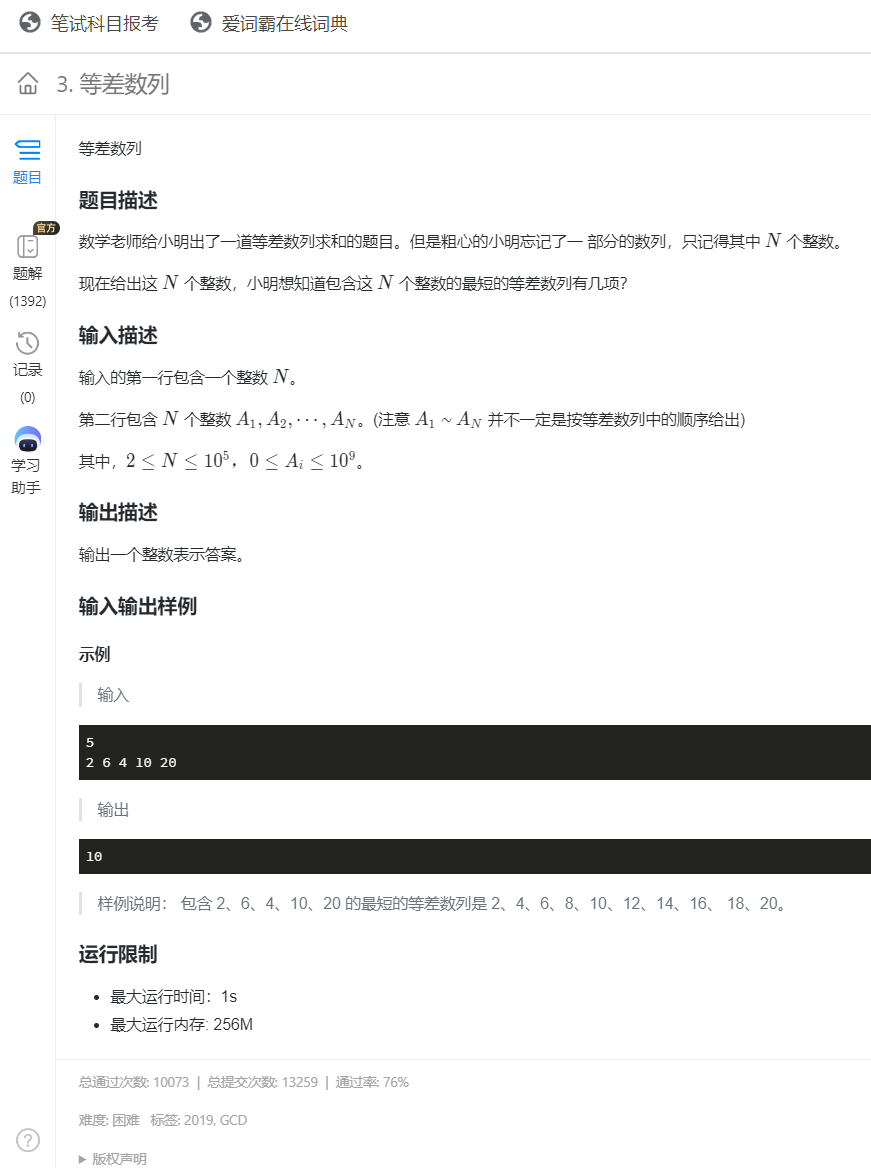
考察算法:最大公公因数gcd
思路:
现将数列从小到大排
然后相邻元素差值计算出来,并且求得差值的最大公因数作为数列的公差
最后根据an=a1 +(n-1)*d
所求的n=(an-a1)/d+1
I.后缀表达式

#include <bits/stdc++.h>
using namespace std;
int main()
{
int n,m;
cin>>n>>m;
int k=n+m+1;
int a[200010];
for(int i=0;i<k;i++)cin>>a[i];
sort(a,a+k);
long long int res=0;
if(!m){
for(int i=0;i<k;i++){
res+=a[i];
}
}
else{
res=a[k-1]-a[0];
for(int i=1;i<k-1;i++){
res+=abs(a[i]);
}
}
cout<<res;
// 请在此输入您的代码
return 0;
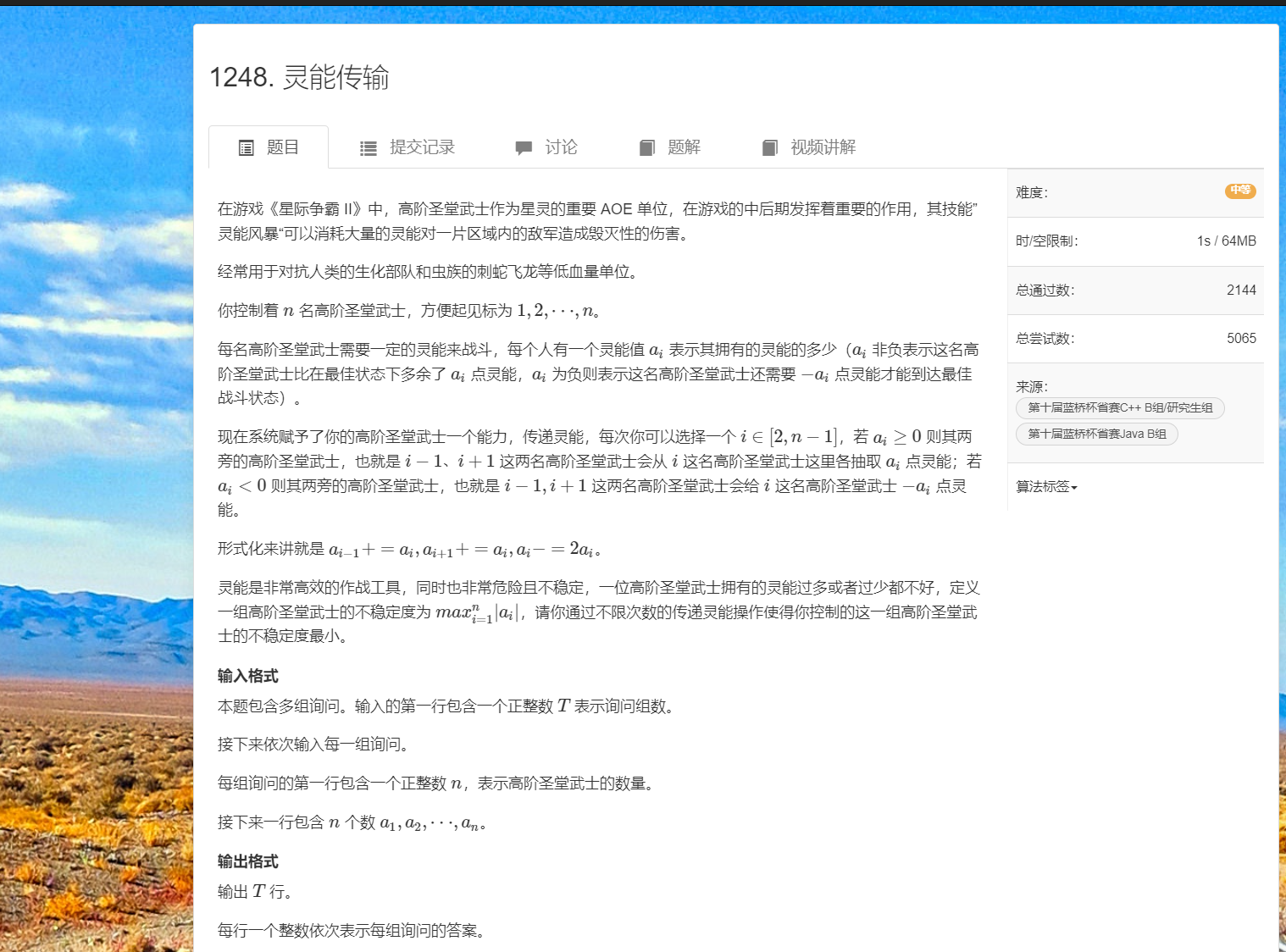
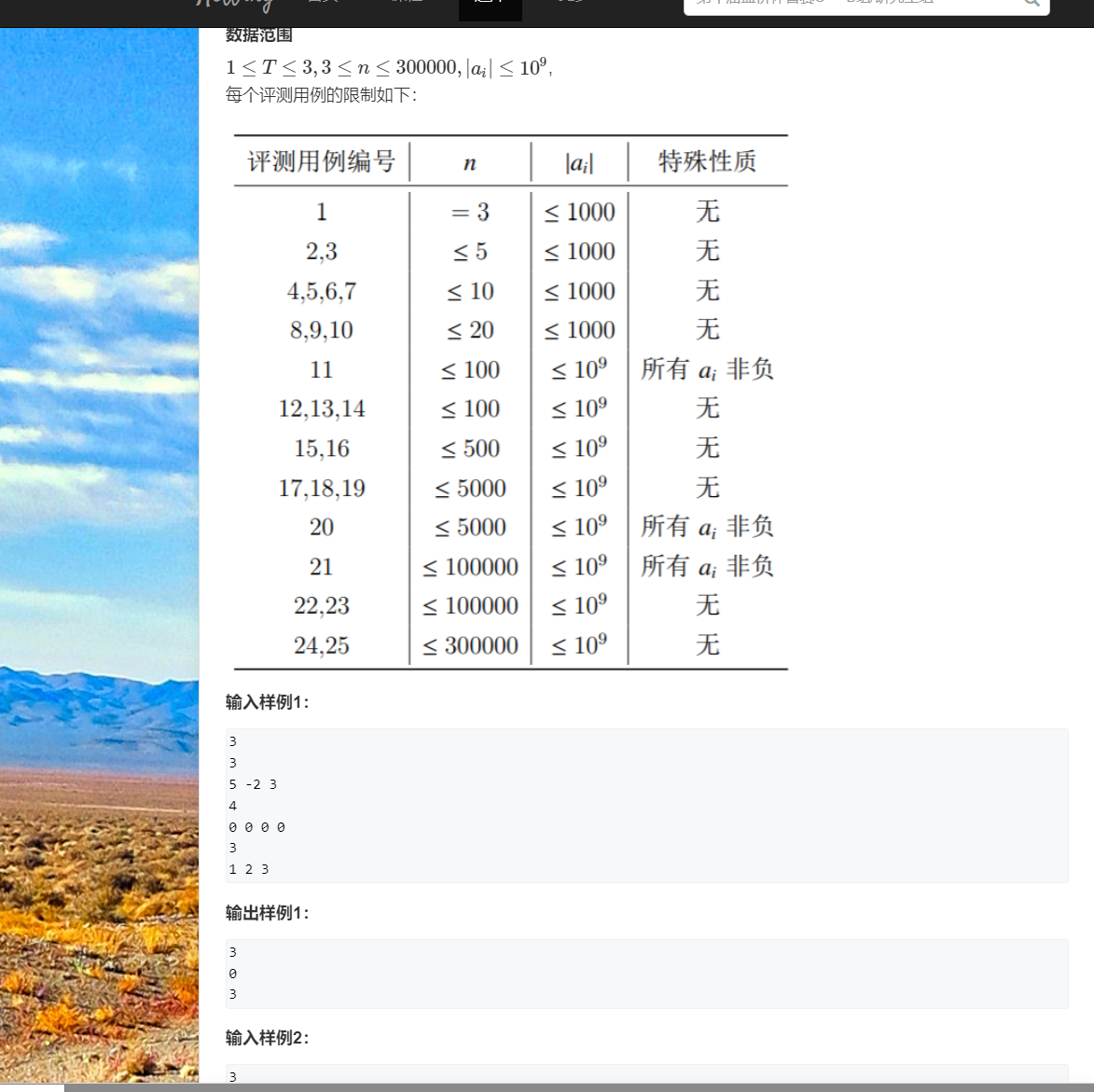
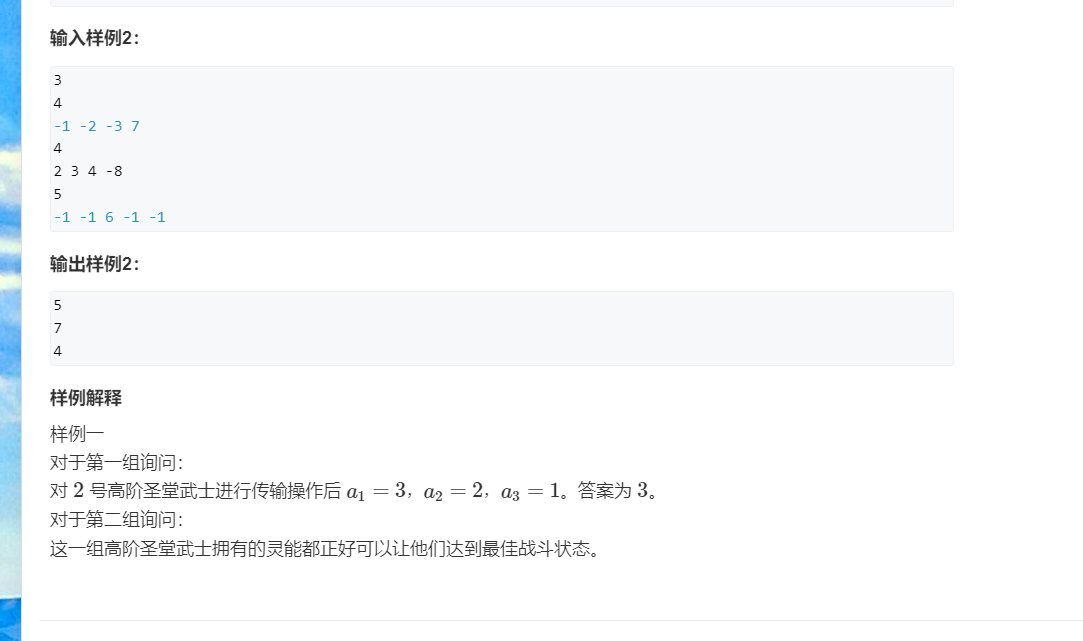
}J.灵能传输
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 300010;
int n;
LL a[N], s[N];
bool st[N];
int main()
{
int T;
scanf("%d", &T);
while (T -- )
{
//每一组实验做一次前缀和
scanf("%d", &n);
s[0] = 0;
for (int i = 1; i <= n; i ++ )
{
scanf("%lld", &a[i]);
s[i] = s[i - 1] + a[i];
}
LL s0 = s[0], sn = s[n];//边界值
if (s0 > sn) swap(s0, sn);//为了统一为s0<sn,因为是对称的所以考虑一直情况即可。
sort(s, s + n + 1);//排序数组,0~n
//现在数列升序
//找寻s0第一次出现的下标值(因为按升序排列数组,原位置可能变动,因为s0可能等于sn,所以s0取前一个,sn取后一个。下面是确定他们的新下标。
for (int i = 0; i <= n; i ++ )
if (s[i] == s0)
{
s0 = i;
break;
}
for (int i = n; i >= 0; i -- )
if (s[i] == sn)
{
sn = i;
break;
}
memset(st, 0, sizeof st);
int l = 0, r = n;
//最前面一段
for (int i = s0; i >= 0; i -= 2)
{
a[l ++ ] = s[i];
st[i] = true;
}
//最后面一段
for (int i = sn; i <= n; i += 2)
{
a[r -- ] = s[i];
st[i] = true;
}
中间段(不重复走)
for (int i = 0; i <= n; i ++ )
if (!st[i])
a[l ++ ] = s[i];
LL res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, abs(a[i] - a[i - 1]));//存放结果准备好,所以最优选项就是当前这么摆,所以只有求相邻前缀和的差即求得当前数字值,然后取max的abs差值!
printf("%lld\n", res);//结果
}
return 0;
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号