动态规划

0~1背包

题目描述https://www.luogu.com.cn/problem/P1048

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入格式

第一行有个整数 $T$ （ $1 \leq T \leq 1000$ ）和 $M$ （ $1 \leq M \leq 100$ ），用一个空格隔开， $T$ 代表总共能够用来采药的时间， $M$ 代表山洞里的草药的数目。

接下来的 $M$ 行每行包括两个在到之间（包括和）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式

输出在规定的时间内可以采到的草药的最大总价值。

输入输出样例

输入 #1

输出 #1

说明/提示

【数据范围】

对于的数据， $M \leq 10$ ；
对于全部的数据， $M \leq 100$ 。

【题目来源】

NOIP 2005 普及组第三题

查看代码

//0~1背包 
#include<bits/stdc++.h>
using namespace std;
 
int t[111],w[111];
int dp [1110];
int main(){
	//时间有限
	int  T,M;
	cin>>T>>M;//时间，草药的数量
	for(int i=1;i<=M;i++) cin>>t[i]>>w[i];
	for(int i=1;i<=M;i++){
		for(int j=T;j>=t[i];j--){
		dp[j]=max(dp[j],dp[j-t[i]]+w[i]);	
		}
	}
	cout<<dp[T];
	return 0;
}

注意事项：

数组容量：

t,w数组容量用多少种

dp一维数组剩下那维度[ ] 里存放时间，所以开个1000以上，因为时间最大1000

题目背景https://www.luogu.com.cn/problem/P1164

uim 神犇拿到了 uoi 的 ra（镭牌）后，立刻拉着基友小 A 到了一家……餐馆，很低端的那种。

uim 指着墙上的价目表（太低级了没有菜单），说：“随便点”。

题目描述

不过 uim 由于买了一些书，口袋里只剩 $M$ 元 $(M \leq 10000)$ 。

餐馆虽低端，但是菜品种类不少，有 $N$ 种 $(N \leq 100)$ ，第 $i$ 种卖 $a_{i}$ 元 $(a_{i} \leq 1000)$ 。由于是很低端的餐馆，所以每种菜只有一份。--->0~1背包

小 A 奉行“不把钱吃光不罢休”，所以他点单一定刚好把 uim 身上所有钱花完。他想知道有多少种点菜方法。

由于小 A 肚子太饿，所以最多只能等待秒。

输入格式

第一行是两个数字，表示 $N$ 和 $M$ 。

第二行起 $N$ 个正数 $a_{i}$ （可以有相同的数字，每个数字均在以内）。

输出格式

一个正整数，表示点菜方案数，保证答案的范围在 int 之内。

输入输出样例

输入 #1

4 4
1 1 2 2

输出 #1

说明/提示

2020.8.29，增添一组 hack 数据 by @yummy

查看代码

 #include<bits/stdc++.h>
using namespace std;
int m,n;
int a[120];
int dp[1100];//花费i元的方案数 
int main(){
	cin>>n>>m;//n种，m元，1种1个
	dp[0]=1;
	 for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
	
	for(int j=m;j>=a[i];j--) {
		dp[j]+=dp[j-a[i]];
	}
}
	cout<<dp[m];
	return 0;
}

考察点：0~1背包

简直是价值

转换方程：dp[j]=dp[j]+dp[j-a[i]];

dp[j]表示花费j元的方案数，

dp[j]包含两部分

（1）花费j元时第i件物品没买

dp[j]

(2)花费j元时第i件物品买

dp[j-a[i]]

题目描述

给出一个长度为

输入格式

第一行是一个整数，表示序列的长度

第二行有

输出格式

输出一行一个整数表示答案。

输入输出样例

输入 #1

7
2 -4 3 -1 2 -4 3

输出 #1

说明/提示

样例 1 解释

选取

数据规模与约定

对于
对于

查看代码

 #include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const int N=2e5+6;
ll a[N];
ll dp[N];
int main(){
ll n;
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++){
	dp[i]=max(a[i],dp[i-1]+a[i]);
}
int m=dp[1];
for(int i=1;i<=n;i++){
	if(m<dp[i])m=dp[i];
}
cout<<m;
return 0;
}

动态规划转换方程：

dp[i]=max(dp[i-1]+a[i],a[i])

因为是连续的子段和，dp[i]表示以第i个元素结尾的最大子段和，所以最大要么就是一直到第i个元素最大子段和，要么就是只有第i个元素。

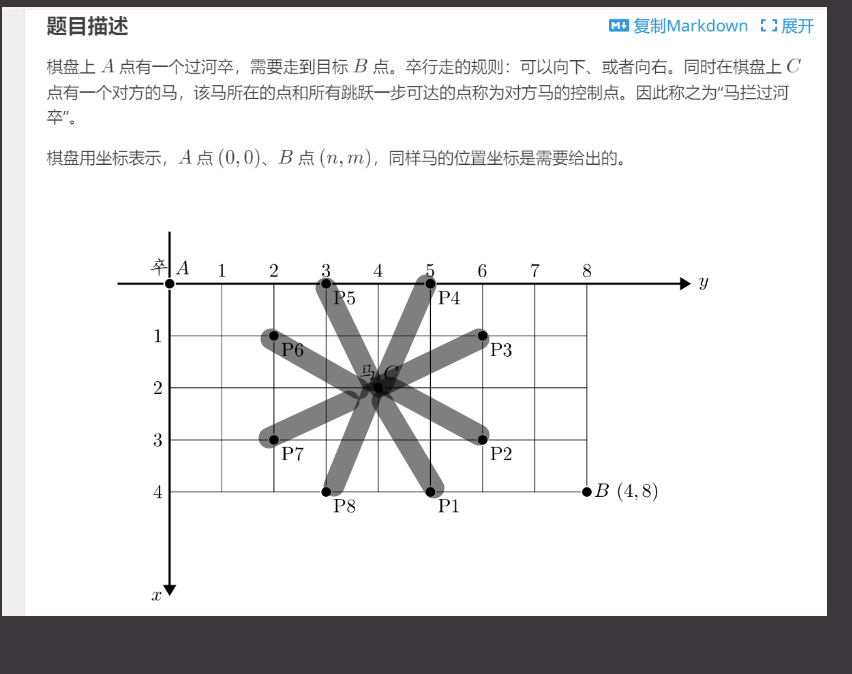
过河卒：P1002 [NOIP2002 普及组] 过河卒 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

查看代码

 #include<bits/stdc++.h> 
using namespace std;
long long int dp[26][26];//到某点的方案数。 
int nf[26][26];//默认0表示为能走 
int main(){
	int xb,yb,x,y;
	cin>>xb>>yb>>x>>y;
	//担心马出界 所以整体向右向下2格 
	xb+=2;
	yb+=2;
	x+=2;
	y+=2;
	
	//不能走--->马走日，以马为中心，呈现日字为不可走nf[ ]为1
	nf[x] [y]=1;
	nf[x-2][y-1]=1;
	nf[x-2][y+1]=1;
	nf[x-1][y-2]=1;
	nf[x-1][y+2]=1;
	nf[x+2][y-1]=1;
	nf[x+2][y+1]=1;
	nf[x+1][y-2]=1;
	nf[x+1][y+2]=1;
	//起点(0,0)变成（2,2） 
	dp[1][2]=1;//为了让新起点（2,2）的方案数为1，那么初始化 dp[1][2]=1或dp[2][1]=1 
	for(int i=2;i<=xb;i++) {
		for(int j=2;j<=yb;j++){
			if(nf[i][j]==1) continue;
			dp[i][j]=dp[i-1][j]+dp[i][j-1];
		}
	}
	cout<<dp[xb][yb];
	return 0; 
}

装箱问题：（0~1背包）

P1049 [NOIP2001 普及组] 装箱问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

查看代码

//0~1背包 
#include<bits/stdc++.h>
using namespace std;
int v[40] ;//当前物品体积
int dp[20010];//dp[i]表示背包体积为i时能放入最大的体积
int w[40];//当前物品体积，当做权重
int main(){
int V;
cin>>V;
int n;
cin>>n;
for(int i=1;i<=n;i++)	{
	cin>>v[i];
	w[i]=v[i];
}

for(int i=1;i<=n;i++)
{
	for(int j=V;j>=v[i];j--){
		dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
	}
}
cout<<(V-dp[V]);//最小剩余体积=背包总体积-背包所能放入最大体积

return 0;
}

五倍经验日：

题目背景

现在乐斗有活动了！每打一个人可以获得 5 倍经验！absi2011 却无奈的看着那一些比他等级高的好友，想着能否把他们干掉。干掉能拿不少经验的。

题目描述

现在 absi2011 拿出了 $x$ 个迷你装药物（嗑药打人可耻…），准备开始与那些人打了。

由于迷你装药物每个只能用一次，所以 absi2011 要谨慎的使用这些药。悲剧的是，用药量没达到最少打败该人所需的属性药药量，则打这个人必输。例如他用 $2$ 个药去打别人，别人却表明 $3$ 个药才能打过，那么相当于你输了并且这两个属性药浪费了。

现在有 $n$ 个好友，给定失败时可获得的经验、胜利时可获得的经验，打败他至少需要的药量。

要求求出最大经验 $s$ ，输出 $5 s$ 。

输入格式

第一行两个数， $n$ 和 $x$ 。

后面 $n$ 行每行三个数，分别表示失败时获得的经验 $l o s e[_{i}$ ，胜利时获得的经验 $w i n[_{i}$ ]和打过要至少使用的药数量 $u s e[_{i}$ 。

输出格式

一个整数，最多获得的经验的五倍。

输入输出样例

输入 #1

输出 #1

说明/提示

【Hint】

五倍经验活动的时候，absi2011 总是吃体力药水而不是这种属性药。

【数据范围】

对于的数据，保证 $x = 0$ 。
对于的数据，保证 $0 \leq n \leq 10$ ， $0 \leq x \leq 20$ 。
对于的数据，保证 $0 \leq n, x \leq 100$ ， $0 < l o s e[_{i]}, w i n[_{i} \leq 100$ ， $0 \leq u s e[_{i} \leq 5$ 。
对于的数据，保证 $0 \leq n, x \leq 1 0^{3}$ ， $0 < l o s e_{i} \leq w i n_{i} \leq 1 0^{6}$ ， $0 \leq u s e_{i} \leq 1 0^{3}$ 。

【题目来源】

fight.pet.qq.com

absi2011 授权题目

三种代码：

第一种代码

查看代码

//0~1背包 
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+6;
int lose[N];
int win[N];
int use[N];
long long int dp[N];

int main(){
long long	int s=0;

	int n,x;
	cin>>n>>x;
	for(int i=1;i<=n;i++)cin>>lose[i]>>win[i]>>use[i];
    for(int i=1;i<=n;i++ ){
    	for(int j=x;j>=use[i];j--)
          dp[j]=max(dp[j]+lose[i],dp[j-use[i]]+win[i]);
         for(int j=use[i]-1;j>=0;j--)
          dp[j]+=lose[i];
	}
	s=dp[x];

	
	cout<<5*s;
	return 0;
}

第二种代码

查看代码

 //0~1背包 
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+6;
int lose[N];
int win[N];
int use[N];
long long int dp[N][N];

int main(){
long long	int s=0;

	int n,x;
	cin>>n>>x;
	for(int i=1;i<=n;i++)cin>>lose[i]>>win[i]>>use[i];
    for(int i=1;i<=n;i++ ){
    	for(int j=0;j<=x;j++){
    		dp[i][j]=dp[i-1][j]+lose[i];
    		if(j-use[i]>=0){
    			dp[i][j]=max(dp[i][j],dp[i-1][j-use[i]]+win[i]);
			}
		}
	}
	s=dp[n][x];

	
	cout<<5*s;
	return 0;
}

第三种代码

查看代码

//0~1背包 
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+6;
int lose[N];
int win[N];
int use[N];
long long int dp[N];

int main(){
long long	int s=0;

	int n,x;
	cin>>n>>x;
	for(int i=1;i<=n;i++)cin>>lose[i]>>win[i]>>use[i];
    for(int i=1;i<=n;i++ ){
    for(int j=x;j>=0;j--) {
    	//没战胜 
    	
    	if(j>=use[i]){
    		dp[j]=max(dp[j]+lose[i],dp[j-use[i]]+win[i]);
		}
		else{
			dp[j]=dp[j]+lose[i];
		}
	}
	}
	s=dp[x];

	
	cout<<5*s;
	return 0;
}

if(j>=use[i]){

dp[j]=max(dp[j]+lose[i],dp[j-use[i]]+win[i]);

}

else{

dp[j]=dp[j]+lose[i];

}

应该先写j>=use[i]情况

总结：

这三种代码：转换方程--->对于取第i件用dp[j-use[i]]+win[i]，不取第i件用dp[j]+lose[i]--->要加上lose

注意0~1背包内层循环变量由大到小

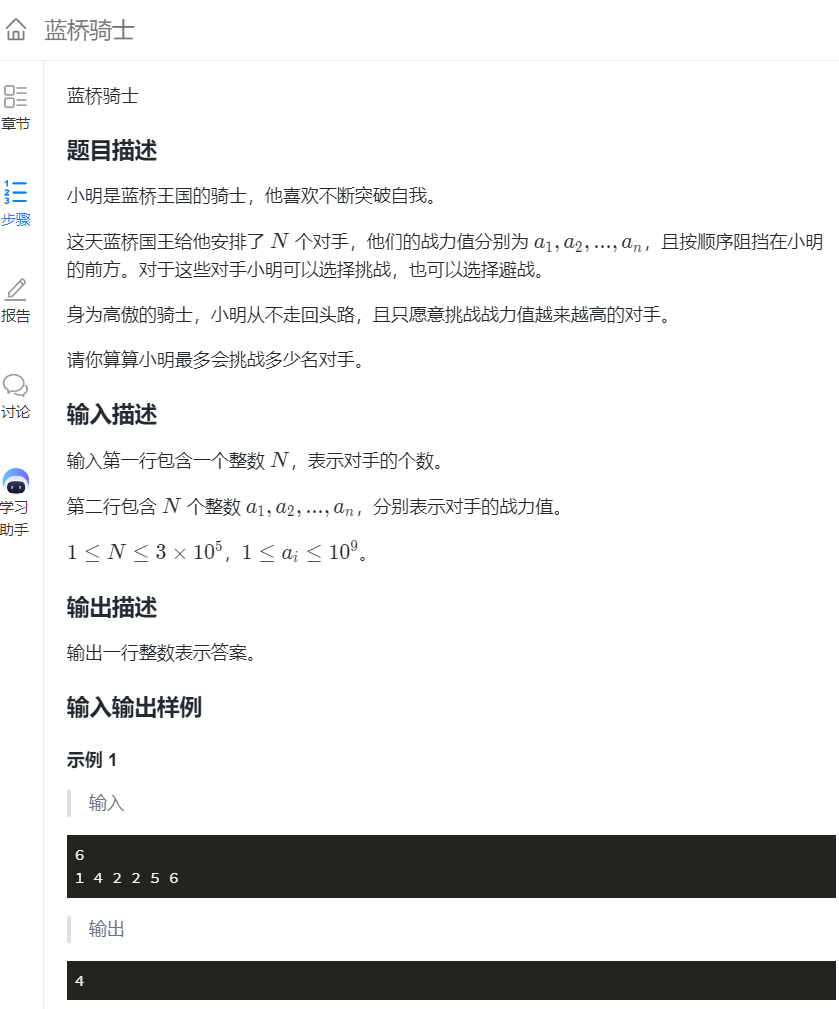
蓝桥骑士

https://www.lanqiao.cn/courses/21965/learning/?id=1149641&compatibility=false

#include <bits/stdc++.h>
using namespace std;
int arr[300009];
int low[300009];
int main()
{
    int N;
    int length=1;
    cin>>N;
    for(int i=1;i<=N;i++)cin>>arr[i];    
    low[1]=arr[1];//初始化，长度为1的子序列初始化为第一个元素 
    for(int i=2;i<=N;i++)//依次遍历后面的元素，更新low数组 
    {
        if(arr[i]>low[length])//若当前元素大于low数组末尾元素，直接插入 
        {
            low[++length]=arr[i];
        }
        else//若小于，则用low数组中刚好大于等于它的元素替换之 
        {
            int index=lower_bound(low+1,low+1+length,arr[i])-low;//获取插入位置下标 
            low[index]=arr[i];//替换 
        }
    }
    cout<<length<<endl;//输出low数组长度即为答案 
    return 0;
}

posted @ 2024-02-04 08:29 Annaprincess 阅读(16) 评论(0) 收藏举报

刷新页面返回顶部

luckyyaoyao

动态规划

动态规划

题目描述https://www.luogu.com.cn/problem/P1048

输入格式

输出格式

输入输出样例

说明/提示

题目背景https://www.luogu.com.cn/problem/P1164

题目描述

输入格式

输出格式

输入输出样例

说明/提示

题目描述

输入格式

输出格式

输入输出样例

说明/提示

样例 1 解释

数据规模与约定

过河卒：P1002 [NOIP2002 普及组] 过河卒 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

装箱问题：（0~1背包）

五倍经验日：

题目背景

题目描述

输入格式

输出格式

输入输出样例

说明/提示

三种代码：

总结：

蓝桥骑士

公告

luckyyaoyao

动态规划

动态规划

题目描述https://www.luogu.com.cn/problem/P1048

输入格式

输出格式

输入输出样例

说明/提示

题目背景https://www.luogu.com.cn/problem/P1164

题目描述

输入格式

输出格式

输入输出样例

说明/提示

题目描述

输入格式

输出格式

输入输出样例

说明/提示

样例 1 解释

数据规模与约定

过河卒 ：P1002 [NOIP2002 普及组] 过河卒 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

装箱问题：（0~1背包）

五倍经验日：

题目背景

题目描述

输入格式

输出格式

输入输出样例

说明/提示

三种代码：

总结：

蓝桥骑士

公告

过河卒：P1002 [NOIP2002 普及组] 过河卒 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)