2021第十二届蓝桥杯省赛
2021第十二届蓝桥杯省赛
填空题:
1.计算空间(考察单位转换)
k=10^3 Kilo(千)
M=10^6 Mega(百万)
G=10^9 Giga(十亿)
T=10^12 Tera(兆)
P=10^15 Peta(千兆)
E=10^18 Exa(百京)
B=10^21 Bronto(十垓)
1TB=1024GB
1GB=1024MB
1MB=1024KB
1KB=1024Byte
注:Byte就是B也就是字节
KB是千字节
MB是兆
GB是千兆
TB是千千兆
https://www.lanqiao.cn/problems/1445/learning/?subject_code=1&group_code=4&match_num=12&match_flow=1&origin=cup
思路:
256MB=256*210 *210 B
32位=32/8=4B
所以答案是:(256*210 *210 )/4
9.货物摆放
https://www.lanqiao.cn/problems/1463/learning/?subject_code=1&group_code=4&match_num=12&match_flow=1&origin=cup

长宽高肯定是n的因子。
暴力枚举三重循环长宽高都从1~n然后当长*宽*高=n时ans+=1一定会超时
长宽高枚举都是从n的因子中取所以先求因子。
输出答案:
#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;
vector<ll>t;//存放n的因子
int main()
{
ll ans=0;
ll n;
cin>>n;
ll h=sqrt(n+0.5);//向上取整开方
//找n的所有因子
for(int i=1;i<=h;i++){
if(n%i==0){
t.push_back(i);
if(i*i==n)continue;
else t.push_back(n/i);
}
}
//t[i],t[j],t[k]为长宽高
for(int i=0;i<t.size();i++){
for(int j=0;j<t.size();j++){
for(int k=0;k<t.size();k++){
if(t[i]*t[j]*t[k]==n)ans+=1;
}
}
}
cout<<ans;
// 请在此输入您的代码
return 0;
}
8.路径
https://www.lanqiao.cn/problems/2383/learning/?subject_code=1&group_code=4&match_num=12&match_flow=1&origin=cup
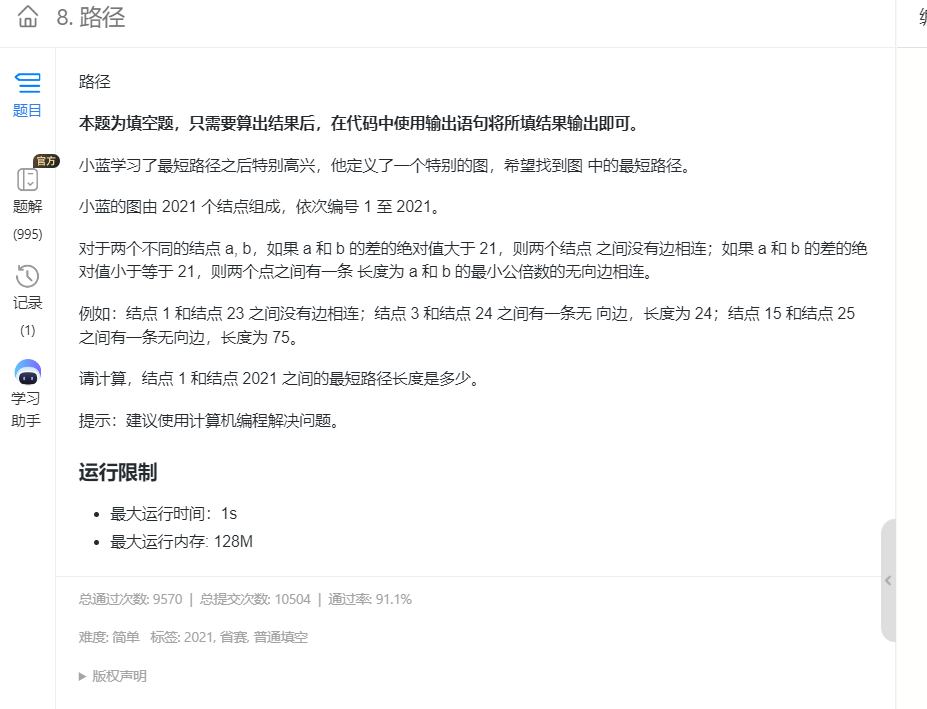
答案:
cout<<10266837;
计算思路:
考察算法:
最短路算法+最小公倍数算法
最短路算法任选一个下面是迪杰斯特拉算法
i,j最小公倍数=i*j/gcd(i,j);
gcd为最大公因数算法
自环在最短路里没有用可不管
重边取最小
//朴素版djstla
#include<bits/stdc++.h>
using namespace std;
const int N=2100;
int n,m;//n个顶点m条边
int g[N][N];//每条边的权值
bool st[N];//st[i]表示第i个点已经访问
int d[N] ; //本题中st[i]为从第一个点到第i个点的最小值
int djs(){
memset(d,0x3f,sizeof(d));
d[1]=0;//到自己距离是 0
for(int i=0;i<n-1;i++)//找n-1回
{
int t=-1;//为找寻那个可以确定的点
for(int j=1;j<=n;j++){
if((!st[j])&&(t==-1||d[t]>d[j])){
t=j;
}
}
//用找到的t那个点尝试更新所有点如果能使距离减小
for(int j=1;j<=n;j++){
d[j]=min(d[j],d[t]+g[t][j]);
}
st[t]=true;
}
if(d[n]==0x3f3f3f3f)return -1;
else return d[n];
}
int gcd(int a,int b){
if(b==0)return a;
else return gcd(b,a%b);
}
int main(){
n=2021;
memset(g,0x3f,sizeof(g));
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(abs(i-j)<=21)g[i][j]=(i*j)/gcd(i,j);
}
}
cout<<djs();
return 0;
}
3.直线
https://www.lanqiao.cn/problems/1449/learning/?subject_code=1&group_code=4&match_num=12&match_flow=1&origin=cup


#include<bits/stdc++.h>
using namespace std;
bool h[21];
bool l[21];
// 求最大公约数
int gcd(int a, int b) {
return b == 0? a : gcd(b, a % b);
}
int main() {
int num = 0;
set<pair<pair<int, int>, int>> ans;
for (int i = 0; i <= 19; i++) {
for (int j = 0; j <= 20; j++) {
for (int x = 0; x <= 19; x++) {
for (int y = 0; y <= 20; y++) {
if (i == x && j == y) continue;
if (j == y) {
if (!h[j]) {
h[j] = true;
num++;
}
continue;
}
if (i == x) {
if (!l[i]) {
num++;
l[i] = true;
}
continue;
}
int dx = x - i;
int dy = y - j;
int d = gcd(dx, dy);
dx /= d;
dy /= d;
int intercept = j * dx - i * dy;
ans.insert({{dx, dy}, intercept});
}
}
}
}
cout << ans.size() + num << endl;
return 0;
}浮点数精度问题一般少用除法,可以同时去分母
程序题:
10.卡片问题
https://www.lanqiao.cn/problems/2383/learning/?subject_code=1&group_code=4&match_num=12&match_flow=1&origin=cup

Ck2+k>=n
#include <bits/stdc++.h>
using namespace std;
int main()
{
//k^2+k>=2n
int n;
cin>>n;
int ans;
for(int i=1;i<=sqrt(2*n);i++){
if(i*i+i>=2*n){
ans=i;
break;
}
}
cout<<ans;
return 0;
}#include <iostream>
using namespace std;
const long long int N=100006;
//数组容量有限制最多开10的八次方
//所以要对总数最大值公式求解S=n+Cn 2 =n+(n*(n-1))/2=(n+n*n)/2
//所以开个10的五次方即可
//d[i]表示i种牌的最大搭配人数,转移方程:dp[i]=dp[i-1]+i 第i种牌可以和前i-1种牌或自己本身搭配
long long int d[N];
int n;
int main()
{
cin>>n;
int i;
for( i=1;;i++){
d[i]=d[i-1]+i;
if(d[i]>=n)break;
}
cout<<i;
// 请在此输入您的代码
return 0;
}4.时间显示
https://www.lanqiao.cn/problems/1452/learning/?subject_code=1&group_code=4&match_num=12&match_flow=1&origin=cup

G.砝码称重


算法分析:dp
状态表示:
f[i][j]表示取到第i个砝码可以称出来质量为j,称出来为true,否则为false
状态转移方程:思考从取到第i-1个怎么转移到取到第i个砝码且称出来质量为j
有三种转移情况->默认左物右码,所以右边+左边-
1.不取第i个物品
f[i-1][j]
2.第i个物品放在天平右边
f[i-1][j-w[i]]
3.第i个物品放在天平左端
f[i-1][j+w[i]]
三种转移情况取或因为只要任意一个满足就能转移到f[i][j]
二重循环:
外:遍历i从取1个到取到第n个
内:遍历j从0~m,m为能称出的最大质量
注意:
1.j+w[i]<=m因为遍历时j最大为m那么j+w[i]会超过m要防止
2.数组下标>=0所以j-w[i]取abs绝对值
3.注意dp初始化f[0][0]=true;//一个没取称到的质量为0
最后遍历所有可能质量1~m看f[n][i]是否为true即取到最后一个砝码能否达到当前质量。
H.杨辉三角

算法考点:
1.组合数-->会求Cr k
2.二分-->找到正确位置
分析:

易知:杨辉三角关于中间对称轴对称所以求最早出现位置只看左边
斜着看会发现从上到下递增,从左往右看中间最大,向外递减
所以最早位置的最佳选取是中间轴上,中间轴满足Ca 2a 从a=0开始
一定能找到一个位置因为Cn1=n最差位置
代码分析:
J.括号序列

考点:动态规划
思考:
1.增加左右括号方法相互独立,所以添加左括号有l种方案,添加右括号有r种,所以总方案数l*r
2.计算l的方法r方法类似(对称)
所以计算完l后
翻转字符串并且将左括号变右括号,右括号变左括号
I.双向排序


分析:
1.第一个有效操作是降序。
2.连续的降序或者是连续的升序只保留区间最长的那次操作
3.所以由2可以得降序升序交替进行
4.有效的前缀区间长是严格减小的,有效的后缀区间长是严格减小的
代码分析:
#include<bits/stdc++.h>
//定义pair的两项
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;//第一维存操作数,第二维存处理区间端点,对应题目中p,q
const int N = 100010;
int n, m;
PII stk[N];//用栈存放操作
int ans[N];//用数组存结果
int main()
{
scanf("%d%d", &n, &m);
int top = 0;
对于有效操作的处理
while (m -- )
{
int p, q;
scanf("%d%d", &p, &q);
if (!p)//降序
{
while (top && stk[top].x == 0) q = max(q, stk[top -- ].y);//连续降序q取最大
while (top >= 2 && stk[top - 1].y <= q) top -= 2;//不连续降序交替出现,所以从栈中删除那些降序区间小于q的还有升序,所以top-2
stk[ ++ top] = {0, q};//从栈下标为1开始存,将处理后的入栈
}
else if (top)//注意第一个有效操作不能是后缀升序
{//升序
while (top && stk[top].x == 1) q = min(q, stk[top -- ].y);
while (top >= 2 && stk[top - 1].y >= q) top -= 2;
stk[ ++ top] = {1, q};
}
}
int k = n, l = 1, r = n;//左右端点l,r.k负责计数
//入录答案核心
for (int i = 1; i <= top; i ++ )
{
if (stk[i].x == 0)
while (r > stk[i].y && l <= r) ans[r -- ] = k -- ;
else
while (l < stk[i].y && l <= r) ans[l ++ ] = k -- ;
if (l > r) break;
}
//多余
if (top % 2)
while (l <= r) ans[l ++ ] = k -- ;
else
while (l <= r) ans[r -- ] = k -- ;
for (int i = 1; i <= n; i ++ )
printf("%d ", ans[i]);
return 0;
}
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
const int N=100010;
typedef pair<int,int>PII;
PII st[N];//栈存放p,q
int ans[N];//存放答案
int main(){
int n,m;
int top=0;
cin>>n>>m;//长度为n,操作m次
while(m--){
int p,q;
cin>>p>>q;
if(!p){//前缀降序
while(top&& st[top].x==0){//连续的降序
q=max(q ,st[top--].y);//栈顶弹出
}
while(top>=2&&st[top-1].y<=q){//交替降序升序
top-=2;//top为升序,top-1为
}
//入栈
st[++top]={0,q};
}
//升序,并且栈非空,因为第一个有效操作是降序
else if(top){
while(top&& st[top].x==1){//连续升序
q=min(q, st[top--].y);
}
while(top>=2&& st[top-1].y>=q){//交替升降序,top为降序,top-1为升序
top-=2;
}
//入栈
st[++top]={1,q};
}
}
//入录答案
int k=n;//计数
int l=1;//左端点
int r=n;//右端点
for(int i=1;i<=top;i++){
//从第一个操作开始,第一个有效操作前缀降序
if (st[i].x==0){
while(l<=r&&r> st[i].y){//前缀降序。间接的说明后面半段从右向左降序,r> st[i].y千万别取等。
ans[r--]=k--;
}}
else{
while(l<=r&& st[i].y>l){//后缀升序,间接说明左边半段从左到右降序,因为有效操作从降序开始。st[i].y>l请问别取等。
ans[l++]=k--;
}}
if(l>r)break;//定义循环的出口
}
//多余部分
if(top%2){
//多个降序操作,因为操作的顺序降升降升...
while(l<=r){ans[l++]=k--;}
}
else{
//多个升序
while(l<=r){
ans[r--]=k--;
}
}
//输出答案
for(int i=1;i<=n;i++){
cout<<ans[i]<<" ";
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号