二维动态规划+子集和

题目：

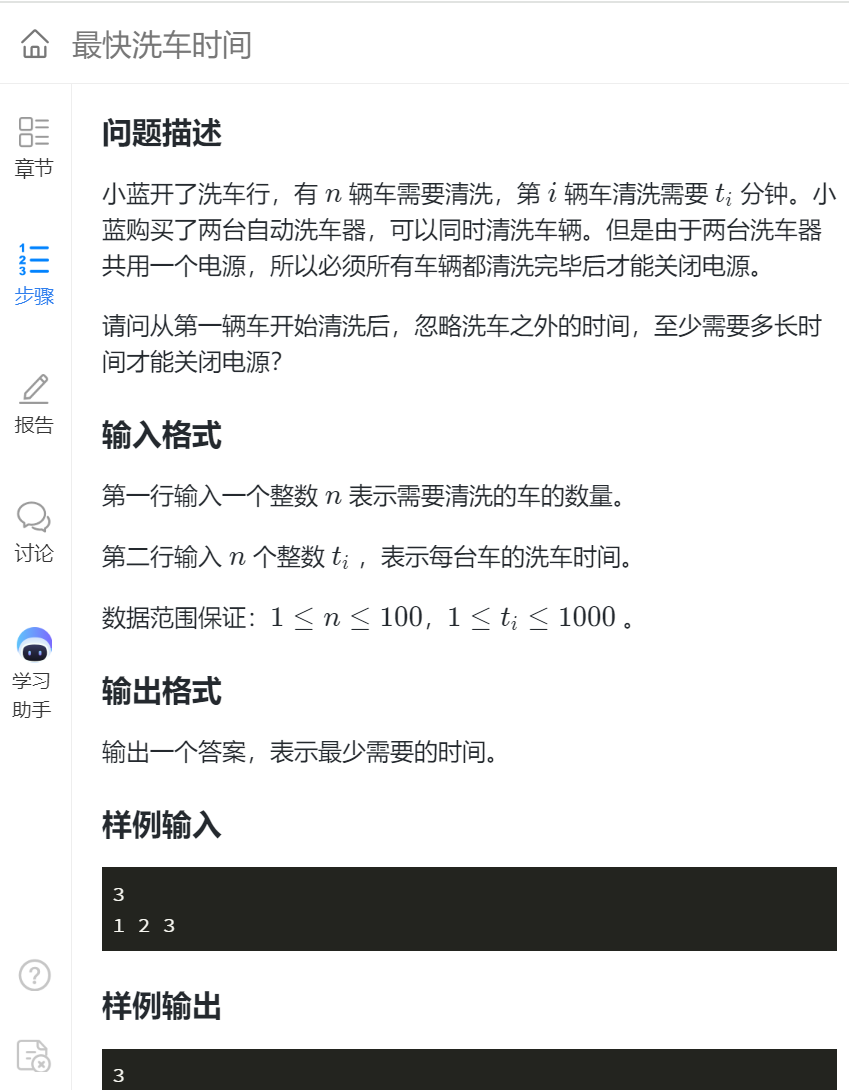
查看代码

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e3+7;
const ll mod = 1e5+7;
int n, s;
int dp[N][N], a[N];

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n;
    for(int i = 1; i <= n; ++ i)
    {
        cin >> a[i];
        s += a[i];//总时间
    }
    dp[0][0] = 1;
    for(int i = 1; i <= n; ++ i)
    {
        for(int j = 1; j <= s; ++ j)
        {
            dp[i][j] = dp[i-1][j] | dp[i-1][j-a[i]];//表示i台车，j分钟，第二种要第i台
        }
    }
    int ans = mod;
    for(int i = 1; i <= s; i ++)
    {
        if(dp[n][i])
        {
//选择两台机器中数值大的
            ans = min(ans, max(i, s-i));
        }
    }
    cout << ans << '\n';
    return 0;
}

方法 2维dp：

首先计算总时间s（这个是最大的时间不可能超过）

dp[0][0]初始化为1

然后用子集和即并集 

然后动态规划方程：

是一个并集方程

  dp[i][j] = dp[i-1][j] | dp[i-1][j-a[i]];//表示i台车，j分钟，第二种要第i台

 dp[i][j] 表示到第i辆车用时为j可以由两种情况转移而来

（1）dp[i-1][j]不包括第i辆车用时为j

（2）dp[i-1][j-a[i]]加上第i辆车用时才到j，所以i-1辆车用时为j-a[i]

最后计算最小时间

从二者取最小

从已求ans和当前两台机器各洗时间最大值取最小

ans = min(ans, max(i, s-i));

此时的i表示当前洗衣机用时，s-i表示另个洗衣机用时！