题解 UVA1193 【Radar Installation】

传送门

题意

对于第 $i$ 组测试数据，在一条数轴上选一些点，用以这些点为圆心作的半径为 $d$ 的圆覆盖所给点，若无法全部覆盖，则输出 Case i: -1；否则输出 Case i: $+$ 最少需要的点数 $ans$。

分析

为了方便，我们把 $x$ 和 $y$ 都存在结构体 $asdf$ 中。

struct asdf
{
	int x,y;
	double l,r;//这个后面会讲
}a[N];

我们首先判断是否能全部覆盖，一个点能够被数轴上的某个点覆盖，当且仅当它与数轴的距离 $a_i.y$ 不超过半径 $d$，所以我们输入的时候判断一下就好了。

t++;//第t组测试数据 
b=0;//b代表是否有点没被覆盖 
for(int i=1;i<=n;i++)
{
	cin>>a[i].x>>a[i].y;
	if(a[i].y>d)//y就是第i个点到数轴的距离
	{
		b=1;//标记 
		break;//已经有不能覆盖的点就不做无用的输入了 
	}
}
if(b)//有没被覆盖的点 
{
	cout<<"Case "<<t<<": -1"<<endl;
	continue;
}

接下来，我们预处理出距离第 $i$ 个点不超过 $d$ 的最左点 $a_i.l$ 和最右点 $a_i.r$，这样当我们想判断某个点上装的雷达时候能覆盖到第 $i$ 个点的时候，只要判断是否在 $a_i.l$ 到 $a_i.r$ 的线段上就行了。

那么 $a_i.l$ 怎么求呢？请看下图：

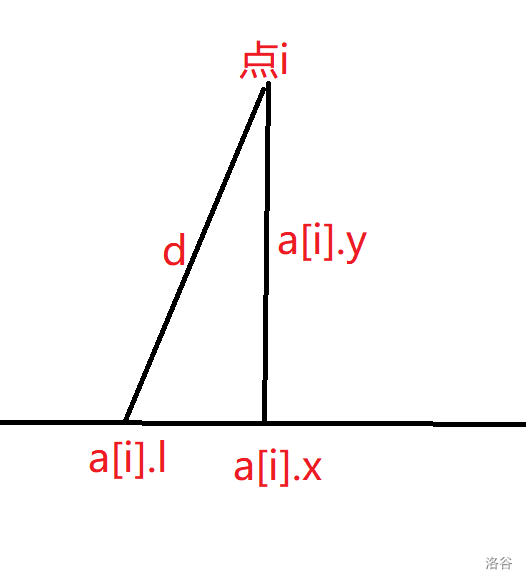
如图所示，$d、a_i.y$ 和 $(a_i.x-a_i.l)$ 正好构成了一个直角三角形，根据小学时学过的勾股定理：

$$a_i.y^2+(a_i.x-a_i.l)^2=d^2$$

反过来就是：

$$a_i.l=a_i.x-\sqrt{d^2+a_i.y^2}$$

$a_i.r$ 也同理：

$$a_i.r=a_i.x+\sqrt{d^2+a_i.y^2}$$

for(int i=1;i<=n;i++)
{
	a[i].l=a[i].x-sqrt(d*d-a[i].y*a[i].y);
	a[i].r=a[i].x+sqrt(d*d-a[i].y*a[i].y);
}

然后就是贪心了，设上一个雷达的位置为 $w$，我们按 $x$ 轴从小到大排序，当前我们在第 $i$ 个点，则我们有以下 $2$ 种选择：

$1.$ 让当前的点被之前的雷达覆盖。

$2.$ 新建一个雷达供它使用。

我们为了使雷达最少，在条件允许的情况下应该尽量选择第一种，条件就是当前雷达位置 $w$ 比不少于能覆盖第 $i$ 个点的最左点 $a_i.l$，即 $w>=a_i.l$，不过有可能当前雷达位置 $w$ 超过了能覆盖第 $i$ 个点的最右点 $a_i.r$，我们只能把雷达向左移一些满足要求，即 $w=\min(w,a_i.r)$。

如果不能选择第一种，那么我们只能选择第二种了，为了给后面留出更多的位置，我们把雷达尽量往右放，又要覆盖这个点，所以只能放在能覆盖第 $i$ 个点的最右点 $a_i.r$，即 $w=a_i.r$，且 $ans$ 要加 $1$，因为我们又放了一个雷达。注意，第一个点时还没有雷达，所以我们在第一个点直接放雷达，然后循环 $2-n$。

sort(a+1,a+n+1,cmp);//排序
w=a[1].r;ans=1;//第一个点直接放雷达 
for(int i=2;i<=n;i++)//循环剩下的n-1次 
{
	if(w>=a[i].l)//能覆盖到 
		w=min(w,a[i].r);//第一种选择 
	else 
		ans++,w=a[i].r;//否则只能第二种选择 
}

代码

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int t,n,d,ans;
bool b;
double w;
struct asdf
{
	int x,y;
	double l,r;
}a[N];
bool cmp(asdf p,asdf q)//按x轴从小到大排序 
{
	return p.x<q.x;
}
int main()
{
    while(cin>>n>>d&&n&&d)//有多组数据 
    {
    	t++;//第t组测试数据 
    	b=0;//b代表是否有点没被覆盖 
    	for(int i=1;i<=n;i++)
    	{
    		cin>>a[i].x>>a[i].y;
    		if(a[i].y>d)//y就是第i个点到数轴的距离
    		{
    			b=1;//标记 
    			break;//已经有不能覆盖的点就不做无用的输入了 
			}
		}
		if(b)//有没被覆盖的点 
		{
			cout<<"Case "<<t<<": -1"<<endl;
			continue;
		}
		for(int i=1;i<=n;i++)
		{
			a[i].l=a[i].x-sqrt(d*d-a[i].y*a[i].y);
			a[i].r=a[i].x+sqrt(d*d-a[i].y*a[i].y);
		} 
		sort(a+1,a+n+1,cmp);//排序
		w=a[1].r;ans=1;//第一个点直接放雷达 
		for(int i=2;i<=n;i++)//循环剩下的n-1次 
		{
			if(w>=a[i].l)//能覆盖到 
				w=min(w,a[i].r);//第一种选择 
			else 
				ans++,w=a[i].r;//否则只能第二种选择 
		}
		cout<<"Case "<<t<<": "<<ans<<endl;
	}
	return 0;
}

懂了来领双倍经验。