CF252A Little Xor

solution 1

此解法复杂度为 $O(n^3)$。

由于数据很小，所以我们暴力枚举左右端点，暴力计算前缀和即可。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n,a[N],mx,sum;
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	for(int i=1;i<=n;i++)
	{
		for(int j=i;j<=n;j++)
		{
			sum=a[i];
			for(int k=i+1;k<=j;k++)
				sum^=a[k];
			mx=max(mx,sum);
		}
	}
	cout<<mx<<endl;
	return 0;
}

如果 $n$ 的范围扩大到 $1000$ 呢？

solution 2

此解法复杂度为 $O(n^2)$。

我们设这个序列为 $a_1,a_2,…,a_n$，$s_i=a_1\ xor\ a_2\ xor\ …\ xor \ a_i=s_{i-1}\ xor\ a_i$，其中 $s_0=0$。

此时， $a_i\ xor\ a_{i+1}\ xor\ …\ xor \ a_j$

$=0\ xor\ (a_i\ xor\ a_{i+1}\ xor\ …\ xor \ a_j)$

$=(a_1\ xor\ a_2\ xor\ …\ xor \ a_{i-1})\ xor\ (a_1\ xor\ a_2\ xor\ …\ xor \ a_{i-1})\ xor\ (a_i\ xor\ a_{i+1}\ xor\ …\ xor \ a_j)$

$=(a_1\ xor\ a_2\ xor\ …\ xor \ a_{i-1})\ xor\ (a_1\ xor\ a_2\ xor\ …\ xor \ a_{i-1}\ xor\ a_i\ xor\ a_{i+1}\ xor\ …\ xor \ a_j)$

$=s_{i-1}\ xor\ s_j$

这就是异或前缀和。

这样我们只要暴力枚举 $i,j$，就只有 $O(n^2)$ 的时间复杂度。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n,a,s[N],mx; 
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
    	cin>>a;
    	s[i]=s[i-1]^a;
	}
	for(int i=1;i<=n;i++)
		for(int j=i;j<=n;j++)
			mx=max(mx,s[j]^s[i-1]);
	cout<<mx<<endl;
	return 0;
}

如果 $n$ 继续扩大到 $10^4,10^5,10^6$ 呢？

solution 3

此解法复杂度为 $O(n)$。

考虑改进 solution 2。

在求出了异或前缀和的前提下，我们的问题变成了：

在给定的 $n+1$ 个整数 $s_0,s_1,s_2,…,s_n$ 中选出两个进行 $xor$（异或）运算，得到的结果最大是多少？

我们考虑所有的二元组 $(i,j)$ 且 $i<j$，那么本题的目标就是在其中找到 $s_i\ xor\ s_j$ 的最大值。也就是说，对于每个 $i(0\le i\le n)$，我们希望找到一个 $j(0\le j<i)$，使 $s_i\ xor\ s_j$ 最大，并求出这个最大值。

我们可以把每个整数看作长度为 $30$ 的二进制 $01$ 串（数值较小时在前面补 $0$），并且把 $s_0～s_{i-1}$ 对应的 $30$ 位二进制串插入一棵 $\text{Trie}$ 树（其中最低二进制位为叶子节点）。

接下来。对于 $s_i$ 对应的 $30$ 位二进制串，我们在 $\text{Trie}$ 中进行一次与检索类似的过程，每一步都尝试沿着“与 $s_i$ 的当前位相反的字符指针”向下访问。若“与 $s_i$ 的当前位相反的字符指针”指问空节点，则只好访问与 $s_i$ 当前位相同的字符指针。根据 $xor$ 运算“相同得 $0$，不同得 $1$”的性质，该方法即可找出与 $s_i$ 做 $xor$ 运算结果最大的 $s_j$。

如下页图所示，在一棵插入了 $2(010),5(101),7(111)$ 三个数的 $\text{Trie}$ 中，分别查询与 $6(110),3(011)$做 $xor$ 运算结果最大的数。（为了简便，图中使用了 $3$ 位二进制数代替 $30$ 位二进制数。）

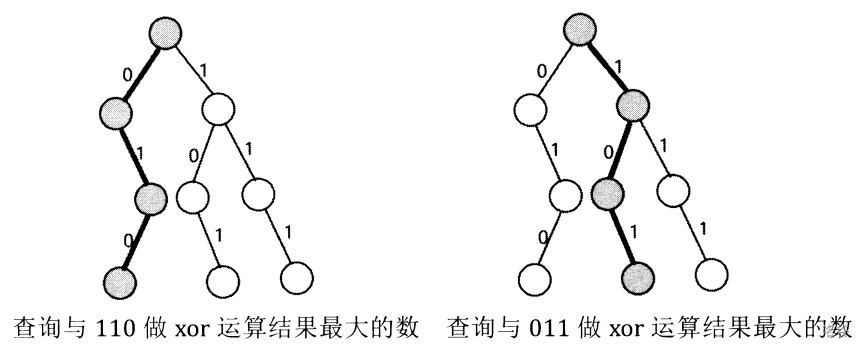
综上所述，我们可以循环 $i=1～n$，对于每个 $i$，$\text{Trie}$ 树中应该存储了 $s_0～s_{i-1}$ 对应的 $30$ 位二进制串（实际上每次 $i$ 增长前，把 $s_i$ 插入 $\text{Trie}$ 即可)。根据我们刚才提到的“尽量走相反的字符指针”的检索策略，就可以找到所求的 $s_j$，更新答案。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n,a,s[N],trie[N*32][2],tot=1,mx;
void Trie_insert(int x)//插入 
{
	int p=1;
	for(int k=30;k>=0;k--)
	{
		int ch=(x>>k)&1;
		if(trie[p][ch]==0)
			trie[p][ch]=++tot;
		p=trie[p][ch];
	}
}
int Trie_search(int x)//搜索 
{
	int p=1,ans=0;
	for(int k=30;k>=0;k--)
	{
		int ch=(x>>k)&1;
		if(trie[p][!ch])//相反的位 
			p=trie[p][!ch],ans+=1<<k;
        else
			p=trie[p][ch];
	}
	return ans;
}
int main()
{
    cin>>n;
    Trie_insert(s[0]);//s[0]也要插入 
    for(int i=1;i<=n;i++)
    {
    	cin>>a;
    	s[i]=s[i-1]^a;
    	Trie_insert(s[i]);
    	mx=max(mx,Trie_search(s[i]));
	}
	cout<<mx<<endl;
	return 0;
}