CF527C Glass Carving

题意

有一块 $w\times h$ 的玻璃，每次横着切一刀 $(H)$ 或者竖着切一刀 $(V)$ ，没有两次相同的切割，求最大的矩形碎片面积。

分析

显然，最大矩形碎片面积 $=$ 最大的长 $\times$ 最大的宽。因为长宽互不干扰，所以我们分开处理。

我们把求长和宽看作查询，把切看成修改，显然我们需要两个支持单点修改+区间查询的线段树。

接下来以 $w$（横着）为例。

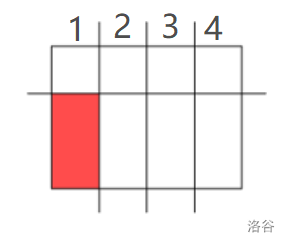
我们线段树中定义的点是一段长度，但题目要把一段长度分开，怎么办呢？

加几个点呗！

没错，由于切割都是整数，所以我们在相邻两个单位长度之间加一个点，原来 $w$ 个点变成了 $2\times w-1$ 个点，第 $x$ 个单位长度与第 $x+1$ 个单位长度之间的间隙相当于第 $2\times x$ 个节点。

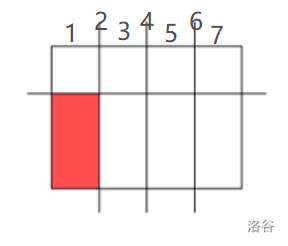
建树时，我们令全局为 $1$。

切断时，我们只要把第 $2\times x$ 个节点改成 $0$，维护最长的连续 $1$ 的个数就行了。

计算答案时，最大矩形碎片面积 $=$（第一个线段树最长的连续 $1$ 的个数 $+1$）$\div2\times$ （第二个线段树最长的连续 $1$ 的个数 $+1$）$\div2$。

友情提示：注意开 long long。

代码

#include<bits/stdc++.h>
#define ll long long
#define pl p<<1
#define pr p<<1|1
using namespace std;
int read(){
	int x=0,f=1;char ch=getchar();
	while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
	while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return x*f;
}
const int N=4e5+10;
int w,h,n,x;
char op;
struct Tree{
	int l,r;
	int lmx,rmx,mx;
}s[2][4*N];
void pushup(int k,int p){
	s[k][p].lmx=s[k][pl].lmx;
	if(s[k][pl].lmx==s[k][pl].r-s[k][pl].l+1)
		s[k][p].lmx=max(s[k][p].lmx,s[k][pl].lmx+s[k][pr].lmx);
	s[k][p].rmx=s[k][pr].rmx;
	if(s[k][pr].rmx==s[k][pr].r-s[k][pr].l+1)
		s[k][p].rmx=max(s[k][p].rmx,s[k][pr].rmx+s[k][pl].rmx);
	s[k][p].mx=max(max(s[k][pl].mx,s[k][pr].mx),max(s[k][p].lmx,s[k][p].rmx));
	s[k][p].mx=max(s[k][p].mx,s[k][pl].rmx+s[k][pr].lmx);
}
void build(int k,int p,int l,int r){
	s[k][p].l=l;s[k][p].r=r;
	if(l==r){
		s[k][p].mx=s[k][p].lmx=s[k][p].rmx=1;
		return;
	}
	int mid=(l+r)>>1;
	build(k,pl,l,mid);
	build(k,pr,mid+1,r);
	pushup(k,p);
}
void change(int k,int p,int x){
	if(s[k][p].l==s[k][p].r){
		s[k][p].mx=s[k][p].lmx=s[k][p].rmx=0;
		return;
	}
	int mid=(s[k][p].l+s[k][p].r)>>1;
	if(x<=mid)
		change(k,pl,x);
	else
		change(k,pr,x);
	pushup(k,p);
}
ll ask(){
	return (ll)(s[0][1].mx+1)/2*(s[1][1].mx+1)/2;
}
int main()
{
    w=read();h=read();n=read();
	build(0,1,1,2*w-1);
	build(1,1,1,2*h-1);
	for(int i=1;i<=n;i++){
		cin>>op;
      x=read();
		if(op=='H')
			change(1,1,2*x);
		else
			change(0,1,2*x);
		cout<<ask()<<endl;
	}
	return 0;
}