P6134 [JSOI2015]最小表示

$\text{Link}$

题意

给定一个有向无环图，节点编号为 $1\sim N$，有 $M$ 条边，你可以删除其中的某些边，使其中任意两点的连通性保持不变（若原图中点 $i$ 到 $j$ 有一条路径，那么新图中 $i$ 到 $j$ 也有一条路径，反之亦然），求最多能删除几条边？

分析

先分析一下样例：

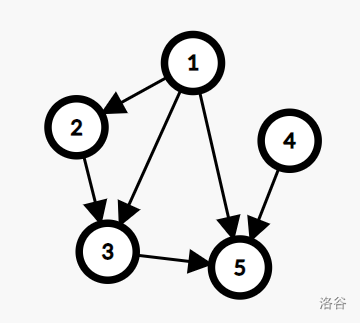
由样例解释得，边 $1\Rightarrow 3$ 和 $1\Rightarrow 5$ 是可以删去的，因为 $1\Rightarrow 3$ 可以用 $1\Rightarrow 2\Rightarrow 3$ 代替；$1\Rightarrow 5$ 可以用 $1\Rightarrow 3\Rightarrow 5$ 代替，进而可以代替为 $1\Rightarrow 2\Rightarrow 3\Rightarrow 5$。

所以，一条边 $i\Rightarrow j$ 可以被删去，仅当存在另一条路径可以替代它，题目中又保证任意两点之间至多只有一条边，所以另一条路径的长度必然大于等于 $2$，即存在一条路径 $i\Rightarrow …\Rightarrow j$，于是问题转化为求 $\sum_{i=1}^n\sum_{j=1}^n[i\Rightarrow j]\land[i\Rightarrow …\Rightarrow j]$。

设边集为 $E$，式子可进一步转化为 $\sum_{e\in E}[e.u\Rightarrow …\Rightarrow e.v]$。

设 $w_{i,j}$ 表示存在一条边 $j\Rightarrow i$，$d_{i,j}$ 表示存在一条路径 $j\Rightarrow …\Rightarrow i$，即这条路径的边数大于等于 $2$，则答案为 $\sum_{e\in E}d_{e.v,e.u}$。

我们对图进行拓补排序，遍历每条边 $x\Rightarrow y$，我们要用 $d_{x,k}$ 和 $w_{x,k}$ 更新 $d_{y,k}$，若 $k$ 到 $x$ 存在边数大于等于 $1$ 的路径，那么经过 $x\Rightarrow y$ 后，就存在边数大于等于 $2$ 的路径了，即 $d_{y,k}=d_{y,k}\lor d_{x,k}\lor w_{x,k}$。

这样做的时间复杂度是 $O(nm)$，$nm$ 最大可能为 $3\times 10^4\times 10^5=3\times10^9$，不能通过此题，不过 $d_{y,k}=d_{y,k}\lor d_{x,k}\lor w_{x,k}$ 部分可以使用 $\text{bitset}$ 优化，复杂度为 $O(\frac{nm}{32})$，可以通过此题。

代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
long long read(){
	long long x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return x*f;
}
void write(long long x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int N=3e4+10;
int n,m,in[N],ans;
vector<int>e[N];
bitset<N>d[N],w[N];
void topu(){
	queue<int>q;
	for(int i=1;i<=n;i++)
		if(!in[i])
			q.push(i);
	while(q.size()){
		int x=q.front();q.pop();
		for(int i=0,y;i<e[x].size();i++){
			in[y=e[x][i]]--;
			d[y]|=d[x]|w[x];
			if(!in[y])
				q.push(y);
		}
	}
}
int main(){
	n=read();m=read();
	for(int i=1,x,y;i<=m;i++){
		x=read();y=read();
		e[x].push_back(y);
		in[y]++;
		w[y][x]=1;
	}
	topu();
	for(int i=1;i<=n;i++)
		for(int j=0;j<e[i].size();j++)
			ans+=d[e[i][j]][i];
	write(ans);
	return 0;
}