P8094 [USACO22JAN] Cow Frisbee S
考场上唯一会的题(wtcl。
题意
一个 的排列 ,求 。
分析
设 ,则满足要求的 最多只有两个: 左边第一个满足 的数和 右边第一个满足 的数。
以下图的 为例:
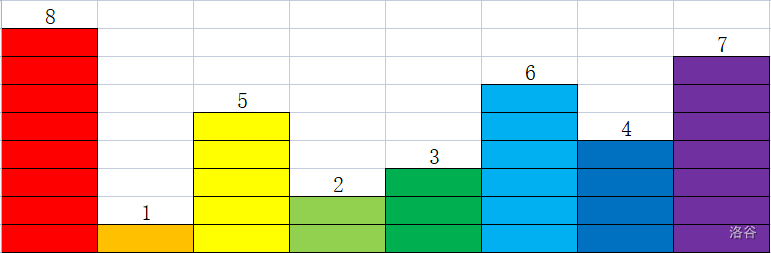
对于 左边的数, 是第一个比它大的,因此中间的数都比他们小,必然满足 。
对于 右边的数, 是第一个比它大的,因此中间的数都比他们小,必然满足 。但是 后面有 ,那么 能不能算入答案呢?显然不能,因为 。
因为 ,所以每个数对 只会从较小的 出发计算的方法计算一次,因此答案不重不漏。
那么如何计算左/右边第一个比 大的数呢,开个小根堆,统计即可,时间复杂度 。
但好像用栈可以 ?管他呢,能过就行。
代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
long long read(){
long long x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void write(long long x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
const int N=3e5+10;
int n,h[N],d[N];
priority_queue<int>q;
ll ans;
int main(){
n=read();
for(int i=1;i<=n;i++){
h[i]=read();
d[h[i]]=i;
while(q.size()&&-q.top()<h[i]){
ans+=abs(i-d[-q.top()])+1;
q.pop();
}
q.push(-h[i]);
}
while(q.size())
q.pop();
for(int i=n;i;i--){
while(q.size()&&-q.top()<h[i]){
ans+=abs(i-d[-q.top()])+1;
q.pop();
}
q.push(-h[i]);
}
write(ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号