《信息学奥赛一本通·高手专项训练》集训 Day 3

矩阵快速幂

$\color{Green}100\color{Black}+\color{Green}100\color{Black}+\color{#5EB95E}95\color{Black}=\color{#5EB95E}295\color{Black}\text{/Rank 6}$

$\color{#FFC116}\text{A. 细胞计算}$

题目

从前有一种细胞，它的增殖方式很奇怪，经过研究，科学家们找到了一个公式来计算其数量：

$$a_n=\begin{cases}xa_{n-1}+n&\text{if }n>1\\1&\text{if }n=1\end{cases}$$

由于这个数字可能非常大，科学家们只打算知道 $a_n\bmod w$ 的值。

题解

构造矩阵 $\begin{bmatrix}a_n&n&1\end{bmatrix}$，构造转移矩阵 $\begin{bmatrix}x&0&0\\1&1&0\\1&1&1\end{bmatrix}$，因此 $\begin{bmatrix}a_n&n&1\end{bmatrix}=\begin{bmatrix}a_1&1&1\end{bmatrix}\times \begin{bmatrix}x&0&0\\1&1&0\\1&1&1\end{bmatrix}^{n-1}$，用矩阵快速幂计算即可。

代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;
long long read() {
    long long x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}
void write(long long x) {
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
const int N = 5;
ll n, x, w;
struct Juz {
    long long a[N][N], h, l;
    void clean() {
        memset(a, 0, sizeof a);
        h = l = 0;
    }
    void build() {
        for (int i = 1; i < N; ++i) a[i][i] = 1;
    }
} p, q;
long long Fmul(long long a, long long b) {
    long long ans = 0;
    while (b) {
        ans = (ans + a * (b & 1)) % w;
        a = (a + a) % w;
        b >>= 1;
    }
    return ans;
}
Juz operator*(const Juz &x, const Juz &y) {
    Juz z;
    z.clean();
    z.h = x.h;
    z.l = y.l;
    for (int i = 1; i <= x.h; ++i)
        for (int j = 1; j <= y.l; ++j)
            for (int k = 1; k <= x.l; ++k) z.a[i][j] = (z.a[i][j] + Fmul(x.a[i][k], y.a[k][j]) % w) % w;
    return z;
}
Juz Juzqmi(Juz a, long long k) {
    Juz ans;
    ans.clean();
    ans.build();
    ans.h = a.h;
    ans.l = a.l;
    while (k) {
        if (k & 1)
            ans = ans * a;
        a = a * a;
        k >>= 1;
    }
    return ans;
}
int main() {
    n = read();
    x = read();
    w = read();
    p.h = 1;
    p.l = 3;
    p.a[1][1] = 1;
    p.a[1][2] = 1;
    p.a[1][3] = 1;
    q.h = 3;
    q.l = 3;
    q.a[1][1] = x;
    q.a[1][2] = 0;
    q.a[1][3] = 0;
    q.a[2][1] = 1;
    q.a[2][2] = 1;
    q.a[2][3] = 0;
    q.a[3][1] = 1;
    q.a[3][2] = 1;
    q.a[3][3] = 1;
    p = p * Juzqmi(q, n - 1);
    write(p.a[1][1]);
    return 0;
}

$\color{#3498DB}\text{B. 数学作业}$

题目

小 C 数学成绩优异，于是老师给小 C 留了一道非常难的数学作业题：

给定正整数 $n,m$，要求计算 $\text{cat}(n) \bmod \ m$ 的值，其中 $\text{cat}(n)$ 是将 $1 \sim n$ 所有正整数 顺序连接起来得到的数。

例如，$n = 13$ , $\text{cat}(n) = 12345678910111213$。小C 想了大半天终于意识到这是一道不可能手算出来的题目，于是他只好向你求助，希望你能编写一个程序帮他解决这个问题。

题解

设正整数 $n$ 的位数为 $k$，则：

$$\text{cat}(n)=10^k\text{cat}(n-1)+n$$

对于不同位数的 $n$，分段使用矩阵快速幂加快递推即可，和第一题类似，先构造矩阵 $\begin{bmatrix}\text{cat}(n)&n&1\end{bmatrix}$，再构造转移矩阵 $\begin{bmatrix}10^k&0&0\\1&1&0\\1&1&1\end{bmatrix}$，所以：

$$\begin{bmatrix}\text{cat}(n)&n&1\end{bmatrix}=\begin{bmatrix}\text{cat}(n-1)&n-1&1\end{bmatrix}\times \begin{bmatrix}10^k&0&0\\1&1&0\\1&1&1\end{bmatrix}$$

矩阵快速幂中的指数应为 $\min\{n,10^k-1\}-10^{k-1}+1$

代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;
ll read() {
    ll x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}
void write(ll x) {
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
const int N = 10;
ll n, m;
int size(ll x) {
    int ans = 0;
    while (x) {
        ans++;
        x /= 10;
    }
    return ans;
}
ll num(int size) {
    ll ans = 1;
    for (int i = 1; i <= size; i++) ans *= 10;
    return ans;
}
struct Juz {
    long long a[N][N], h, l;
    inline void clean() {
        memset(a, 0, sizeof a);
        h = l = 0;
    }
    inline void build() {
        for (int i = 1; i < N; ++i) a[i][i] = 1;
    }
};
Juz operator*(const Juz &x, const Juz &y) {
    Juz z;
    z.clean();
    z.h = x.h;
    z.l = y.l;
    for (int i = 1; i <= x.h; ++i)
        for (int j = 1; j <= y.l; ++j)
            for (int k = 1; k <= x.l; ++k) z.a[i][j] = (z.a[i][j] + x.a[i][k] * y.a[k][j] % m) % m;
    return z;
}
Juz Juzqmi(Juz a, long long k) {
    Juz ans;
    ans.clean();
    ans.build();
    ans.h = a.h;
    ans.l = a.l;
    while (k) {
        if (k & 1)
            ans = ans * a;
        a = a * a;
        k >>= 1;
    }
    return ans;
}
int main() {
    n = read();
    m = read();
    Juz a, b;
    a.h = 1;
    a.l = 3;
    for (int i = 1; i <= 3; i++) a.a[1][i] = 1 % m;
    b.h = b.l = 3;
    b.a[1][1] = 1 % m;
    b.a[1][2] = 0 % m;
    b.a[1][3] = 0 % m;
    b.a[2][1] = 1 % m;
    b.a[2][2] = 1 % m;
    b.a[2][3] = 0 % m;
    b.a[3][1] = 1 % m;
    b.a[3][2] = 1 % m;
    b.a[3][3] = 1 % m;
    int len = size(n);
    for (int i = 1; i < len; i++) {
        b.a[1][1] = num(i) % m;
        a = a * Juzqmi(b, num(i) - num(i - 1) - (i == 1));
    }
    b.a[1][1] = num(len) % m;
    a = a * Juzqmi(b, n - num(len - 1) + 1 - (len == 1));
    cout << a.a[1][1] << endl;
    return 0;
}

$\color{#FFC116}\text{C. 幸运的串}$

A 君喜欢收集特殊的字符串，特别是那些能给他带来幸运的串。

A 君认为一个串是幸运串当且仅当这个串包含长度大于 $1$ 的回文子串。

A 君想知道对于长度恰好为 $n$ 且字符集大小为 $m$ 的所有字符串中（字符集中字符不一定都要用上），有多少个不同的幸运串呢？

最后的结果可能很大，A 君只想知道答案对 $10^9+7$ 取模后的值，请你帮助他。

题解

只有当一个字符串不含长度为 $2$ 或 $3$ 的回文子串时这个字符串才不是幸运串，可以直接推出答案，答案为字符串总个数减去不是幸运串的字符串的个数，即：

$$m^n-m(m-1)(m-2)^{n-2}$$

还有一种矩阵快速幂的解法，设 $f_i$ 表示长度为 $i$ 的幸运字符串的个数，$g_i$ 表示长度为 $i$ 的非幸运串的个数，则有递推式：

$$f_i=\begin{cases}m&i=1\\m^2-m&i=2\\g_{i-1}\times(m-2)&i>2\end{cases}$$ $$g_i=\begin{cases}0&i=1\\m&i=2\\f_{i-1}\times m+g_{i-1}\times2&i>2\end{cases}$$

仍然构造矩阵 $\begin{bmatrix}f_i&g_i\end{bmatrix}$，转移矩阵为 $\begin{bmatrix}m&0\\2&m-2\end{bmatrix}$，计算要用 $\texttt{unsigned long long}$，不然会少 $5$ 分。

代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;
long long read() {
    long long x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}
void write(unsigned long long x) {
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
const int N = 5;
const unsigned ll mod = 1e9 + 7;
unsigned ll n, m;
struct Juz {
    unsigned long long a[N][N], h, l;
    void clean() {
        memset(a, 0, sizeof a);
        h = l = 0;
    }
    void build() {
        for (int i = 1; i < N; ++i) a[i][i] = 1;
    }
    void K_Recursion(int k, int *b) {
        clean();
        h = l = k;
        for (int i = 1; i <= k; i++) a[i][1] = b[i];
        for (int i = 1; i < k; i++) a[i][i + 1] = 1;
    }
} p, q;
unsigned long long Fmul(unsigned long long a, unsigned long long b) {
    unsigned long long ans = 0;
    while (b) {
        ans = (ans + a * (b & 1)) % mod;
        a = (a + a) % mod;
        b >>= 1;
    }
    return ans;
}
Juz operator*(const Juz &x, const Juz &y) {
    Juz z;
    z.clean();
    z.h = x.h;
    z.l = y.l;
    for (int i = 1; i <= x.h; ++i)
        for (int j = 1; j <= y.l; ++j)
            for (int k = 1; k <= x.l; ++k) z.a[i][j] = (z.a[i][j] + Fmul(x.a[i][k], y.a[k][j]) % mod) % mod;
    return z;
}
Juz Juzqmi(Juz a, unsigned long long k) {
    Juz ans;
    ans.clean();
    ans.build();
    ans.h = a.h;
    ans.l = a.l;
    while (k) {
        if (k & 1)
            ans = ans * a;
        a = a * a;
        k >>= 1;
    }
    return ans;
}
int main() {
    n = read();
    m = read();
    if (n == 1) {
        write(0);
        return 0;
    }
    if (n == 2) {
        write(m % mod);
        return 0;
    }
    p.h = 1;
    p.l = 2;
    p.a[1][1] = m % mod;
    p.a[1][2] = (Fmul(m, m) % mod - m % mod + mod) % mod;
    q.h = 2;
    q.l = 2;
    q.a[1][1] = m % mod;
    q.a[1][2] = 0;
    q.a[2][1] = 2;
    q.a[2][2] = (m - 2) % mod;
    p = p * Juzqmi(q, n - 2);
    write(p.a[1][1]);
    return 0;
}

质数与约数

$\color{Green}100\color{Black}+\color{Green}100\color{Black}+\color{Green}100\color{Black}=\color{Green}300\color{Black}/\color{Gold}\text{Rank 1}$

$\color{#FFC116}\text{A. 判断原根}$

题目

在密码系统中，质数扮演了一个很重要的角色。我们对一个称为 $\texttt{Diffie-Hellman}$ 的策划很感兴趣，它可以转换密钥。这种方法需要要一个质数 $p$ 和整数 $r$，并且 $r$ 为 $p$ 的原根。定义：若 $\varphi(p)$ 为最小的 $t$ 满足 $r^t\equiv 1\pmod p$，则 $r$ 为 $p$ 的原根。

由于我们现在想构建一个这样的系统，所以想找出一个原根的一个列表。你的任务是编写一个程序来帮助我们。我们将给定 $p$ 以及一系列的 $r(r<p)$，你需要判断这些 $r$ 是否为 $p$ 的原根。

题解

显然因为 $p$ 是质数，所以 $\varphi(p)=p-1$。

如果学过 $\texttt{BSGS}$，可以想到直接解方程 $r^x\equiv 1\pmod p$ 求出最小的 $x$，判断是否 $x=p-1$ 即可。由于 $\texttt{BSGS}$ 效率太低，所以期望得分 $90$ 分。

接下来考虑正解：若存在一个数 $t$ 使得 $t\neq\varphi(p)$ 且 $r^t\equiv 1\pmod p$，那么显然存在一个循环节 $d$，满足 $r^d\equiv 1\pmod p$，并且 $d|\varphi(p),d|t$，（可能是 $(r^d)^k\equiv 1\pmod p,dk=t$ 或 $dk=\varphi(p)$）。

若存在 $t<\varphi(p)$，那么有 $d\le t<\varphi(p)$，于是问题转化为验证 $d$ 是否存在。设 $q$ 为 $\varphi(p)$ 的一个质因子，若存在 $d|\frac{\varphi(p)}{q}$ 且 $r^d\equiv 1\pmod p$，就有 $r^\frac{\varphi(p)}{q}\equiv 1\pmod p$，因此离线处理出所有的 $q$，得到 $\frac{\varphi(p)}{q}$，用快速幂计算是否满足所有的 $r^\frac{\varphi(p)}{q}\not\equiv 1\pmod p$ 即可。

代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;
ll read() {
    ll x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}
void write(ll x) {
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
const int N = 1e5 + 10;
ll p, n, r, a[N], t;
ll qmi(ll a, ll b) {
    ll ans = 1 % p;
    while (b) {
        if (b & 1)
            ans = ans * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ans;
}
int main() {
    p = read();
    n = read();
    ll q = p - 1;
    for (ll i = 2; i * i <= q; i++) {
        if (q % i == 0) {
            a[++t] = i;
            while (q % i == 0) {
                q /= i;
            }
        }
    }
    if (q != 1)
        a[++t] = q;
    while (n--) {
        r = read();
        if (r % p == 0) {
            puts("NO");
            continue;
        }
        int f = 0;
        for (int i = 1; i <= t; i++) {
            if (qmi(r, (p - 1) / a[i]) % p == 1) {
                f = 1;
                break;
            }
        }
        if (f)
            puts("NO");
        else
            puts("YES");
    }
    return 0;
}

$\color{#FFC116}\text{B. 合并集合}$

题目

你想将 $[a,b]$ 内的所有自然数分成若干个集合。

一开始每个数自己是一个集合，如果某两个数都是一个 $\ge p$ 的素数的倍数，则将这两个数所在的集合合并，问最后有多少个集合。

题解

显然可以用素数不断去枚举倍数筛 $[a,b]$，用并查集把筛到的集合合并。

但素数不一定要筛到 $b$，试想，若存在素数 $q$ 使得 $[a,b]$ 有产生合并的机会，则 $q$ 必然至少有两个倍数落在区间 $[a,b]$，即 $a\le kq\le(k+1)q\le b$，因此 $q\le b-a$，只要筛到 $b-a$ 即可。

代码

#include <bits/stdc++.h>
#define ll long long


using namespace std;
long long read() {
    long long x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}
void write(long long x) {
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
const int N = 2e6 + 10;
ll a, b, p;
ll fa[N], ans;
bool v[N];
void Eratosthenes(ll n) {
    memset(v, 0, sizeof(v));
    for (ll i = 2; i <= n; i++) {
        if (v[i])
            continue;
        for (ll j = i; i * j <= n; j++) v[i * j] = 1;
    }
}
ll get(ll x) { return (fa[x] == x ? x : fa[x] = get(fa[x])); }
int main() {
    a = read();
    b = read();
    p = read();
    Eratosthenes(b - a + 1);
    for (ll i = a; i <= b; i++) fa[i - a] = i - a;
    for (ll i = max(p, (ll)2); i <= b - a + 1; i++) {
        if (v[i])
            continue;
        for (ll j = (a % i ? a / i + 1 : a / i), k = (a % i ? a / i + 1 : a / i); j * i <= b; j++) {
            fa[get(j * i - a)] = get(k * i - a);
        }
    }
    for (ll i = a; i <= b; i++)
        if (get(i - a) == i - a)
            ans++;
    write(ans);
    return 0;
}

$\color{#3498DB}\text{C. 灯光控制}$

题目

学校宿管有一套神奇的控制系统来控制寝室的灯的开关：

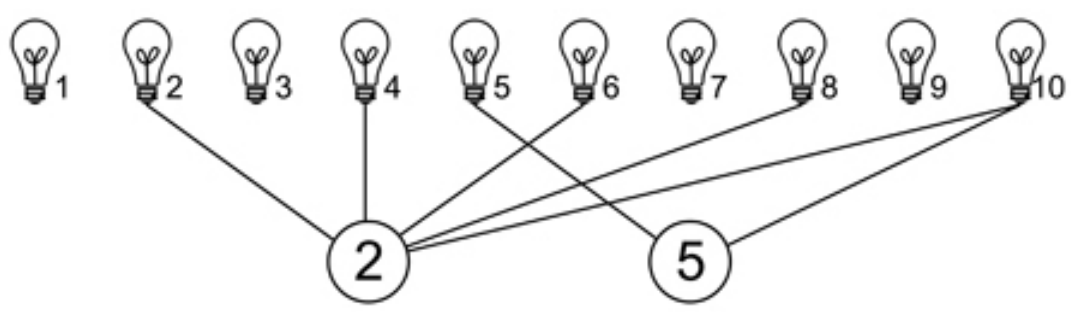
共有 $n$ 盏灯，标号为 $1$ 到 $n$，有 $m$ 个标有不同质数的开关，开关可以控制所有标号为其标号倍数的灯，按一次开关，所有其控制的灭着的灯都点亮，所有其控制的亮着的灯将熄灭。现在，宿管可以无限的按所有开关，所有灯初始状态为熄灭，请求出最多能点亮几盏灯。

题解

显然最优情况下肯定有方案中每个灯至多按一次，再按就没有意义了。

因此可以想到直接暴力去枚举每个灯按或不按，把灯的亮暗情况用 $n$ 位 $\texttt{01}$ 序列来表示，按一次相当于把相关的灯的状态都异或上 $1$，所以每个开关也可以看成一个 $n$ 位 $\texttt{01}$ 操作序列，可以提前预处理，用 $\text{bitset}$ 可以快速维护。

但 $n=1000$ 内的质数有大约 $160$ 个，枚举一定会超时，联想到寿司晚宴这题，我们可以以 $\sqrt n$ 为分界线，把小于和大于 $\sqrt n$ 的质数分开考虑，小于 $\sqrt n$ 的质数最大只有 $11$ 个，可以暴力枚举他们组合的所有情况；大于 $\sqrt n$ 的质数有一个特点，就是选择他只可能被小于 $\sqrt n$ 的质数控制的灯，不会影响其他大于 $\sqrt n$ 的质数控制的灯，因为 $1\sim n$ 中没有同时拥有两个大于 $\sqrt n$ 的质因子的数。

这样，我们就可以在确定小于 $\sqrt n$ 的质数开关情况后，一个个考虑大于 $\sqrt n$ 的质数的情况，如果一个大于 $\sqrt n$ 的质数开关按下后能使亮的灯的个数增多，就贪心地按下它。最后对所有结果取最大值就是答案。

我在代码中为了方便，直接枚举前 $11$ 小的质数开关的方案，效果是一样的。

代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;
long long read() {
    long long x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}
void write(long long x) {
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
const int N = 1010;
int t, n, m, p[N], ans;
bitset<N> e[N];
int main() {
    t = read();
    while (t--) {
        n = read();
        m = read();
        for (int i = 1; i <= m; i++) {
            p[i] = read();
        }
        ans = 0;
        sort(p + 1, p + m + 1);
        for (int i = 1; i <= m; i++) {
            e[i].reset();
            for (int j = 1; j * p[i] <= n; j++) e[i][j * p[i]] = 1;
        }
        bitset<N> s, t;
        for (int i = 0; i < (1 << (min(11, m))); i++) {
            s.reset();
            for (int j = 0; j < min(11, m); j++) {
                if (i & (1 << j))
                    s = s ^ e[j + 1];
            }
            int sum = 0;
            for (int j = min(11, m) + 1; j <= m; j++) {
                t = s ^ e[j];
                if (s.count() < t.count())
                    sum += t.count() - s.count();
            }
            ans = max(ans, sum + (int)s.count());
        }
        write(ans);
        putchar('\n');
    }
    return 0;
}