《信息学奥赛一本通·高手专项训练》集训 Day 4

同余问题

我学到过的知识：$\texttt{Lucas}$ 定理、$\texttt{BSGS}$……

考场涉及的知识：$\texttt{exLucas}$ 定理、$\texttt{exBSGS}$……

我期待的题目：$\text{……保证模数 p 为质数。}$

考场上的题目：$\text{……不保证模数 p 为质数。}$

于是

$\color{Red}0\color{Black}+\color{Yellow}50\color{Black}+\color{Orange}20\color{Black}=\color{Orange}70\color{Black}\text{/Rank 15}$

$\color{#9D3DCF}\text{A.发放奖金}$

题目

老板有 $m$ 元，要给 $n$ 名不同员工发奖金，每名员工的奖金数应当是非负整数，并且 $m$ 元不一定要全部发完。

好奇的老板想知道，给定 $n$ 和 $m$，他有多少种发奖金的方案？这个答案很大，所以再给定一个 $p$，最终的答案取模 $p$ 的余数。

题解

我们增加一个虚拟员工，给他发给其他员工后剩下的钱，然后再增加 $n+1$ 个虚拟币，并要求 $n+1$ 个人包括虚拟员工所有人必须发到钱，这样问题就变成了在 $n+m+1$ 个排成一排的球中间插 $n$ 个木板，使每两块木板之间都不为空有几种方案，显然答案为 $C^n_{n+m}$。

因为模数 $p$ 不是质数，所以我们必须用 $\color{Purple}\texttt{exLucas}$。

代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;
long long read() {
    long long x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}
void write(long long x) {
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
const int N = 15;
ll n, m, p;
ll a[N], b[N];
ll qmi(ll a, ll b, ll p) {
    ll ans = 1 % p;
    while (b) {
        if (b & 1)
            ans = ans * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ans;
}
ll exgcd(ll a, ll b, ll &x, ll &y) {
    if (!b) {
        x = 1;
        y = 0;
        return a;
    }
    ll d = exgcd(b, a % b, x, y);
    ll tmp = x;
    x = y;
    y = tmp - a / b * x;
    return d;
}
ll inv(ll a, ll p_k) {
    ll x, y;
    exgcd(a, p_k, x, y);
    return (x % p_k + p_k) % p_k;
}
ll fac(ll n, ll p, ll p_k) {
    if (!n)
        return 1;
    ll ans = 1;
    for (ll i = 1; i <= p_k; i++)
        if (i % p)
            ans = ans * i % p_k;
    ans = qmi(ans, n / p_k, p_k);
    for (ll i = 1; i <= n % p_k; i++)
        if (i % p)
            ans = ans * i % p_k;
    return ans * fac(n / p, p, p_k) % p_k;
}
ll qC(ll n, ll m, ll p, ll p_k) {
    ll x = 0, y = 0, z = 0;
    for (ll i = p; i <= n; i *= p) x += n / i;
    for (ll i = p; i <= m; i *= p) y += m / i;
    for (ll i = p; i <= (n - m); i *= p) z += (n - m) / i;
    return fac(n, p, p_k) * inv(fac(m, p, p_k), p_k) % p_k * inv(fac(n - m, p, p_k), p_k) % p_k *
           qmi(p, x - y - z, p_k) % p_k;
}
long long CRT(int n, long long *a, long long *m) {
    long long sum = 0, M = 1, x, y;
    for (int i = 1; i <= n; i++) M *= m[i];
    for (int i = 1; i <= n; i++) {
        sum += a[i] * M / m[i] % M * (inv(M / m[i], m[i])) % M;
    }
    return (sum % M + M) % M;
}
ll exlucas(ll n, ll m, ll P) {
    ll tot = 0;
    for (ll p = 2; p * p <= P; p++) {
        if (P % p)
            continue;
        ll p_k = 1;
        while (P % p == 0) {
            p_k *= p;
            P /= p;
        }
        a[++tot] = qC(n, m, p, p_k);
        b[tot] = p_k;
    }
    if (P > 1) {
        a[++tot] = qC(n, m, P, P);
        b[tot] = P;
    }
    return CRT(tot, a, b);
}
int main() {
    n = read();
    m = read();
    p = read();
    write(exlucas(n + m, n, p));
    return 0;
}

$\color{#9D3DCF}\text{B. 经典经典}$

题目

已知数 $a,p,b$，设满足 $a^x\equiv b\pmod p$ 的最小自然数为 $x$。这个问题十分经典，请你求出这个 $x$。

题解

这题就是 $\color{Purple}\texttt{exBSGS}$ 板子，直接套模板即可。

代码

#include <bits/stdc++.h>
#define ll long long


using namespace std;
ll read() {
    ll x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}
void write(ll x) {
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
long long qmi(long long a, long long b, long long c) {
    long long ans = 1;
    while (b) {
        if (b & 1)
            ans = ans * a % c;
        a = a * a % c;
        b >>= 1;
    }
    return ans;
}
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
ll exgcd(ll a, ll b, ll &x, ll &y) {
    if (!b) {
        x = 1;
        y = 0;
        return a;
    }
    ll d = exgcd(b, a % b, x, y);
    ll z = x;
    x = y;
    y = z - a / b * x;
    return d;
}
long long Baby_Step_Giant_Step(long long a, long long b, long long p) {
    map<long long, long long> hash;
    hash.clear();
    b %= p;
    long long t = (long long)sqrt(p) + 1, val;
    for (long long j = 0; j < t; j++) {
        val = (long long)b * qmi(a, j, p) % p;  // b*a^j
        hash[val] = j;
    }
    a = qmi(a, t, p);  // a^t
    if (!a)
        return b ? -1 : 1;
    for (long long i = 0; i <= t; i++) {
        val = qmi(a, i, p);  // (a^t)^i
        long long j = hash.find(val) == hash.end() ? -1 : hash[val];
        if (j >= 0 && i * t - j >= 0)
            return i * t - j;
    }
    return -1;
}
ll exBSGS(ll a, ll b, ll p) {  // a^x=b (mod p)
    a %= p;
    b %= p;
    ll cnt = 0, s = 1, t = 1;
    for (ll i = 0; i <= 50; i++) {
        if (t == b)
            return i;
        t = t * a % p;
    }
    bool f = 0;
    while (1) {
        ll d = gcd(a, p);
        if (d == 1)
            break;
        if (b % d)
            return -1;
        cnt++;
        b /= d;
        p /= d;
        s = s * (a / d) % p;
    }
    ll x, y;
    exgcd(s, p, x, y);
    b = b * (x % p + p) % p;
    ll ans = Baby_Step_Giant_Step(a, b, p);
    if (ans == -1)
        return ans;
    return ans + cnt;
}
int main() {
    ll p, b, n;
    while (cin >> b && b) {
        p = read();
        n = read();
        ll ans = exBSGS(b, n, p);
        if (ans < 0)
            puts("No Solution");
        else
            write(ans), putchar('\n');
    }
    return 0;
}

$\color{#9D3DCF}\text{C. 排列排名}$

题目

给出一个长度为 $N$ 的数列，问该数列在其所有排列中的，按字典序从小到大排列的排名。输出该排名 $\bmod M$ 的值。

注意该数列会有重复元素(而相同元素交换位置依然是同一个排列)，$M$ 不保证为质数。

题解

书上题解的代码似乎是错误的，我仿写了一遍却连样例都过不了，截止到 $\texttt{2022-08-04 23:59}$，通过该题的人都是以非书上题解的方法过的。

如果学过$\color{Green}\texttt{康托展开}$的话，可以发现这题和康托展开类似，只不过元素是可以重复的，我们可以仿照康托展开的思路求解。

求数列的排名相当于求比该排列字典序小的排列的个数 $+1$，我们从左到右逐位考虑，对于第 $i$ 位，只要求前 $i-1$ 位都和原数列一致，从第 $i$ 位开始不同的字典序比原数列下的数列个数即可，显然，若不考虑字典序，此时这个多重集的排列数为 $\frac{(n-i+1)!}{b_1!b_2!…b_k!}$，$b_i$ 表示原序列第 $i\sim n$ 位中元素 $a_i$ 的个数。设 $q(a_i)$ 表示原数列中第 $i$ 位以后比 $a_i$ 小的数的个数，显然只要保证第 $i$ 位填这 $q(a_i)$ 个数之一就能保证字典序小，而第 $i$ 位原来可能为 $n-i+1$ 个数，于是第 $i$ 个位置对答案的贡献为 $\frac{q(a_i)}{n-i+1}\times\frac{(n-i+1)!}{b_1!b_2!…b_k!}=\frac{q(a_i)(n-i)!}{b_1!b_2!…b_k!}$。

设每次枚举的贡献为 $s$，考虑不断维护 $s$。由于阶乘是从大往小增长的，所以我们从大往小枚举 $i$，这样 $(n-i)!$ 可以快速维护，对于 $q(a_i)$，开个树状数组统计即可，分母每次枚举只会变化一个除数，也可以快速计算。

但是，这道题的模数并不是质数，所以我们可以把 $M$ 先质因数分解，对于分子分母中含有的 $M$ 的质因数，直接把质数相减即可，剩下的部分则与 $M$ 互质，直接计算即可。

除法时的逆元怎么求？设求 $c$ 模 $M$ 的乘法逆元，我们已知 $\gcd(c,M)=1$，那么有 $c^{\varphi(M)}\equiv 1\pmod m$，即 $c\times c^{\varphi(M)-1}\equiv 1\pmod m$，即 $c^{\varphi(M)-1}\bmod m$ 就是 $c$ 的乘法逆元，$\varphi(M)$ 可以在分解质因数时求出。

代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;
long long read() {
    long long x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}
void write(long long x) {
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
const int N = 3e5 + 10;
ll n, m, ans = 1, s = 1;
ll pri[N], t, a[N], c[N], mx, tp[N], inv[N];
bool vis[N];
ll qmi(ll a, ll b, ll p) {
    ll ans = 1 % p;
    while (b) {
        if (b & 1)
            ans = (ans * a) % p;
        a = a * a % p;
        b >>= 1;
    }
    return ans;
}
void add(int x, int v) {
    for (; x < N - 5; x += x & -x) c[x] += v;
}
int ask(int x) {
    int ans = 0;
    for (; x; x -= x & -x) ans += c[x];
    return ans;
}
void cheng(ll x) {
    for (int i = 1; i <= t; i++)
        while (x % pri[i] == 0) {
            x /= pri[i];
            tp[i]++;
        }
    s = s * x % m;
}
void chu(ll x) {
    for (int i = 1; i <= t; i++)
        while (x % pri[i] == 0) {
            x /= pri[i];
            tp[i]--;
        }
    s = s * inv[x] % m;
}
ll calc() {
    ll ans = s;
    for (int i = 1; i <= t; i++) ans = ans * qmi(pri[i], tp[i], m) % m;
    return ans;
}
int main() {
    n = read();
    m = read();
    ll nm = m;
    ll ph = m;
    for (int i = 1; i <= n; i++) {
        a[i] = read();
        mx = max(mx, a[i]);
    }
    for (int i = 2; i * i <= nm; i++) {
        if (nm % i == 0) {
            pri[++t] = i;
            ph = ph / i * (i - 1);
            while (nm % i == 0) nm /= i;
        }
    }
    if (nm > 1) {
        pri[++t] = nm;
        ph = ph / nm * (nm - 1);
    }
    add(a[n], 1);
    inv[1] = 1;
    for (int i = n - 1; i; i--) {
        int x = ask(a[i] - 1);
        add(a[i], 1);
        cheng(n - i);
        inv[n - i + 1] = qmi(n - i + 1, ph - 1, m);
        chu(ask(a[i]) - x);
        if (!x)
            continue;
        cheng(x);
        ans = (ans + calc()) % m;
        chu(x);
    }
    write(ans);
    return 0;
}

组合数学

$\color{Green}100\color{Black}+\color{Red}0\color{Black}+\color{Red}0\color{Black}=\color{Orange}100\color{Black}\text{/Rank 19}$

$\color{#9D3DCF}\text{A. 组合取模}$

题目

给定 $n,m,p$，求 $C_n^m\bmod p$。

题解

这题就是 $\color{Purple}\texttt{exLucas}$ 板子，直接套模板即可。

代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;
long long read() {
    long long x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}
void write(long long x) {
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
const int N = 15;
ll n, m, p;
ll a[N], b[N];
ll qmi(ll a, ll b, ll p) {
    ll ans = 1 % p;
    while (b) {
        if (b & 1)
            ans = ans * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ans;
}
ll exgcd(ll a, ll b, ll &x, ll &y) {
    if (!b) {
        x = 1;
        y = 0;
        return a;
    }
    ll d = exgcd(b, a % b, x, y);
    ll tmp = x;
    x = y;
    y = tmp - a / b * x;
    return d;
}
ll inv(ll a, ll p_k) {
    ll x, y;
    exgcd(a, p_k, x, y);
    return (x % p_k + p_k) % p_k;
}
ll fac(ll n, ll p, ll p_k) {
    if (!n)
        return 1;
    ll ans = 1;
    for (ll i = 1; i <= p_k; i++)
        if (i % p)
            ans = ans * i % p_k;
    ans = qmi(ans, n / p_k, p_k);
    for (ll i = 1; i <= n % p_k; i++)
        if (i % p)
            ans = ans * i % p_k;
    return ans * fac(n / p, p, p_k) % p_k;
}
ll qC(ll n, ll m, ll p, ll p_k) {
    ll x = 0, y = 0, z = 0;
    for (ll i = p; i <= n; i *= p) x += n / i;
    for (ll i = p; i <= m; i *= p) y += m / i;
    for (ll i = p; i <= (n - m); i *= p) z += (n - m) / i;
    return fac(n, p, p_k) * inv(fac(m, p, p_k), p_k) % p_k * inv(fac(n - m, p, p_k), p_k) % p_k *
           qmi(p, x - y - z, p_k) % p_k;
}
long long CRT(int n, long long *a, long long *m) {
    long long sum = 0, M = 1, x, y;
    for (int i = 1; i <= n; i++) M *= m[i];
    for (int i = 1; i <= n; i++) {
        sum += a[i] * M / m[i] % M * (inv(M / m[i], m[i])) % M;
    }
    return (sum % M + M) % M;
}
ll exlucas(ll n, ll m, ll P) {
    ll tot = 0;
    for (ll p = 2; p * p <= P; p++) {
        if (P % p)
            continue;
        ll p_k = 1;
        while (P % p == 0) {
            p_k *= p;
            P /= p;
        }
        a[++tot] = qC(n, m, p, p_k);
        b[tot] = p_k;
    }
    if (P > 1) {
        a[++tot] = qC(n, m, P, P);
        b[tot] = P;
    }
    return CRT(tot, a, b);
}
int main() {
    n = read();
    m = read();
    p = read();
    write(exlucas(n, m, p));
    return 0;
}

$\color{#52C41A}\text{B. 数列方案}$

题目

求有多少种不同的长度为 $n$ 的整数数列 $A$，满足 $0\le A_1\le A_2\le……\le A_n\le m$。 由于答案较大，你只需要输出答案的最后 $100$ 位，如果这个值不足 $100$ 位，请在空位上补 $0$。

题解

有重复的数列 $A$ 不好算，我们可以设 $B_i=A_i+i$，则问题可以等价地转化为：求有多少种不同的长度为 $n$ 的整数数列 $B$，满足 $1\le B_1<B_2<……< B_n\le m+n$。显然答案为 $C_{n+m}^n$，直接高精计算即可。

代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;
long long read() {
    long long x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}
void write(long long x) {
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
const int N = 5e4 + 10, L = 110;
int n, m, tot, b[N], pri[N];
bool check[N];
ll ans;
struct bignum {
    int len, a[L];
    bignum() {
        len = 1;
        memset(a, 0, sizeof(a));
    }
    bignum operator*(const bignum &b) {
        bignum c;
        for (int i = 1; i <= len; i++)
            for (int j = 1; j <= b.len; j++) {
                if (i + j > 101)
                    break;
                c.a[i + j - 1] += a[i] * b.a[j];
                c.a[i + j] += c.a[i + j - 1] / 10;
                c.a[i + j - 1] %= 10;
            }
        c.len = min(100, len + b.len);
        while (c.len > 1 && c.a[c.len] == 0) c.len--;
        return c;
    }
    void print() {
        for (int i = 100; i; i--) write(a[i]);
        puts("");
    }
} Ans;
bignum qmi(int num, int exp) {
    bignum res, x;
    res.a[1] = res.len = 1;
    x.len = 0;
    while (num) {
        x.a[++x.len] = num % 10;
        num /= 10;
    }
    if (!x.len)
        x.len = 1;
    while (exp) {
        if (exp & 1)
            res = res * x;
        x = x * x;
        exp >>= 1;
    }
    return res;
}
void dic(int x, int y) {
    int tmp;
    for (int i = 1; i <= tot; i++) {
        tmp = pri[i];
        while (x % tmp == 0) {
            b[i] += y;
            x /= tmp;
        }
        if (x == 1)
            break;
    }
    return;
}
void prime() {
    check[0] = check[1] = 1;
    for (int i = 2; i < N; i++) {
        if (!check[i])
            pri[++tot] = i;
        for (int j = 1; j <= tot; j++) {
            if (i * pri[j] >= N)
                break;
            check[i * pri[j]] = 1;
            if (i % pri[j] == 0)
                break;
        }
    }
}
int main() {
    n = read();
    m = read();
    if (n < m)
        swap(n, m);
    if (n <= 10 && m <= 10) {
        ans = 1;
        int nm = n + m;
        for (int i = 1; i <= nm; i++) ans *= i;
        for (int i = 1; i <= n; i++) ans /= i;
        for (int i = 1; i <= m; i++) ans /= i;
        printf("%0100lld\n", ans);
        return 0;
    }
    prime();
    for (int i = n + m; i > n; i--) dic(i, 1);
    for (int i = 2; i <= m; i++) dic(i, -1);
    Ans.a[1] = 1;
    for (int i = 1; i <= tot; i++)
        if (b[i])
            Ans = Ans * qmi(pri[i], b[i]);
    Ans.print();
    return 0;
}

$\color{#9D3DCF}\text{C. 宇宙蘑菇}$

题目

你发现了一种奇怪的蘑菇，它每天都会固定分裂一次，长度为 $x$ 的蘑菇会分裂成两个长度分别为 $x-1$ 和 $x+1$ 的蘑菇，但是长度为 $0$ 的蘑菇是不存在的，所以长度为 $1$ 的蘑菇只能生长成长度为 $2$ 的蘑菇。

现在你第一天有一个长度为 $2$ 的蘑菇，你想知道第 $n$ 天有多少个蘑菇。

题解

设 $f_{i,j}$ 表示第 $i$ 天长度为 $j$ 的蘑菇的个数，如果把它当做平面上的点 $(i,j)$，不考虑不经过 $x$ 轴的限制，则 $f_{i,j}$ 表示从 $(1,2)$ 出发，每次可以向右上或右下走 $\sqrt2$ 个单位长度，走到 $(i,j)$ 的方案数，答案为 $C_{i-1}^{\frac{i-j+1}{2}}$。

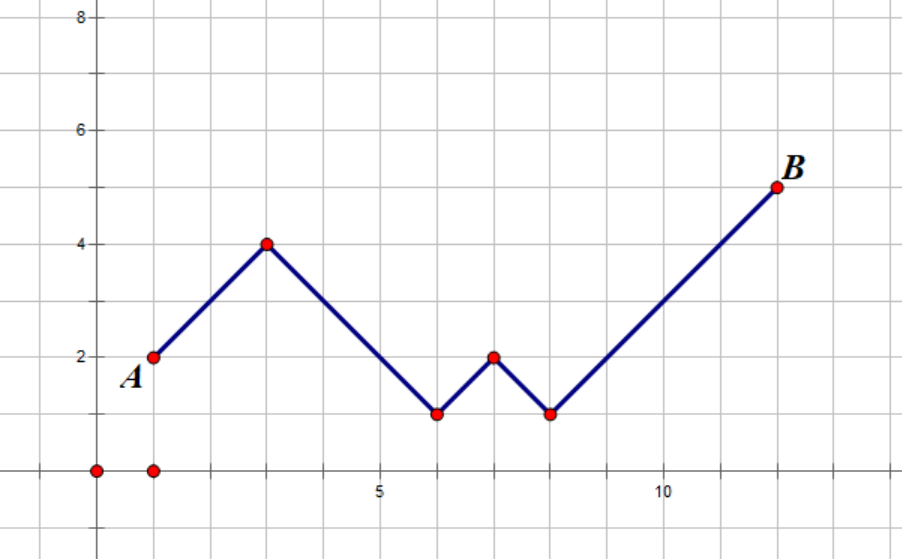
若加上限制，则有部分路径经过 $x$ 轴，是不符合要求的，我们可以把它与 $x$ 轴第一个交点之间的路径以 $x$ 轴为轴翻折，得到一个等价的路径，从总数中减去这部分路径的个数即可，个数为 $C_{i-1}^{\frac{i-j-3}{2}}$。

所以答案为：

$$ans=\sum_{i=1}^{n+1}f_{n,i}=\sum_{i=1}^{n+1}(C_{n-1}^{\frac{n-i+1}{2}}-C_{n-1}^{\frac{n-i-3}{2}})=\sum_{i=1}^{\left\lfloor\frac{n}{2}\right\rfloor}C_{n-1}^{i}-\sum_{i=-2}^{\left\lfloor\frac{n}{2}\right\rfloor-2}C_{n-1}^{i}=C_n^{\left\lfloor\frac{n}{2}\right\rfloor}$$

用高精度计算即可。

代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;
long long read() {
    long long x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}
void write(long long x) {
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
const int N = 5e4 + 10, mod = 1e6;
int n;
struct bignum {
    ll len, a[N];
    bignum() {
        len = 1;
        memset(a, 0, sizeof(a));
    }
    friend bignum operator*(bignum a, int b) {
        bignum res;
        res.len = a.len;
        for (int i = 1; i <= a.len; i++) {
            res.a[i + 1] = (a.a[i] * b + res.a[i]) / mod;
            res.a[i] = (a.a[i] * b + res.a[i]) % mod;
        }
        if (res.a[res.len + 1])
            res.len++;
        return res;
    }
    friend bignum operator/(bignum a, int b) {
        bignum res;
        res.len = a.len;
        for (int i = a.len; i >= 1; i--) {
            res.a[i] = a.a[i] / b;
            a.a[i - 1] += a.a[i] % b * mod;
        }
        while (res.len > 1 && !res.a[res.len]) res.len--;
        return res;
    }
} ans;
int main() {
    n = read();
    ans.a[1] = 1;
    for (int i = (n >> 1) + 1; i <= n; i++) ans = ans * i;
    for (int i = 1; i <= n - (n >> 1); i++) ans = ans / i;
    for (int i = ans.len; i; i--) {
        if (i == ans.len)
            printf("%d", ans.a[i]);
        else
            printf("%06d", ans.a[i]);
    }
    return 0;
}