信友队集训 D2T2 简单图

Problem ID: 4305 D2T2 简单图

题意

给出一个 $n$ 个点 $m$ 条边的仙人掌，即任意一个点至多只存在于一个简单环中的图。

计算对于每一个点，假如我们选某一棵最优的生成树，使得它在生成树上到任意一个点的最远距离最近，对于每个点输出这个距离。

数据范围： $1 \le n,m\le 5\times 10^5$

众所周知除D5T2外其他T2都是最难的

思路

样例的仙人掌大概长这样：

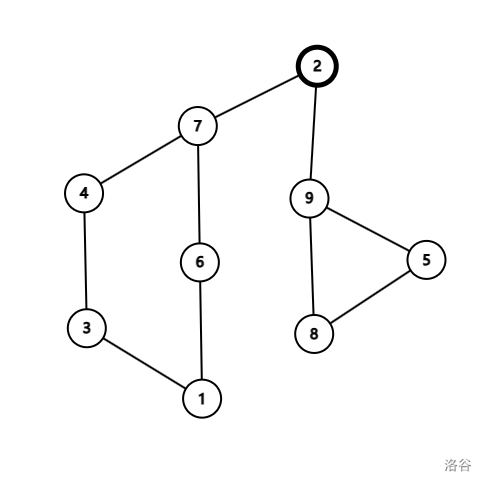
先考虑对于每个点怎样选出最优的一颗生成树，使它在生成树上到任意一个点的最远距离最近。

以 $2$ 号点为例，我们可以先把 $2$ 号点作为这个图的根，把环看成一个点，这样的话这个图就会变成一个树（仙人掌的性质），环与不在环上的点间的边一定在最优的生成树上，不然生成树就会不连通了，因此，决定生成树是否最优的是环上的边，我们要在每个环上删去一条边，使根节点到环上各点的距离最小，同时也保证了环上节点的子节点到根节点的距离也最小。

我们定义遍历时遍历到的第一个环上的点为入点，如图中的入点为 $7,9$ ，显然该删去的边就是在环上离入点最远的边，这样就可以保证环上的点到入点的距离都是环上较小的一段，如入点 $7$ 所在的环中应删去的边是 $3 \leftrightarrow 1$ 。

如果我们选的根节点为在环上的点，只要把根节点当入点处理就可以了。

---

知道最优生成树怎么来后，我们考虑如何计算这个最远的距离。

一段距离对应着以所求节点为端点的链，对于每个点，我们可以维护几个信息：

• $\texttt{down[i]}:$ 从节点 $i$ 往它的子节点走能达到的最远的距离。
• $\texttt{up[i]}:$ 从节点 $i$ 往它的子节点以外的方向（根节点、环上的其他点）走能达到的最远的距离。
• $\texttt{rdown[i]}:$ 从入点 $i$ 往它的子节点走和往环上的其他点走能达到的最远的距离。

显然有：

$$down_u=\max_{v\in son(u)}{rdown_v+1}$$ $$rdown_u=\max_{v\in dcc(u)}{down_v+\min(len(u,v),len(v,u))}$$ $$up_u=\max_{v\in dcc(u)\land u\neq v}{len(v,u)+down_v}$$

如果 $u$ 为入点还应该加上：

$$up_u=\max_{v\in dcc(u)\land u\neq v}{len(v,u)+down_v}$$

如果 $u$ 为入点还应该加上：

$$rdown_u=\max_{v\in dcc(u)}{down_v+\min(len(u,v),len(v,u))}$$ $$up_u=\max\{up_{fa_u}+1,\max_{v\in son(fa_u)\land v\neq u}{rdown_v+2}\}$$

---

接下来维护这些信息的步骤就很清晰了：

1. 建图。可以把仙人掌建成一个圆方树，将每个连通分量上的点都存在代表连通分量的 $\texttt{vector}$ 里，并标记入点，记录每个点所在的连通分量。
2. 然后进行一次遍历，自底向上更新信息 $down_u$ 和 $rdown_u$ ，同时更新 $up_u=\max_{v\in son(fa_u)\land v\neq u}{rdown_v+2}$ ，为了保证存的最大值满足 $u$ 不等于 $v$ ，还应该维护一个次大值使最大值也能找到对应的 $\max$ 。
3. 最后再进行一次遍历，自上而下更新信息 $up_u$ 剩下的部分，由于此时所求点已经转移到了连通分量内，所以入点 $u$ 的父节点也会成为其子节点， $down_u$ 还要被 $up_u$ 更新。更新 $up_u$ 时可以破环为链，用单调队列维护前面节点对应的转移的最大值，顺时针和逆时针各来一次，这样前后都能转移过来，注意任何时候 $len(u,v)$ 都不能大于环长的一半。

---

显然节点 $u$ 答案为 $\max\{up_u,down_u\}$ 。

代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
long long read(){
	long long x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return x*f;
}
void write(long long x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int N=5e5+10;
int n,m,cnt;
int down[N],up[N],rdown[N],fa[N],c[N],q[N<<1];
bool vis[N],ru[N];
vector<int>e1[N],dcc[N],e3[N];
void dfs1(int x){
	vis[x]=1;
	for(int i=0;i<e1[x].size();i++){
		int y=e1[x][i];
		if(!vis[y]){
			e1[y].erase(find(e1[y].begin(),e1[y].end(),x));
			fa[y]=x;
			dfs1(y);
		}
		else if(!c[y]){
			ru[y]=1;
			c[y]=++cnt;
			dcc[cnt].push_back(y);
			for(int j=x;j!=y;j=fa[j]){
				c[j]=cnt;
				dcc[cnt].push_back(j);
			}
		}
	}
	if(!c[x]){
		c[x]=++cnt;
		ru[x]=1;
		dcc[cnt].push_back(x);
	}
}
void calc1(int x){
	for(int i=0;i<dcc[c[x]].size();i++){
		int y=dcc[c[x]][i];
		int fi=0,se=-1e9;
		for(int j=0;j<e1[y].size();j++){
			int z=e1[y][j];
			if(c[y]==c[z])
				continue;
			if(down[z]+1>=fi){
				se=fi;
				fi=rdown[z]+1;
			}
			else if(down[z]+1>se)
				se=rdown[z]+1;
		}
		down[y]=max(down[y],fi);
		rdown[x]=max(rdown[x],fi+min(i,(int)dcc[c[x]].size()-i));
		for(int j=0;j<e1[y].size();j++){
			int z=e1[y][j];
			if(c[y]==c[z])
				continue;
			up[z]=max(up[z],rdown[z]+1==fi?se+1:fi+1);
		}
	}
}
void dfs2(int x){
	vis[x]=1;
	for(int i=0;i<e1[x].size();i++){
		int y=e1[x][i];
		if(!vis[y])
			dfs2(y);
	}
	if(ru[x])
		calc1(x);
}
void calc2(int x){
	down[x]=max(down[x],up[x]);
	for(int i=0;i<2;i++)
		for(int j=0;j<dcc[c[x]].size();j++)
			e3[c[x]].push_back(dcc[c[x]][j]);
	int l=1,r=0;
	for(int i=0;i<e3[c[x]].size();i++){
		if(l<=r&&(i-q[l])*2>dcc[c[x]].size())
			l++;
		if(l<=r)
			up[e3[c[x]][i]]=max(up[e3[c[x]][i]],i-q[l]+down[e3[c[x]][q[l]]]);
		while(l<=r&&-q[r]+down[e3[c[x]][q[r]]]<-i+down[e3[c[x]][i]])
			r--;
		q[++r]=i;
	}
	l=1,r=0;
	for(int i=e3[c[x]].size()-1;i>=0;i--){
		if(l<=r&&(q[l]-i)*2>dcc[c[x]].size())
			l++;
		if(l<=r)
			up[e3[c[x]][i]]=max(up[e3[c[x]][i]],q[l]-i+down[e3[c[x]][q[l]]]);
		while(l<=r&&q[r]+down[e3[c[x]][q[r]]]<i+down[e3[c[x]][i]])
			r--;
		q[++r]=i;
	}
	for(int i=0;i<dcc[c[x]].size();i++){
		int y=dcc[c[x]][i];
		for(int j=0;j<e1[y].size();j++){
			int z=e1[y][j];
			if(c[y]==c[z])
				continue;
			up[z]=max(up[z],up[y]+1);
		}
	}
}
void dfs3(int x){
	vis[x]=1;
	if(ru[x])
		calc2(x);
	for(int i=0;i<e1[x].size();i++){
		int y=e1[x][i];
		if(!vis[y])
			dfs3(y);
	}
}
int main(){
	n=read();m=read();
	for(int i=1;i<=m;i++){
		int u,v;
		u=read();v=read();
		e1[u].push_back(v);
		e1[v].push_back(u);
	}
	dfs1(1);
	memset(vis,0,sizeof(vis));
	dfs2(1);
	memset(vis,0,sizeof(vis));
	dfs3(1);
	for(int i=1;i<=n;i++){
		write(max(down[i],up[i]));
		puts("");
	}
	return 0;
}

双倍经验

P4244 [SHOI2008] 仙人掌图 II 虽然仙人掌定义都不一样