1月做题记录

1.2

$\color{Purple}\text{ CF833D Red-Black Cobweb\ \ \ \ \ }\color{Green}\text{No FST}$

直接考虑淀粉质，设黑点数为 $x$，白点数为 $y$，两条路径拼接起来符合题意的充要条件是 $\dfrac{1}{2}\le \dfrac{x_1+x_2}{y_1+y_2}\le2$，即 $x_1-2y_1\le2y_2-x_2$ 且 $y_2-2x_2\le2x_1-y_1$，可以转化为二维数点解决，但这样使用 $\text{CDQ}$ 分治复杂度有点高，令所有路径乘积为 $mul$，符合条件 $1$ 的乘积为 $mul_1$，符合条件 $2$ 的为 $mul_2$，那么 $\dfrac{mul1\times mul2}{mul}$ 也是答案，直接用树状数组维护即可。

$\color{Purple}\text{ P4886 快递员\ \ \ \ \ }\color{Red}\text{FST=15}$

可以发现，随便取一点 $t$ 计算答案，记此时距离最长的快递路线的集合为 $S$。

• 若存在 $(u\rightarrow v)\in S$，$u,v$位于 $t$ 的两个不同的子树内，那么换成其他点后答案不可能更优，$t$ 点就是答案点。
• 若存在 $(u_1\rightarrow v_1)\in S,(u_2\rightarrow v_2)\in S$，$(u_1\rightarrow v_1),(u_2\rightarrow v_2)$位于 $t$ 的两个不同的子树内，那么换成其他点后答案不可能更优，$t$ 点就是答案点。
• 否则，所有 $S$ 中的快递路线都在同一个子树内，此时答案点可能就在该子树中。

使用淀粉质求解即可。

$\color{Blue}\text{ P8907 [USACO22DEC] Making Friends P\ \ \ \ \ }\color{Red}\text{FST=1}$

删掉一个点时，显然将它的连边信息都连接到其所连的编号最小的点不会影响后面的操作，删点时统计一下总朋友数，再减去一开始的，就是答案。

合并就直接上启发式合并。

1.3

$\color{Purple}\text{P3266 [JLOI2015] 骗我呢\ \ \ \ \ }\color{Green}\text{No FST}$

同一行的数是单调递增的，而数只有 $m+1$ 种，所以每一行都会少一个数 $x$，不妨以此作为状态。

设 $f_{i,j}$ 表示第 $i$ 行缺少数字 $j$ 的方案数，设第 $i-1$ 行缺少 $k$，若 $j+1<k$，那么有 $a_{i,j+1}=j+1=a_{i-1,j+2}$，不合题意，所以 $k\le j+1$，故 $f_{i,j}=\sum_{k=0}^{j+1}f_{i-1,j}=f_{i,j-1}+f_{i-1,j+1}$，放在坐标系里就变成了：

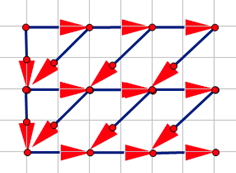
进一步转化：

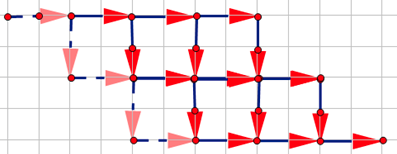
为了方便看，再对称一下：

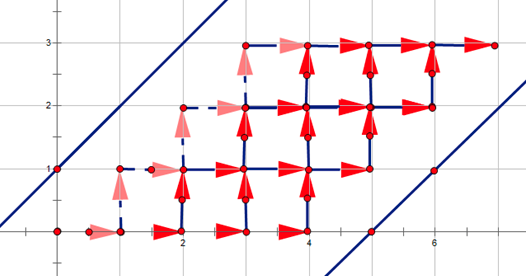
不难发现这就是从 $(0,0)$ 到 $(n+m+1,n)$ 不经过 $A:y=x+1$ 与 $B:y=x-(m+2)$ 的路径条数，需要容斥，一条不合法方案肯定会经过 $AABBBABAA$ 这种路径，压缩一下就是 $ABABA$，考虑翻折，分别求出结尾是 $A,B,AB,BA,ABA,BAB...$ 的方案数再根据奇偶性加减即可。

$\color{Black}\text{ CF1344E Train Tracks\ \ \ \ \ }\color{Green}\text{No FST}$

一次转换的进行的时刻肯定是在上一次是走不同儿子的火车开过的时刻 $l$ 之后，下一车要开过的时刻 $r$ 之前，即 $t\in (l,r]$，不妨求出所有的区间，就能将本题转化为简单的贪心。

假设求出了每个子节点的区间，那么只需将其合并到父节点即可，可以直接采用启发式合并 $+\text{set}$，可以证明最终的区间个数与启发式合并复杂度同阶。

1.4

$\color{Purple}\text{P3349 [ZJOI2016] 小星星\ \ \ \ \ }\color{Green}\text{No FST}$

设 $f_{i,j,s}$ 表示以 $i$ 为根的子树的点在图中的编号集合为 $s$，点 $i$ 编号为 $j$ 的方案数，转移方程是平凡的，但时间爆炸。

注意到 $n$ 很小，可以改变状态表示，枚举集合 $s$，设 $f_{i,j}$ 表示以 $i$ 为根的子树的节点编号都来自 $s$，点 $i$ 编号为 $j$ 的方案数，也就是编号可重复，再进行容斥就是答案。

1.8

$\color{Purple}\text{ CF1009F Dominant Indices\ \ \ \ \ }\color{Green}\text{No FST}$

转移方程显然有：

$$f_{u,dep}=[dep=0]+\sum_{v\in son(u)}f_{v,dep-1}$$

发现第二维只和深度有关，考虑使用长链剖分优化，对于 $u$ 来说，先让他直接从重儿子转移，可以直接令数组下标 $f_u=f_v-1$，轻儿子直接暴力合并即可，这样总复杂度为 $O(n)$。

1.9

$\color{Blue}\text{ CF1919D 01 Tree\ \ \ \ \ }\color{Green}\text{No FST}$

一开始以为树的形态是传统意义上的，想了个有意思的解法，然后发现题目看错了（反正我也没打这场

观察题目，发现唯一能确定的路线是 $a_i=0$ 的，一路上必定都是 $0$，若存在多个这样的 $a_i$ 或没有则无解。

将这条路径从树上移除后，原树会分裂为若干棵子树，其向路径的连边都是 $1$，于是可以把整个区间 $-1$ 再递归去做即可。

$\color{Purple}\text{ P3565 [POI2014] HOT-Hotels\ \ P5904 加强版\ \ \ \ \ }\color{Green}\text{No FST}$

满足要求的图像可能是以下几种形态：

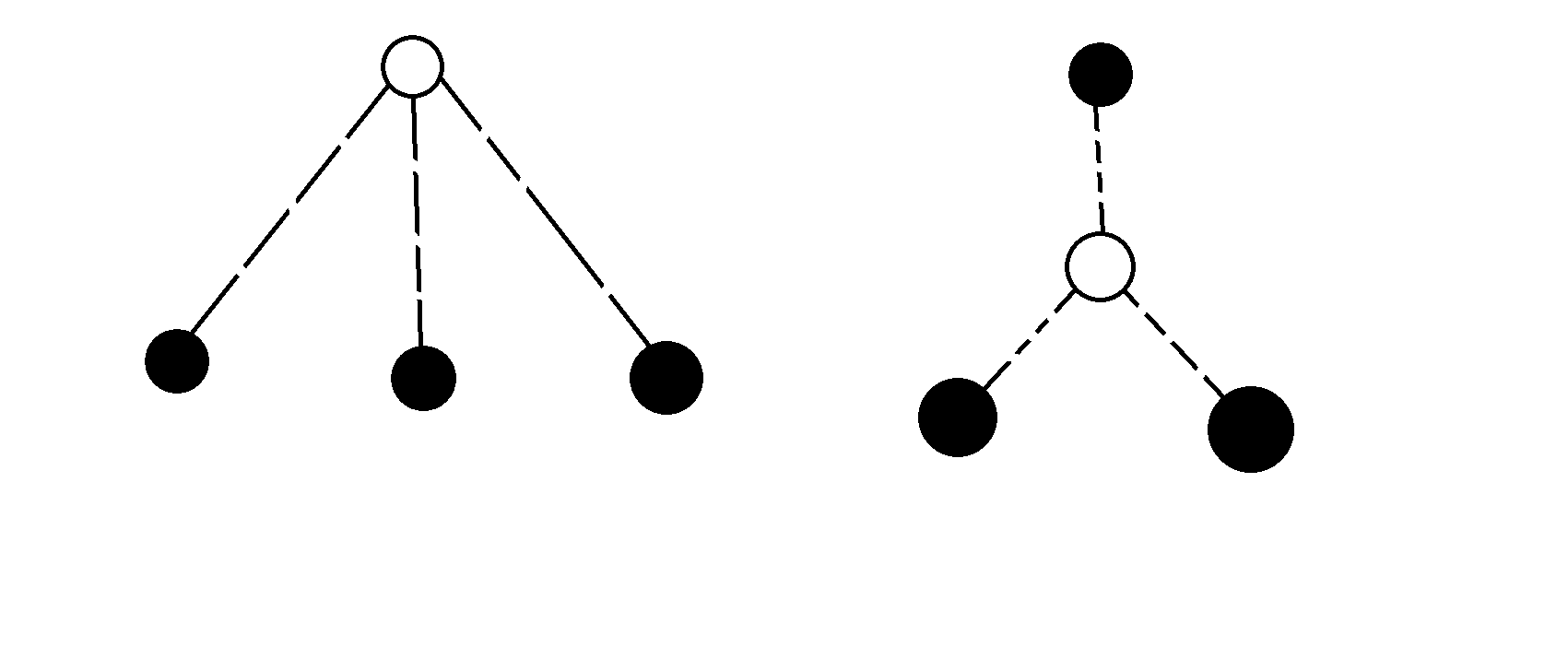
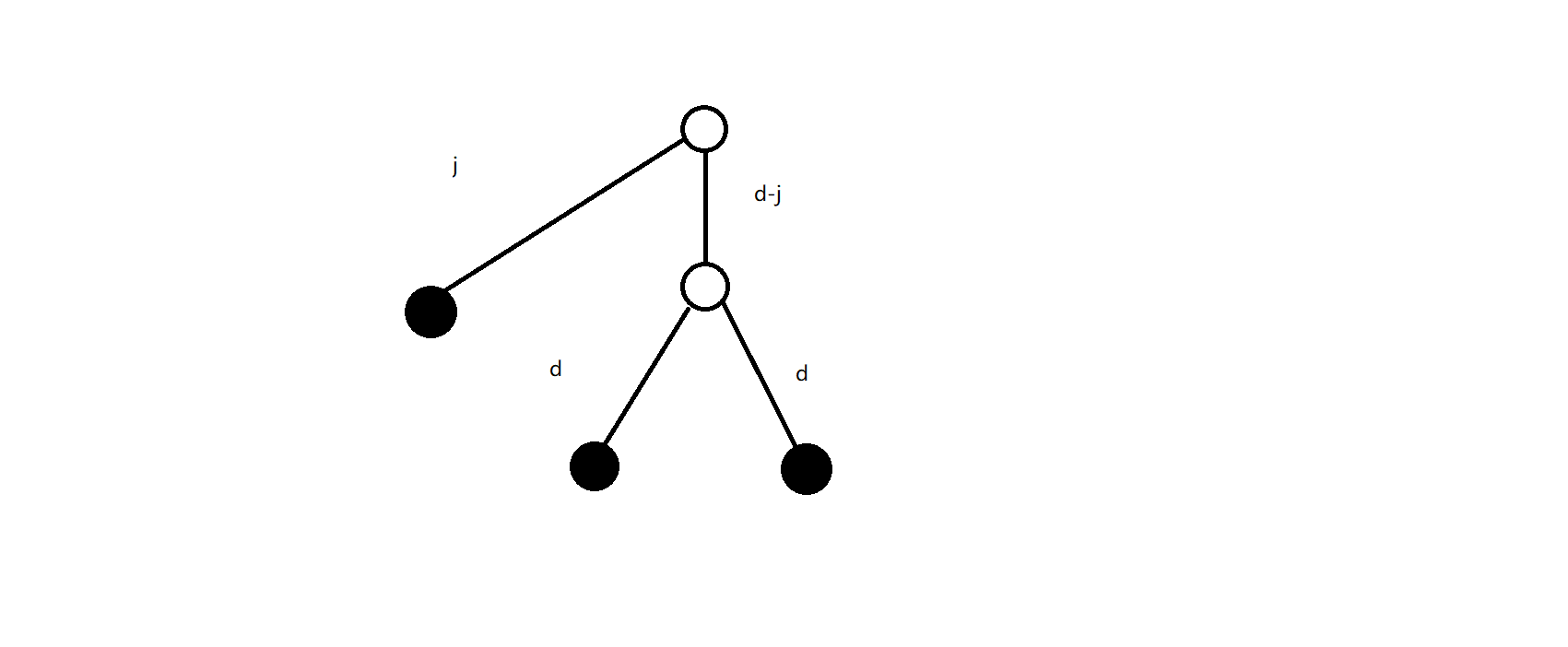
先用一个$\color{Purple}\text{ CF1009F Dominant Indices}$ 的 $f$ 数组，不难发现上面几种形态都可以表示为 $f$ 与第二种形态的组合，于是令 $g_{i,j}$ 表示 $i$ 的子树内满足 $dist(x,\text{lca}(x,y))=dist(y,\text{lca}(x,y))=dist(i,\text{lca}(x,y))+j$ 的方案数，于是有：

$$ans\leftarrow\sum_{i=1}^n(g_{i,0}+\sum_{x,y\in son(i),x\neq y}f_{x,j-1}\times g_{y,j+1})$$ $$g_{i,j}\leftarrow \sum_{x\in son(i)}g_{x,j+1}+\sum_{x,y\in son(i),x\neq y}f_{x,j-1}\times f_{y,j-1}$$ $$f_{i,j}\leftarrow \sum_{x\in son(i)}f_{x,j-1}$$

依然使用长链剖分优化即可，注意 $g$ 数组可能往前占用空间，所以要开双倍。

1.10

$\color{Purple}\text{ P1231 教辅的组成\ P2891 [USACO07OPEN] Dining G\ P1402 酒店之王\ \ \ \ \ }\color{Red}\text{FST=3}$

网络流建模题。

考虑源点向练习连流量为 $1$ 的边，汇点向答案连流量为 $1$ 的边，限制其使用次数，再根据题目给出的条件由练习和答案向书连边，但这样一本书可能会用多次，于是考虑拆点，在书 $a$ 与 $a'$ 间 连流量为 $1$ 的边，限制其使用次数。

$\color{Purple}\text{ P2598 [ZJOI2009] 狼和羊的故事\ \ \ \ \ }\color{Red}\text{FST=1}$

源点和汇点分别向羊和狼连流量为 $inf$ 的边，相邻格子间连流量为 $1$ 的边，求最小割即可。

$\color{Purple}\text{ P2472 [SCOI2007] 蜥蜴\ \ \ \ \ }\color{Green}\text{No FST}$

与 $\color{Purple}\text{ P2598 [ZJOI2009] 狼和羊的故事}$ 类似。

1.11

$\color{Purple}\text{ P2774 方格取数问题\ \ \ \ \ }\color{Green}\text{No FST}$

将格子当作点，向四周连流量为 $inf$ 的边，保证相邻格子捆绑在一起，然后将黑白染色后的点分别向源汇点连流量为点权的边，求出最小割即可。

$\color{Purple}\text{ P4001 [ICPC-Beijing 2006] 狼抓兔子\ \ \ \ \ }\color{Red}\text{FST=7}$

一眼最小割板子，然后发现复杂度爆炸，考虑正解。

给出的图是一个平面图，所以割开的边一定可以构成从左下角到右上角的相邻边路径，跑最短路即可。

然而我还是最小割+面向数据编程水过的。

1.12

$\color{Purple}\text{ P2766 最长不下降子序列问题\ \ \ \ \ }\color{Red}\text{FST=3}$

对于第一问，直接 $\text{dp}$ 即可。

对于第二问，要保证走的一定是最长路，只需保留在最长路上的边即可，即 $f_u=f_v+1$。

对于第三问，瞎改一下 $1,n$ 的流量即可。

$\color{Purple}\text{ P1646 [国家集训队] happiness\ \ \ \ \ }\color{Red}\text{FST=3}$

如果不考虑同选，那么直接向源/汇点连文/理的贡献跑最小割即可。

对于多个点同时选择的情况，考虑建立一个虚点，虚点向源/汇点连流量为贡献的边，再向相关点连流量为 $inf$ 的边跑最小割即可。

1.13

$\color{Purple}\text{ P4313 文理分科\ \ \ \ \ }\color{Green}\text{No FST}$

同 $\color{Purple}\text{ P1646 [国家集训队] happiness}$。

$\color{Blue}\text{ P4016 负载平衡问题\ \ \ \ \ }\color{Green}\text{No FST}$

将货物数量与均值做差，多的向源点连边，少的向汇点连边，再根据花费连边跑费用流即可。

$\color{Purple}\text{ P1251 餐巾计划问题\ \ \ \ \ }\color{Green}\text{No FST}$

巧妙的建模。

考虑拆点，将每天拆成开始点与结束点，洗完后的结束点向下一次的开始点连快洗边、慢洗边和保存边，开始点向汇点连费用为 $0$，流量为 $r_i$ 的边保证每天毛巾用满，源点向结束点连费用为 $0$，流量为 $r_i$ 的边使得流出去的毛巾再流回来，源点向开始点连费用为 $p$，流量为 $r_i$ 的边表示买入，跑费用流即可。

1.14

$\color{Purple}\text{ P4582 [FJOI2014] 树的重心\ \ \ \ \ }\color{Red}\text{FST=9}$

先找出重心，令他（两个则任选一个）为根。

• 只有一个重心：

一个点为一棵树为唯一重心的充要条件是其每棵子树的大小都小于 $\frac{n}{2}$，设 $f_{i,j}$ 表示在以 $i$ 为根的子树内选择与 $i$ 联通的 $j$ 个点的方案数，$dp$ 出答案即可。

• 有两个重心：

一个点为一棵树为两重心的充要条件是另一个重心所在的子树的大小为 $\frac{n}{2}$，其他子树的大小都小于 $\frac{n}{2}$，同理进行 $dp$ 即可。

时间复杂度 $O(qn^3)$，足以通过此题，但可以发现 $dp$ 的底层是卷积的形式，故应该可以借助 $FFT$ 优化至 $O(qn^2)$。

1.15

$\color{Purple}\text{ CF342E Xenia and Tree\ \ \ \ \ }\color{Green}\text{No FST}$

对操作进行分块，对于块内的每一个询问，其答案只可能来自两个地方：

1. 本块之前加入的点。
2. 本块内询问前加入的点。

对于前者，我们在一个整块操作完后将块内加入的点进行多源 $bfs$ 求最短路，复杂度为 $O(n\sqrt n)$。

对于后者，暴力求距离即可，复杂度为 $O(n\sqrt n\log n)$。

1.16

$\color{Purple}\text{ P4516 [JSOI2018] 潜入行动\ \ \ \ \ }\color{Red}\text{FST=12}$

设 $f_{x,i,0/1,0/1}$ 表示 $x$ 的子树内放 $i$ 个监听设备，点 $x$ 放/不放，点 $x$ 被/不被覆盖的方案数，直接 dp 即可。

$\color{Purple}\text{ CF1442D Sum\ \ \ \ \ }\color{Red}\text{FST=1}$

对于两个序列，如果我们都只取前一段，由于序列是单调的，将其中一个序列的下一个值较大的取下也肯定更优，所以至多只有一个序列只取一部分，把其它序列整个当成物品 dp，再与本序列合并就可以得到 $O(n^3)$ 的做法。直接分治就能优化至 $O(nk\log n)$。

1.17

$\color{Purple}\text{ P8476 「GLR-R3」惊蛰\ \ \ \ \ }\color{Red}\text{FST=14}$

卡大常题，让我充分认识到了线段树的优化空间。

设 $f_{i,j}$ 表示确定了 $b_{1\sim i}$ 且 $b_i=j$ 的方案数，不难发现只有 $j=a_x$ 是有用的，于是改令 $f_{i,j}$ 表示确定了 $b_{1\sim i}$ 且 $b_i=c_j$ 的方案数，$c_j$ 表示 $a$ 数组离散化后的第 $j$ 小数。

显然有

$$f_{i,j}=\min\{\min_{k=j}^{a_i}f_{i-1,k}+C,\min_{k=a_i+1}^{c_n}f_{i-1,k}+a_k-a_i\}$$

不难发现 $f_{i,j}$ 随 $j$ 减少而减少，故只要将两个端点值取 $\min$ 即可。

可以用线段树维护。