「静态区间第k小值」SP3946 MKTHNUM - K-th Number

知识点: 主席树，整体二分

原题面 Luogu1 Luogu2

---

扯

寒假摸鱼摸爽了，重学整体二分= =

---

题意简述

给定一长度为 \(n\) 的数列 \(a\)，给定 \(m\) 次询问。
每次询问给定参数 \(l,r,k\)，查询数列 \(a\) 在闭区间 \([l,r]\) 内的第 \(k\) 小值。
\(1\le n,m\le 2\times 10^5\)，\(|a_i|\le 10^9\)，\(1\le l\le r\le n\)，\(1\le k\le r-l+1\)。

---

分析题意

经典问题经典解法。
先离散化，设数列最大值为 \(m\)。

---

考虑仅有一次询问的情况，yy 一下可得到这样一种解法：
对于区间 \([l,r]\)，考虑排名 \(<k\) 的数的数量。
考虑每次二分答案的值域 \([L, R]\)，并检查区间 \([l,r]\) 中，\(\le \dfrac{L+R}{2}\) 的数，即左侧的数的个数 \(size\)。
若 \(size<k\)，则答案一定在值域 \([L, mid]\) 中，下调右端点。
否则答案在 \([mid + 1, R]\) 中，且一定为其中排名第 \(k-size\) 的数，上调左端点。
区间长度收缩至 \(1\) 时即得答案。

暴力实现的单次复杂度是 \(O(n\log m)\) 的，和排序同级，比较傻逼。
但这给出了一种思路：二分值域并检查数量。
以下两种解法均按此思路展开。

---

主席树

看到二分值域检查数量，想到了权值线段树。
假设已知区间 \([l,r]\) 建出的权值线段树，上面的二分完全可以在线段树上进行。
对于某节点维护的区间 \([L,R]\)，其左右儿子分别维护的区间为 \([L,\dfrac{L+R}{2}]\)，\([\dfrac{L+R}{2} + 1, R]\)。
每次检查左儿子的数的数量 \(size\le k\) 是否成立。
若成立，则答案必在左儿子，向左儿子递归。
否则答案一定在右儿子，且一定是右儿子中排名 \(k-size\) 的数。
令 \(k- size\)，并向右儿子递归。
递归至叶节点即得答案。
上述过程复杂度是 \(O(\log m)\) 的，非常喜人。

---

想办法怎么得到权值线段树。
考虑权值线段树构造的过程，在 \([l,r]\) 的权值线段树上插入 \(a_{r+1}\)，即得 \([l,r+1]\) 的权值线段树。
这玩意的形式和前缀和有些相似，不妨强行凑一凑。
考虑 \([1,l-1]\) 和 \([1,r]\) 的权值线段树，将它们对应位置节点维护信息相减。
上述过程相当于删除 \([1,l-1]\) 的信息，可得到 \([l,r]\) 的权值线段树。
考虑将 \(1\sim x\) 的前缀权值线段树全建出来，树上二分时 再将对应位置节点维护信息相减。
单次查询的复杂度可以保证，但建树的时间和空间消耗较大。

发现 \([1,l]\) 和 \([1,l+1]\) 的权值线段树上，仅有 \(\log m\) 个节点不同。
考虑可持久化线段树的套路，动态开点，并利用之前的线段树的信息。
可以获得这样的结构：

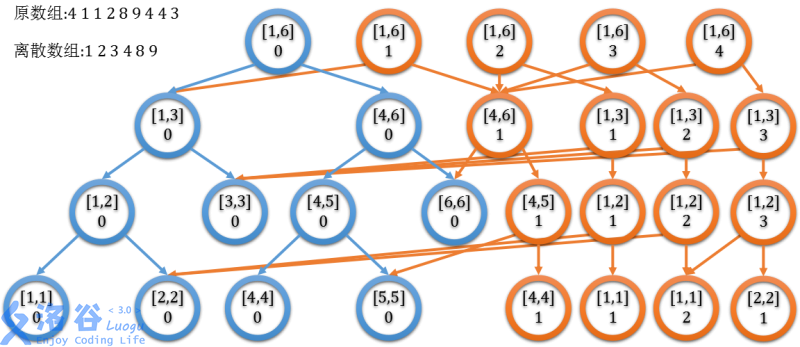
图片来源 主席树 - 孤独·粲泽 的博客。

然后就赢了。
空间复杂度 \(O(n\log m)\)，时间复杂度 \(O(q\log m)\)。

---

整体二分

整体二分实质上是对操作序列，按时间顺序进行二分。
先考虑单个询问如何二分，再进行拓展。
总复杂度一般是单次询问复杂度乘一个 \(\log\)。

考虑之前的暴力，调换一下检查对象。
为方便查询个数，维护一个树状数组。
二分值域 \([L, R]\)，遍历整个数列中所有 \(\le mid\) 的数，令其树状数组中对应下标位置 + 1。
检查区间 \([l, r]\) 内的元素个数 \(size\)。
若 \(size<k\)，则答案一定在值域 \([L, mid]\) 中，下调右端点。
否则答案在 \([mid + 1, R]\) 中，且一定为其中排名第 \(k-size\) 的数，上调左端点。
区间长度收缩至 \(1\) 时即得答案。

---

发现这样做便于检查多个询问，考虑把一堆询问放在一起二分。

具体地，将数列中的值看做单点修改操作，记录位置和权值，加到操作序列最前端，之后放入查询操作。
仍二分值域，但考虑把 答案在此权值区间 内的一堆操作放在一起二分。
设当前的值域为 \([L,R]\)，顺序枚举当前操作序列。
维护两个个 tmp 数组，称为左/右侧。

若当前操作为修改，且修改的值 \(\le mid\)，它应该被统计到 \(size\) 中，在树状数组它的位置处 + 1。并将其放入左侧。
否则 不进行操作，并将其放入右侧。

若为查询操作，检查 询问区间 \([l,r]\) 内的元素个数 \(size\)。
若 \(size<k\)，则答案一定在值域 \([L, mid]\) 中，将其放入左侧。
否则答案在 \([mid + 1, R]\) 中，且一定为其中排名第 \(k-size\) 的数，将询问的 \(k-size\)，并放入右侧。

之后同时考虑 \([L, mid]\) 和 \([mid + 1, R]\) 两个值域区间。
两值域区间对应的操作，即为上面维护的 左/ 右侧，分别递归进行即可。
区间长度收缩至 \(1\) 时，该权值区间内的所有查询操作，答案即可确定。

看起来这样挺假的，但并没有什么问题。
单拿出来每一个询问，其二分过程都是完整的。

建议阅读代码加深理解。

正常写法空间复杂度 \(O(n)\)，时间复杂度 \(O(q\log^2 m)\)。

---

代码实现

整体二分

//知识点：整体二分 
/*
By:Luckyblock
*/
#include <algorithm>
#include <cstdio>
#include <ctype.h>
#include <cstring>
#define ll long long
const int kMaxn = 4e5 + 10; 
//=============================================================
struct Operation {
  bool type;
  int l, r, k, id;
  int val, pos;
} q[kMaxn], lq[kMaxn], rq[kMaxn];
int n, m, maxa, a[kMaxn], data[kMaxn], map[kMaxn], ans[kMaxn];
//=============================================================
inline int read() {
  int f = 1, w = 0;
  char ch = getchar();
  for (; !isdigit(ch); ch = getchar())
    if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
void GetMax(int &fir_, int sec_) {
  if (sec_ > fir_) fir_ = sec_;
}
void GetMin(int &fir_, int sec_) {
  if (sec_ < fir_) fir_ = sec_;
}
namespace TreeArray {
  #define lowbit(x) (x&-x)
  const int kMaxm = 2e5;
  int time, ti[kMaxm + 10], t[kMaxm + 10];
  void Clear() {
    time ++;
  }
  void Add(int pos_, int val_) {
    for (; pos_ <= n; pos_ += lowbit(pos_)) {
      if (ti[pos_] < time) {
        t[pos_] = 0;
        ti[pos_] = time;
      }
      t[pos_] += val_;
    }
  }
  int Sum(int pos_) {
    int ret = 0;
    for (; pos_; pos_ -= lowbit(pos_)) {
      if (ti[pos_] < time) {
        t[pos_] = 0;
        ti[pos_] = time;
      }
      ret += t[pos_];
    }
    return ret;
  }
}
void Prepare() {
  n = read(), m = read();
  for (int i = 1; i <= n; ++ i) {
    data[i] = a[i] = read();
  }
  std :: sort(data + 1, data + n + 1);
  int lth = std :: unique(data + 1, data + n + 1) - data - 1;
  for(int i = 1; i <= n; i ++) {
    int ori = a[i];
    a[i] = std :: lower_bound(data + 1, data + lth + 1, ori) - data;
    map[a[i]] = ori;
    GetMax(maxa, a[i]);
  }
}
#define mid ((l_+r_)>>1)
void Solve(int l_, int r_, int ql_, int qr_) {
  if (ql_ > qr_) return ;
  if (l_ == r_) {
    for (int i = ql_; i <= qr_; ++ i) {
      if (q[i].type) ans[q[i].id] = l_;
    }
    return ;
  }
  
  int pl = 0, pr = 0;
  for (int i = ql_; i <= qr_; ++ i) {
    if (! q[i].type) {
      if (q[i].val <= mid) {
        TreeArray :: Add(q[i].pos, 1);
        lq[++ pl] = q[i];
      } else {
        rq[++ pr] = q[i];
      }
    } else {
      int ret = TreeArray :: Sum(q[i].r) - TreeArray :: Sum(q[i].l - 1);
      if (q[i].k <= ret) {
        lq[++ pl] = q[i];
      } else {
        q[i].k -= ret;
        rq[++ pr] = q[i];
      }
    }
  }
  TreeArray :: Clear();
  for (int i = 1; i <= pl; ++ i) q[ql_ + i - 1] = lq[i];
  for (int i = 1; i <= pr; ++ i) q[ql_ + pl + i - 1] = rq[i];
  Solve(l_, mid, ql_, ql_ + pl - 1);
  Solve(mid + 1, r_, ql_ + pl, qr_);
}
//=============================================================
int main() {
  Prepare();
  for (int i = 1; i <= n; ++ i) {
    q[i] = (Operation) {false, 0, 0, 0, 0, a[i], i};
  }
  for (int i = 1; i <= m; ++ i) {
    q[n + i] = (Operation) {true, read(), read(), read(), i, 0, 0};
  }
  Solve(1, maxa, 1, n + m);
  for (int i = 1; i <= m; ++ i) {
    printf("%d\n", map[ans[i]]);
  }
  return 0;
}

---

另一种二分写法，时间不变空间较劣，但很好写（大雾

//知识点：整体二分
/*
By:Luckyblock
*/
#include <algorithm>
#include <cstdio>
#include <ctype.h>
#include <cstring>
#include <vector>
#define ll long long
const int kMaxn = 4e5 + 10; 
//=============================================================
struct Number {
  int pos, val;
};
struct Query {
  int l, r, k, id;
};
int n, m, maxa, a[kMaxn], data[kMaxn], map[kMaxn], ans[kMaxn];
//=============================================================
inline int read() {
  int f = 1, w = 0;
  char ch = getchar();
  for (; !isdigit(ch); ch = getchar())
    if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
void GetMax(int &fir_, int sec_) {
  if (sec_ > fir_) fir_ = sec_;
}
void GetMin(int &fir_, int sec_) {
  if (sec_ < fir_) fir_ = sec_;
}
namespace TreeArray {
  #define lowbit(x) (x&-x)
  const int kMaxm = 2e5;
  int time, ti[kMaxm + 10], t[kMaxm + 10];
  void Clear() {
    time ++;
  }
  void Add(int pos_, int val_) {
    for (; pos_ <= n; pos_ += lowbit(pos_)) {
      if (ti[pos_] < time) {
        t[pos_] = 0;
        ti[pos_] = time;
      }
      t[pos_] += val_;
    }
  }
  int Sum(int pos_) {
    int ret = 0;
    for (; pos_; pos_ -= lowbit(pos_)) {
      if (ti[pos_] < time) {
        t[pos_] = 0;
        ti[pos_] = time;
      }
      ret += t[pos_];
    }
    return ret;
  }
}
void Prepare() {
  n = read(), m = read();
  for (int i = 1; i <= n; ++ i) {
    data[i] = a[i] = read();
  }
  std :: sort(data + 1, data + n + 1);
  data[0] = - 0x3f3f3f3f;
  for (int i = 1; i <= n; ++ i) {
    if (data[i] != data[i - 1]) map[++ maxa] = data[i]; 
    data[maxa] = data[i];
  }
  for (int i = 1; i <= n; ++ i) {
    a[i] = std :: lower_bound(data + 1, data + maxa + 1, a[i]) - data;
  }
}
#define mid ((l_+r_)>>1)
void Solve(int l_, int r_, std :: vector <Number> num_, std :: vector <Query> q_) {
  if (l_ == r_) {
    for (int i = 0, size = q_.size(); i < size; ++ i) {
      ans[q_[i].id] = l_;
    }
    return ;
  }
  std :: vector <Number> numl, numr;
  std :: vector <Query> ql, qr;
  for (int i = 0, size = num_.size(); i < size; ++ i) {
    if (num_[i].val <= mid) {
      numl.push_back(num_[i]);
      TreeArray :: Add(num_[i].pos, 1);
    } else {
      numr.push_back(num_[i]);
    }
  }
  for (int i = 0, size = q_.size(); i < size; ++ i) {
    int suml = TreeArray :: Sum(q_[i].r) - TreeArray :: Sum(q_[i].l - 1);
    if (q_[i].k <= suml) {
      ql.push_back(q_[i]); 
    } else {
      q_[i].k -= suml;
      qr.push_back(q_[i]);
    }
  }
  TreeArray :: Clear();
  Solve(l_, mid, numl, ql);
  Solve(mid + 1, r_, numr, qr);
}
//=============================================================
int main() {
  Prepare();
  std :: vector <Query> q;
  std :: vector <Number> num;
  for (int i = 1; i <= n; ++ i) {
    num.push_back((Number) {i, a[i]});
  }
  for (int i = 1; i <= m; ++ i) {
    q.push_back((Query){read(), read(), read(), i});
  }
  Solve(1, maxa, num, q);
  for (int i = 1; i <= m; ++ i) {
    printf("%d\n", map[ans[i]]);
  }
  return 0;
}

---

主席树

早期变量取名风格 + 写法。

//知识点：主席树
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstdlib>
#define ls (t[now].L)
#define rs (t[now].R)
#define ll long long
const int MARX = 3e5 + 10;
//=============================================================
struct TheScientificConceptOfDevelopmentTree {
  int L, R, size;
} t[MARX << 5];
int N, M, Data[MARX], Val[MARX], Map[MARX];
int NodeNum, Root[MARX];
//=============================================================
inline int read() {
  int f = 1, w = 0;
  char ch = getchar();
  for (; !isdigit(ch); ch = getchar())
    if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
void Build(int &now, int L, int R) {
  now = ++NodeNum;
  if (L >= R) return;
  int mid = (L + R) >> 1;
  Build(ls, L, mid);
  Build(rs, mid + 1, R);
}
void Update(int Pre, int &now, int L, int R, int Value) {
  now = ++NodeNum;
  t[now].size = t[Pre].size + 1;
  ls = t[Pre].L, rs = t[Pre].R;

  if (L >= R) return;
  int mid = (L + R) >> 1;
  if (Value > mid)
    Update(t[Pre].R, rs, mid + 1, R, Value);
  else
    Update(t[Pre].L, ls, L, mid, Value);
}
int Query(int U, int V, int L, int R, int Key) {
  if (L == R) return L;
  int Size = t[t[V].L].size - t[t[U].L].size;
  int mid = (L + R) >> 1;
  if (Key <= Size) return Query(t[U].L, t[V].L, L, mid, Key);
  return Query(t[U].R, t[V].R, mid + 1, R, Key - Size);
}
//=============================================================
int main() {
  N = read(), M = read();
  for (int i = 1; i <= N; i++) Data[i] = Val[i] = read();
  std ::sort(Data + 1, Data + N + 1);
  int Lth = std ::unique(Data + 1, Data + N + 1) - Data - 1;
  for (int i = 1; i <= N; i++) {
    int Oringinal = Val[i];
    Val[i] = std ::lower_bound(Data + 1, Data + Lth + 1, Val[i]) - Data;
    Map[Val[i]] = Oringinal;
  }

  Build(Root[0], 1, N);
  for (int i = 1; i <= N; i++) Update(Root[i - 1], Root[i], 1, N, Val[i]);
  for (int i = 1; i <= M; i++) {
    int L = read(), R = read(), K = read();
    printf("%d\n", Map[Query(Root[L - 1], Root[R], 1, N, K)]);
  }
  return 0;
}