「笔记」二分图
写在前面 :
\(\text{Thanks for wikipedia}\)
\(\text{Thanks for OI-Wiki}\)
\(\text{Thanks for Luogu}\)
定义 及 性质
-
二分图 :
二分图的顶点可分成 两互斥的独立集 \(U\) 和 \(V\) , 使得所有边都连结一个 \(U\) 中的点和一个 \(V\) 中的点 .
顶点集 \(U, V\) 被称为是图的两个部分.
等价的 , 二分图 可以被定义成 图中所有的环都有偶数个顶点 .
\[\text{图 1} \]如图 \(1\) , 可将\(U\) 和\(V\) 当做一个着色 :
\(U\) 中所有顶点为蓝色 , \(V\) 中所有顶点着绿色 , 每条边的两个端点的颜色不同, 符合图着色问题的要求 .
\[\text{图 2} \]相反的 , 非二分图无法被二着色 ,
如图 \(2\) , 将其中一顶点着蓝色 且另一着绿色后 , 第三个顶点 与上述具有两颜色的顶点相连 , 无法再对它着蓝色或绿色 . -
匹配 :
给定一张图 G , 在 G的一子图 M 中 , M 的边集中的任意两条边都没有共同的端点 , 则称 M是一个匹配
对于图 \(1\) 所示二分图 , 图 \(3\) 的选择方案 , 即为 图 \(1\)的一匹配
\[\text{图 3} \] -
最大匹配:
给定一张图 \(G\) , 其中边数最多的匹配 , 即该图的最大匹配
对于图 \(1\) 所示二分图 , 图 \(4\) 的选择方案 , 即为 图 \(1\)的一最大匹配
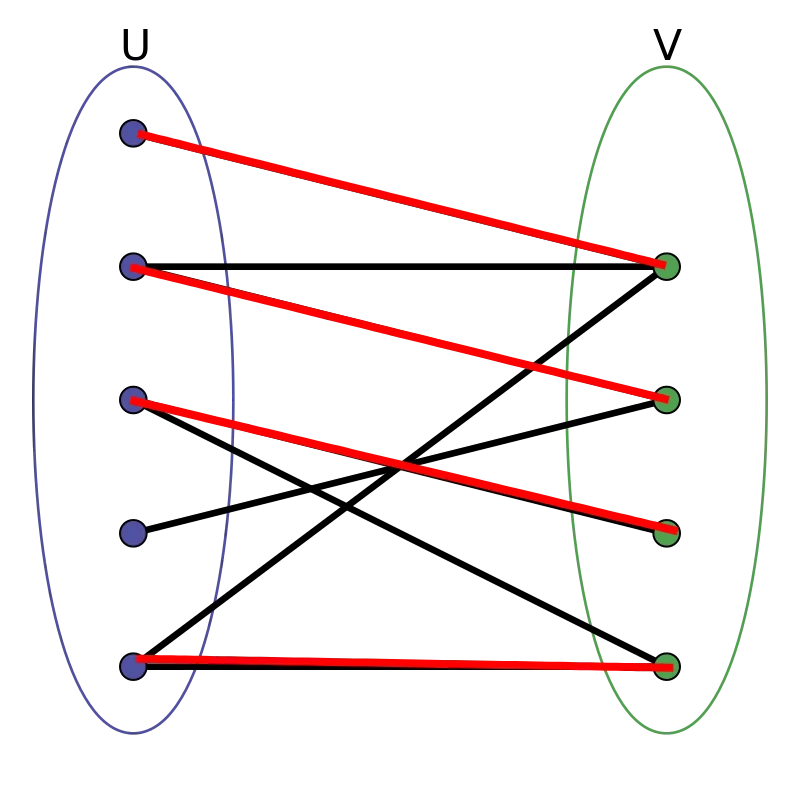\[\text{图 4} \]最大匹配可能不唯一 , 但最大匹配的边数确定 , 且不可能超过图中顶点 数的一半 .
根据匹配的性质 , 一匹配中 不同边对应的两对顶点 完全不同 , 否则它们相邻 , 不满足匹配的定义 -
二分图的最小顶点覆盖 :
最小顶点覆盖要求用最少的点 , 让每条边都至少和其中一个点关联 .
\(\text{Knoig}\) 定理 : 二分图的最小顶点覆盖数等于二分图的最大匹配数 . -
二分图的最大独立集 :
在 \(n\) 个点的图 \(G\) 中选出 \(m\) 个点 , 使这 \(m\) 个点两两之间没有连边 , 求\(m\) 最大值 .
引理 : 二分图的最大独立集数 = 节点数(\(n\)) — 最大匹配数(\(m\))
二分图判断 :
模板题 : https://vjudge.net/problem/HihoCoder-1121
通过 二分图可被二着色的性质可得 ,
一个无向图是否为 二分图 , 可通过 \(dfs / bfs\) 染色 , 来进行判断 .
对于图中每一联通块 , 任选其中一点 , 将其染为绿色
显然 , 为满足每一条边两端点颜色都不同 , 与选择点相连的点 都应被染为蓝色
则可使用 \(bfs\)进行模拟染色 :
- 对于一 与当前结点联通, 未被染色的点 , 将其染为 与当前结点相反色
- 对于一 与当前结点联通, 已被染色的点 , 若其颜色与 当前结点相同 , 则不合法, 该图不为 二分图
\(dfs\) 与 \(bfs\) 的复杂度 都为\(O(n)\) , 为避免出现递归爆栈情况 , 一般使用 \(bfs\)
\(dfs\) 实现 :
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
const int MAX_V = 205;
vector<int> G[MAX_V]; // 图
int V; // 顶点数
int color[MAX_V]; // 顶点i的颜色 1 或 -1
// 把顶点染成1或-1
bool dfs(int v, int c)
{
color[v] = c; // 把顶点v染成颜色c
for (int i = 0; i < G[v].size(); ++i) {
if (color[G[v][i]] == c) return false;
if (color[G[v][i]] == 0 && !dfs(G[v][i], -c)) return false;
}
return true;
}
void solve()
{
for (int i = 0; i < V; ++i) {
if (color[i] == 0) {
if (!dfs(i, 1)) {
puts("Wrong\n");
return ;
}
}
}
puts("Correct\n");
}
int main()
{
int E;
while (scanf("%d%d", &V, &E) == 2) {
int a, b;
for (int i = 0; i < V; ++i) G[i].clear();
memset(color, 0, sizeof color);
for (int i = 0; i < E; ++i) {
scanf("%d%d", &a, &b);
G[a].push_back(b);
G[b].push_back(a);
}
solve();
}
return 0;
}
\(bfs\) 实现 :
//By:Luckyblock
#include <cstdio>
#include <cstring>
#include <queue>
#include <ctype.h>
const int MARX = 1e4 + 10;
//=============================================================
struct edge
{
int u, v, ne;
}e[MARX << 3];
int num, T, N, M, head[MARX], color[MARX];
//=============================================================
inline int read()
{
int s = 1, w = 0; char ch = getchar();
for(; !isdigit(ch); ch = getchar()) if(ch == '-') s = -1;
for(; isdigit(ch); ch = getchar()) w = (w << 1) + (w << 3) + (ch ^ '0');
return s * w;
}
inline void add(int u, int v)
{
e[++ num].v = v, e[num].u = u;
e[num].ne = head[u], head[u] = num;
}
bool bfs()
{
for(int i = 1; i <= N; i ++)
if(head[i] && color[i] == 0)//找到未被染色的 联通块
{
std :: queue <int> q;
while (!q.empty()) q.pop();
q.push(i); color[i] = 1;//对起点 进行染色
while(! q.empty())
{
int u = q.front(); q.pop();
for(int j = head[u]; j; j = e[j].ne)
{
int v = e[j].v;
if(color[v] == color[u]) return 0;//一边两端点 颜色相同 , 则不合法
if(! color[v]) color[v] = - color[u], q.push(v);// 染为相反色
}
}
}
return 1;
}
//=============================================================
signed main()
{
T = read();
while(T --)
{
num = 0;
memset(head, 0, sizeof(head));
memset(color, 0, sizeof(color));
N = read(), M = read();
bool flag = 1;
for(int i = 1; i <= M; i ++)
{
int u = read(), v = read();
add(u, v), add(v, u);
}
if(bfs()) printf("Correct\n");
else printf("Wrong\n");
}
}
二分图 最大匹配
-
匈牙利算法 :
-
算法核心
对于一匹配 \(M\) ,
增广路径是指从 \(M\) 中未使用的顶点开始 , 并从 \(M\) 中未使用的顶点结束的交替路径 .
可以证明 , 一个匹配是最大匹配 , 当且仅当它没有任何增广路经匈牙利算法的核心 即寻找增广路径 , 它是一种用增广路径 求 二分图最大匹配的算法
-
算法流程 :
先将给定二分图分为 \(U\) , \(V\) 两独立集 , 枚举 \(U\) 中结点
对当前枚举\(U\) 中结点 \(u\), 枚举其相邻 的\(V\) 中结点 \(v\)
-
若 \(v\) 没有与任一 \(U\) 中其他结点配对 , 说明 \(E(u,v)\) 为一增广路 , 则可直接加入 最大匹配中
-
否则 , 枚举 \(v\) 相邻的 \(U\)中结点 , 递归检查 \(v\) 点的匹配点 是否可与其他 \(V\)中结点 配对 .
若可以 , 则 \(u\) 可与 \(v\) 点进行匹配 , 加入最大匹配中
否则 , \(u\) 不可与 \(v\) 匹配 , \(u\) 点无匹配点 , 不可加入最大匹配中
-
-
手动模拟 :
写的太垃圾看不懂 ? 手玩一组数据试试 :
\[\text{图 5} \]
-
对 Yugari 进行匹配 :
其直接连接点 Reimu 未被匹配 , 则将 Yugari 与 Reimu 进行匹配 -
对 Marisa 进行匹配 :
其直接连接点 Patchouli 未被匹配 , 则将 Marisa 与 Patchouli 进行匹配 -
对 Suika 进行匹配 :
其直接连接点 Reimu 被匹配 , 检查 Reimu 的匹配点 Yugari 能否寻找到其他匹配点- Yugari 可与 Yuyuko 进行匹配 , 则将 Yugari 与 Yuyuko 进行匹配
由于Yugari 匹配对象改变 , Reimu 未被匹配 , 则将 Suika与 Reimu 进行匹配
-
对 Aya 进行匹配 :
其直接连接点 Reimu 被匹配 , 检查 Reimu 的匹配点 Suika 能否寻找到其他匹配点
- Suika 无其他匹配点 , 不可将 Suika 与其他结点进行匹配
由于Suika 匹配对象不可改变 , Reimu 被匹配 , 则 Aya 无匹配点
则此二分图的一种最大匹配为 :
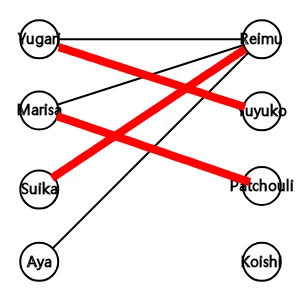\[\text{图 6} \]-
例题 :
-
模板题
//By:Luckyblock #include <cstdio> #include <cstring> #include <ctype.h> #define ll long long const int MARX = 1e3 + 10; const int MARX1 = 1e7 + 10; //============================================================= struct edge { int u, v, ne; }e[MARX1]; int N, M, E, num, ans, head[MARX], match[MARX]; bool vis[MARX]; //============================================================= inline int read() { int s = 1, w = 0; char ch = getchar(); for(; !isdigit(ch); ch = getchar()) if(ch == '-') s = -1; for(; isdigit(ch); ch = getchar()) w = (w << 1) + (w << 3) + (ch ^ '0'); return s * w; } void add(int u, int v) { e[++ num].u = u, e[num].v = v; e[num].ne = head[u], head[u] = num; } bool dfs(int u)//匈牙利算法配对 { for(int i = head[u]; i; i = e[i].ne)//枚举能到达的点 if(! vis[e[i].v])//在此轮配对中未被访问 { vis[e[i].v] = 1; if(! match[e[i].v] || dfs(match[e[i].v]))//若可配对 { match[e[i].v] = u;//更新 return 1; } } return 0; } //============================================================= signed main() { N = read(), M = read(), E = read(); for(int i = 1; i <= E; i ++) { int u = read(), v = read(); if(u > N || v > M) continue; add(u, v); } for(int i = 1; i <= N; i ++)//枚举一组中的N个点 { memset(vis, 0, sizeof(vis));//初始化 if(dfs(i)) ans ++;//可以将i点 加入匹配中 } printf("%d", ans); }-
二分图匹配 模板 , 使用匈牙利算法
题目要求输出方案
显然 , 没有匹配对象的点 , 其匹配对象为 0
将匹配完成后 各点的非0匹配对象输出即可
//By:Luckyblock #include <cstdio> #include <cstring> #include <ctype.h> #define ll long long const int MARX = 1e3 + 10; const int MARX1 = 1e7 + 10; //============================================================= struct edge { int u, v, ne; }e[MARX1]; int N, M, E, num, ans, head[MARX], match[MARX]; bool vis[MARX]; //============================================================= inline int read() { int s = 1, w = 0; char ch = getchar(); for(; !isdigit(ch); ch = getchar()) if(ch == '-') s = -1; for(; isdigit(ch); ch = getchar()) w = (w << 1) + (w << 3) + (ch ^ '0'); return s * w; } void add(int u, int v) { e[++ num].u = u, e[num].v = v; e[num].ne = head[u], head[u] = num; } bool dfs(int u)//匈牙利算法配对 { for(int i = head[u]; i; i = e[i].ne)//枚举能到达的点 if(! vis[e[i].v])//在此轮配对中未被访问 { vis[e[i].v] = 1; if(! match[e[i].v] || dfs(match[e[i].v]))//若可配对 { match[e[i].v] = u; //更新 return 1; } } return 0; } //============================================================= signed main() { N = read(), M = read(); while(1) { int u = read(), v = read(); if(u == -1 && v == -1) break; add(u, v); } for(int i = 1; i <= N; i ++)//枚举一组中的N个点 { memset(vis, 0, sizeof(vis));//初始化 if(dfs(i)) ans ++;//可以将i点 加入匹配中 } printf("%d\n", ans); for(int i = N + 1; i <= M; i ++)//输出方案 if(match[i]) printf("%d %d\n", match[i], i); }-
P4304 [TJOI2013]攻击装置 ( P3355 骑士共存问题 )
-
题目要求 :
给定一 \(01\) 矩阵 , 可在 \(0\) 的位置 放置攻击装置.
攻击装置 \((x,y)\) 可按照 "日" 字攻击其周围的 \(8\) 个位置
\((x-1,y-2), (x-2,y-1), (x+1,y-2), (x+2,y-1), (x-1,y+2), (x-2,y+1), (x+1,y+2), (x+2,y+1)\)
求在装置互不攻击的情况下 , 最多可以放置多少个装置 . -
分析题意 :
若将矩阵上每格看做一结点 , 向其可攻击位置连边
建图后, 则题目转化为 : 求给定图的 最大独立集由于题目给定了一张棋盘图 ,
可将棋盘黑白染色, 使相邻两格子不同色 .
观察图形发现 , 对于每一个格子, 其能够攻击到的位置 颜色一定与其不同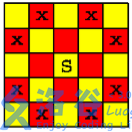
将格点转化为结点后 , 按照染色的不同, 可将各点分为两点集
可以发现 , 对于每一个点集之间没有连边 , 即每一个点集都为一独立集
则原棋盘图转化为 一二分图对于一二分图, 其最大独立集 = 节点数 \((n)\) \(—\) 最大匹配数 \((m)\)
可使用 求得最大匹配数 , 即得答案
-
#include <cstdio> #include <queue> #include <cstring> #include <vector> #include <ctype.h> #define ll long long int ex[10] = {2, -2, 2, -2, -1, 1, -1, 1};//坐标变化量 int ey[10] = {1, 1, -1, -1, 2, 2, -2, -2}; const int MARX = 4e4 + 10; const int MARX1 = 3e7 + 10; //============================================================= struct edge { int u, v, ne; }e[MARX1]; int N, num, node, ans, head[MARX], color[210][210], match[MARX]; bool map[210][210], vis[MARX]; std :: vector <int> U; //============================================================= inline int read() { int s = 1, w = 0; char ch = getchar(); for(; !isdigit(ch); ch = getchar()) if(ch == '-') s = -1; for(; isdigit(ch); ch = getchar()) w = (w << 1) + (w << 3) + (ch ^ '0'); return s * w; } void add(int u, int v) { e[++ num].u = u, e[num].v = v; e[num].ne = head[u], head[u] = num; } bool dfs(int u)//匈牙利算法 { for(int i = head[u]; i; i = e[i].ne)//枚举能到达的点 if(! vis[e[i].v])//在此轮配对中未被访问 { vis[e[i].v] = 1;//标记 if(! match[e[i].v] || dfs(match[e[i].v]))//若可配对 { match[e[i].v] = u;//更新 答案 return 1; } } return 0; } //============================================================= signed main() { N = read(); for(int i = 1; i <= N; i ++) { char tmp[210]; scanf("%s", tmp + 1); for(int j = 1; j <= N; j ++) { map[i][j] = (tmp[j] == '0');// 判断一格点是否可放置装置 node += map[i][j]; //更新总可使用格点数 color[i][j] = (i + j) % 2 ? 1 : -1;//对棋盘按照奇偶性 黑白染色 } } for(int i = 1; i <= N; i ++)//枚举坐标 for(int j = 1; j <= N; j ++) if(map[i][j]) for(int k = 0; k < 8; k ++)//枚举 可攻击的点 { if(i + ex[k] < 1 || i + ex[k] > N || j + ey[k] < 1 || j + ey[k] > N) continue; if(! map[i + ex[k]][j + ey[k]]) continue; add((i - 1) * N + j, (i + ex[k] - 1) * N + j + ey[k]);//连边 } for(int i = 1; i <= N; i ++)//将染为 1的点加入点集 for(int j = 1; j <= N; j ++) if(map[i][j] && color[i][j] == 1) U.push_back((i - 1) * N + j); for(int i = 0, size = U.size(); i < size; i ++)//枚举一独立集中的点 { memset(vis, 0, sizeof(vis)); if(dfs(U[i])) ans ++;//进行配对 } printf("%d", node - ans);//求得 最大独立集 } -
-
-
网络流 :
-
算法核心:
在一个匹配中, 任意两条边都没有共同的端点.
每一个端点 最多只有 1 的贡献.在网络流中, 最多只有 1 的贡献, 可转化为 边的容量为 1.
由此可对原二分图进行转化:- 新建源点 与 汇点.
- 源点向每个左侧点 各连一条容量为 1 的有向边.
- 原图中的边改为 自左向右的有向边, 容量为 1.
- 每个右侧点向汇点 各连一条容量为 1 的有向边.
\[\text{图 7} \]强制使每一条边,每一个点 贡献至多为1.
使用网络最大流算法, 求得源点至汇点的最大流, 即为答案.P3386 【模板】二分图匹配 Dinic:
//知识点:网络流 /* By:Luckyblock 使用了当前弧优化. 边从0开始编号的原因: 0 ^ 1 = 1, 1 ^ 1 = 0, 1 ^ 1 != 2 每一次有流量汇入 == 成功匹配 */ #include <cstdio> #include <cctype> #include <algorithm> #include <cstring> #include <queue> #define min std::min #define ll long long const int MARX = 1e7 + 10; const int INF = 2e9 + 10; //=========================================================== struct Edge { int u, v, w, ne; } e[MARX << 1]; int N, M, E, S, T, edgenum = - 1, head[MARX]; int Dep[MARX], cur[MARX]; //=========================================================== inline int read() { int f = 1, w = 0; char ch = getchar(); for(; ! isdigit(ch); ch = getchar()) if(ch == '-') f = - 1; for(; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0'); return f * w; } void AddEdge(int u, int v, int w) { e[++ edgenum].u = u, e[edgenum].v = v, e[edgenum].w = w; e[edgenum].ne = head[u], head[u] = edgenum; } bool Bfs() { std :: queue <int> Q; memset(Dep, 0 ,sizeof(Dep)); Dep[S] = 1; Q.push(S); do { int u = Q.front(); Q.pop(); for(int i = head[u]; i != - 1; i = e[i].ne) if(e[i].w > 0 && Dep[e[i].v] == 0) Dep[e[i].v] = Dep[u] + 1, Q.push(e[i].v); } while(! Q.empty()); return Dep[T]; } int Dfs(int u, int dis) { if(u == T) return dis; for(int& i = cur[u]; i != - 1; i = e[i].ne) if(Dep[e[i].v] == Dep[e[i].u] + 1 && e[i].w) { int ret = Dfs(e[i].v, min(dis, e[i].w)); if(ret > 0) { e[i].w -= ret, e[i ^ 1].w += ret; return ret; } } return 0; } int Dinic() { int ans = 0; while(Bfs()) { for(int i = 0; i <= N + M + 1; i ++) cur[i] = head[i]; while(int ret = Dfs(S, INF)) ans += ret; } return ans; } //=========================================================== int main() { N = read(), M = read(), E = read(), S = 0, T = N + M + 1; memset(head, - 1, sizeof(head)); for(int i = 1; i <= N; i ++) AddEdge(0, i, 1), AddEdge(i, 0, 0); for(int i = N + 1; i <= N + M; i ++) AddEdge(i, T, 1), AddEdge(T, i, 0); for(int i = 1; i <= E; i ++) { int u = read(), v = read(); if(u > N || v > M) continue; AddEdge(u, v + N, 1), AddEdge(v + N, u, 0); } printf("%d", Dinic()); return 0; } -
写在后面 :
关于二分图最大匹配的样例解释 :
你知道在一张完全图里抠出一张二分图有多难吗
2020.6.13: 好像Yukari写成yugari了= =希望不要被隙ejwopidmwadklawhdiowh
