算法和数据结构

算法基础

算法概念

算法（Algorithm）：⼀个计算过程，解决问题的⽅法

Niklaus Wirth: “程序=数据结构+算法”

时间复杂度

时间复杂度-小结

• 时间复杂度是⽤来估计算法运⾏时间的⼀个式⼦（单位）。
• ⼀般来说，时间复杂度⾼的算法⽐复杂度低的算法慢。
• 常⻅的时间复杂度（按效率排序）
• O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)
• 复杂问题的时间复杂度
• O(n!) O(2n) O(nn) …

空间复杂度

空间复杂度：⽤来评估算法内存占⽤⼤⼩的式⼦

空间复杂度的表示⽅式与时间复杂度完全⼀样

算法使⽤了⼏个变量：O(1)

算法使⽤了⻓度为n的⼀维列表：O(n)

算法使⽤了m⾏n列的⼆维列表：O(mn)

“空间换时间”

复习：递归

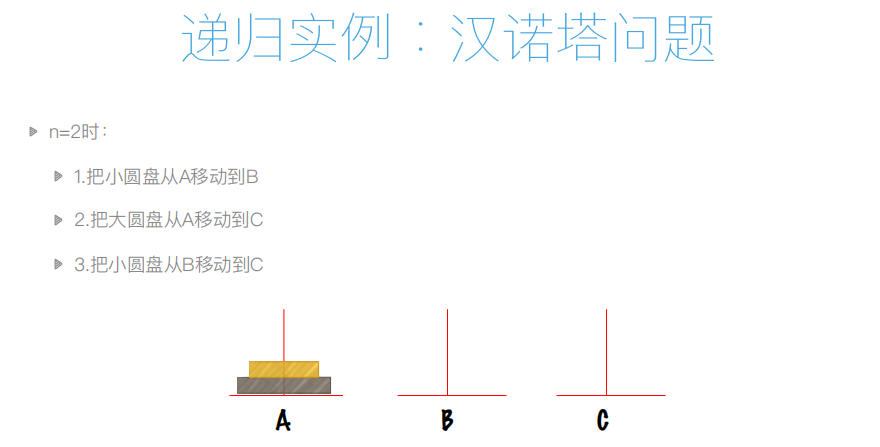
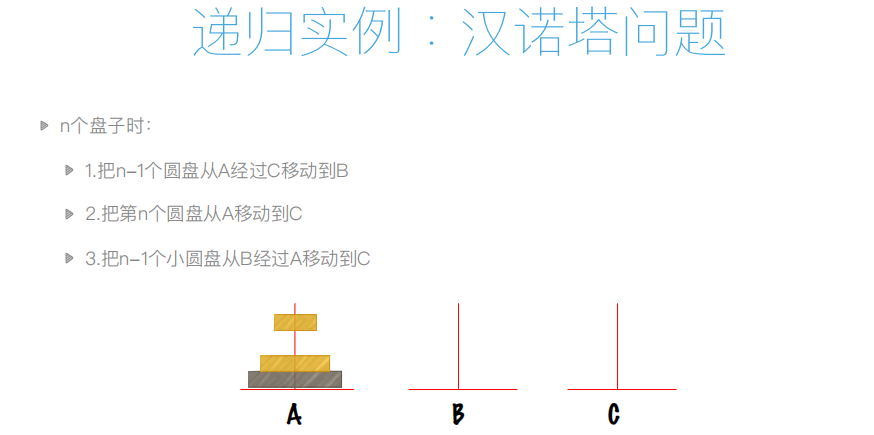
递归实例：汉诺塔问题

查找排序

查找

查找:在⼀些数据元素中，通过⼀定的⽅法找出与给定关键字相同的数据元素的过程。

列表查找(线性列表查找)：从列表中查找指定元素

• 输⼊：列表、待查找元素
• 输出：元素下标（未找到元素时⼀般返回None或-1）

内置列表查找函数：index()

顺序查找

二分查找

⼆分查找：⼜叫折半查找，从有序列表的初始候选区li[0:n]开始，通过对待查找的值与候选区中间值的⽐较，可以使候选区减少⼀半。

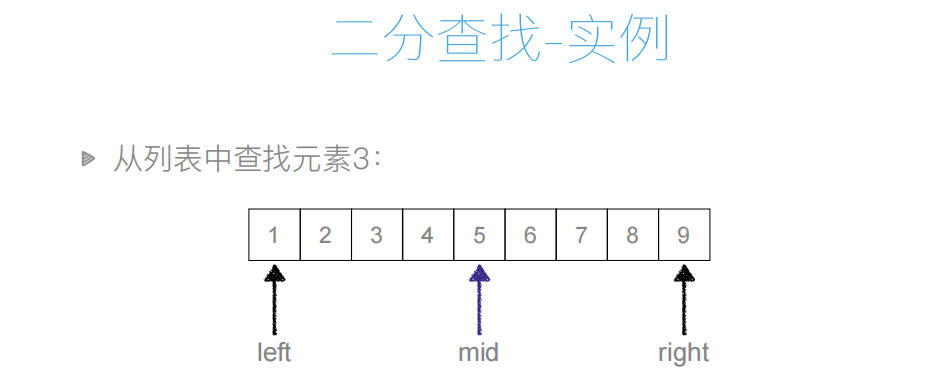
二分查找和线性查找速度比较

"""计算时间的装饰器"""
import time

def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__, t2 - t1))
        return result
    return wrapper
"""计算时间的装饰器"""
from cal_time import *

# 线性查找
@cal_time
def linear_search(li, val):
    for ind, v in enumerate(li):
        if v == val:
            return ind
    else:
        return None

# 二分查找
@cal_time
def binary_search(li, val):
    left = 0
    right = len(li) - 1
    while left <= right:    # 候选区有值
        mid = (left + right) // 2
        if li[mid] == val:
            return mid
        elif li[mid] > val: # 带查找的值在mid左侧
            right = mid - 1
        else: # li[mid] < val 带查找的值在mid右侧
            left = mid + 1
    else:
        return None
li = list(range(1000000))
linear_search(li, 38900)
binary_search(li, 38900)
# ---------------------run result-------------------
linear_search running time: 0.015621423721313477 secs.
binary_search running time: 0.0 secs.

排序

什么是列表排序

排序：将⼀组“⽆序”的记录序列调整为“有序”的记录序列。

列表排序：将⽆序列表变为有序列表

• 输⼊：列表
• 输出：有序列表

升序与降序

内置排序函数：sort()

常⻅排序算法介绍

常见排序算法分析

冒泡排序 (Bubble Sort)

列表每两个相邻的数，如果前⾯⽐后⾯⼤，则交换这两个数。

⼀趟排序完成后，则⽆序区减少⼀个数，有序区增加⼀个数。

代码关键点：趟、⽆序区范围

选择排序 (Select Sort)

⼀趟排序记录最⼩的数，放到第⼀个位置

再⼀趟排序记录记录列表⽆序区最⼩的数，放到第⼆个位置

……

算法关键点：有序区和⽆序区、⽆序区最⼩数的位置

def select_sort(li):
    for i in range(len(li)-1): # i是第几趟
        min_loc = i
        for j in range(i+1, len(li)):
            if li[j] < li[min_loc]:
                min_loc = j
        li[i], li[min_loc] = li[min_loc], li[i]
        print(li)

li = [3,4,2,1,5,6,8,7,9]
print(li)
select_sort(li)

插入排序

def insert_sort(li):
    for i in range(1, len(li)): #i 表示摸到的牌的下标
        tmp = li[i]
        j = i - 1 #j指的是手里的牌的下标
        while j >= 0 and li[j] > tmp:
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp
        print(li)
li = [3,2,4,1,5,7,9,6,8]
print(li)
insert_sort(li)

快速排序

def partition(li, left, right):
    tmp = li[left]
    while left < right:
        while left < right and li[right] >= tmp:  # 从右面找比tmp小的数
            right -= 1  # 往左走一步
        li[left] = li[right]  # 如果右边的数比左边的数小，就把右边的值写到左边空位上
        # print(li, 'right')
        while left < right and li[left] <= tmp:
            left += 1
        li[right] = li[left]  # 如果左边的数比右边的数大，就把左边的值写到右边空位上
        # print(li, 'left')
    li[left] = tmp  # 把tmp归位
    return left
def _quick_sort(li, left, right):
    if left < right:  # 至少两个元素
        mid = partition(li, left, right)
        _quick_sort(li, left, mid - 1)
        _quick_sort(li, mid + 1, right)
@cal_time
def quick_sort(li):
    _quick_sort(li, 0, len(li) - 1)

li = list(range(10000, 0, -1))

快速排序的效率：

• 快速排序的时间复杂度 O(nlogn)

快速排序的问题：

• 最坏情况：如果数据本身顺序与想要的排序完全相反，每次查找的时候只归位一个数据，所以最后排序的时间复杂度是O(n**2)。解决办法：第一个要排序的数随机去获取，但是不排除每次都随机获取最大的，不过几率会很小

• 递归:python3递归最大998层，python2是999层

• # 修改递归最大成熟
  import sys
  sys.setrecursionlimit(设置上限值)