LeetCode 41-50题
本博客记录的是 LeetCode 41 到 50 题的题解
# 这样写是错误的,这个 bug 太可恶了!!
nums[i], nums[nums[i] - 1] = nums[nums[i] - 1], nums[i]
d = set()
d.add(1)
if x not in d:
return x
41. First Missing Positive
想要 O(n)的话,直接打表即可,而且我们可以优化表的大小,5*10^5
不考虑空间
自己手动打表
const int N = 5 * 1e5 + 10;
class Solution {
public:
bool st[N];
int firstMissingPositive(vector<int>& nums) {
memset(st, false, sizeof st);
int n = nums.size();
for (int i = 0; i < n; i ++ ) {
if (nums[i] <= 0 || nums[i] >= N) continue;
else st[nums[i]] = true;
}
for (int i = 1; i < N; i ++ ) {
if (st[i] == false)
return i;
}
return -1;
}
};
借助 unordered_set
const int N = 5 * 1e5 + 10;
class Solution {
public:
int firstMissingPositive(vector<int>& nums) {
unordered_set<int> hash;
for (auto x : nums) {
hash.insert(x);
}
int res = 1;
while (hash.count(res)) res ++;
return res;
}
};
python 代码自己手动 st 数组打表
class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
n = len(nums)
st = [False] * (n + 10)
for i in range(0, n):
if nums[i] <= 0 or nums[i] > (n + 2):
continue
else:
st[nums[i]] = True
for i in range(1, n + 5):
if st[i] == False:
return i
return -1
python 使用 set
class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
d, n = set(), len(nums)
for i in range(n):
d.add(nums[i])
res = 1
while (res in d):
res += 1
return res
O(n)时间,常数空间做法
该做法其实和打表 st 类似,不过他并没有申请 st 数组,而是在我们的nums 数组上进行操作,将 value[i] 放在它对应的 value[i] - 1下标的位置上,也就节省了我们的 空间
c++代码
const int N = 5 * 1e5 + 10;
class Solution {
public:
int firstMissingPositive(vector<int>& nums) {
int n = nums.size();
for (int i = 0; i < n; i ++ ) {
while ((nums[i] >= 1 && nums[i] <= n) && nums[i] != i + 1 &&
nums[nums[i] - 1] != nums[i]) {
swap(nums[i], nums[nums[i] - 1]);
}
}
for (int i = 0; i < n; i ++ ) {
if (nums[i] != i + 1) {
return i + 1;
}
}
return n + 1;
}
};
python 代码
class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
n = len(nums)
for i in range(n):
while (nums[i] > 0 and nums[i] <= n) and nums[i] != i + 1 and nums[nums[i] - 1] != nums[i]:
# print(f"i={i}, nums[i]={nums[i]}, nums[nums[i] - 1]={nums[nums[i] - 1]}")
# nums[i], nums[nums[i] - 1] = nums[nums[i] - 1], nums[i] 这样写是错误的
t = nums[nums[i] - 1]
nums[nums[i] - 1] = nums[i]
nums[i] = t
# print(nums)
for i in range(n):
if nums[i] != i + 1:
return i + 1
return n + 1
42. Trapping Rain Water
就是不断寻找区间、子区间的最大值的问题,因为可以看作是选择最大值和次最大值,中间的较小值用于盛水。
所以说我使用了线段树来写。但是速度有点略慢
线段树
const int N = 20000 * 4 + 10;
int l[N], r[N], seg_pos[N], seg_max[N];
typedef pair<int, int> PII;
class Solution {
public:
vector<int> a;
int n, res = 0;
void pushup(int u) {
if (seg_max[u * 2] > seg_max[u * 2 + 1]) {
seg_max[u] = seg_max[u * 2];
seg_pos[u] = seg_pos[u * 2];
} else {
seg_max[u] = seg_max[u * 2 + 1];
seg_pos[u] = seg_pos[u * 2 + 1];
}
}
void build(int u, int x, int y) {
if (x == y) {
l[u] = r[u] = x;
seg_max[u] = a[x];
seg_pos[u] = x;
return;
} else {
l[u] = x, r[u] = y;
int mid = (x + y) / 2;
build(u * 2, x, mid);
build(u * 2 + 1, mid + 1, y);
pushup(u);
}
}
PII query(int u, int x, int y) {
if (x == y) {
return PII(a[x], x);
}
if (l[u] > y || r[u] < x) {
return PII(-1, -1);
} else if (l[u] >= x && r[u] <= y) {
return PII(seg_max[u], seg_pos[u]);
} else {
int mid = (l[u] + r[u]) / 2;
if (mid < x) return query(u * 2 + 1, x, y);
else if (mid + 1 > y) return query(u * 2, x, y);
else {
PII t1 = query(u * 2, x, y);
PII t2 = query(u * 2 + 1, x, y);
if (t1.first > t2.first) {
return t1;
} else {
return t2;
}
}
}
}
int trap(vector<int>& height) {
// 构造线段树
a = height, n = height.size();
build(1, 0, n - 1);
// 进行答案求解
res = 0;
dfs(0, n - 1);
return res;
}
void dfs(int x, int y) {
if (abs(y - x) <= 1) {
return;
}
PII t1 = query(1, x, y), t2, t3;
int m1 = t1.first, p1 = t1.second, m2, p2, m3, p3;
if (abs(p1 - x) >= 2) {
t2 = query(1, x, p1 - 1);
m2 = t2.first, p2 = t2.second;
int tmp_ans = (p1 - p2 - 1) * m2;
for (int i = p2 + 1; i <= p1 - 1; i ++ ) {
tmp_ans -= a[i];
}
res += tmp_ans;
dfs(x, p2);
}
if (abs(y - p1) >=2) {
t3 = query(1, p1 + 1, y);
m3 = t3.first, p3 = t3.second;
int tmp_ans = m3 * (p3 - p1 - 1);
for (int i = p1 + 1; i <= p3 - 1; i ++ ) {
tmp_ans -= a[i];
}
res += tmp_ans;
dfs(p3, y);
}
}
};
单调栈
单调栈的做法,关键是在于自己画图想
c++ 代码
class Solution {
public:
typedef pair<int, int> PII;
int trap(vector<int>& height) {
stack<PII> stk;
PII tmp;
int n = height.size(), res = 0, cur_height = 0, pre_max = height[0];
for (int i = 0; i < n; i ++ ) {
if (stk.empty() || stk.top().first > height[i]) {
stk.push(PII(height[i], i));
} else {
cur_height = min(height[i], pre_max);
while (!stk.empty() && stk.top().first <= height[i]) {
tmp = stk.top(); stk.pop();
if (!stk.empty()) {
res += (cur_height - tmp.first) * (tmp.second - stk.top().second); //计算灌水的体积
}
}
stk.push(PII(height[i], i));
}
pre_max = max(pre_max, height[i]);
}
return res;
}
};
python代码
class Solution:
# 使用单调栈的写法,直接进行入栈出栈,计算水面差即可
def trap(self, a: List[int]) -> int:
res, n = 0, len(a)
stk = []
for i in range(n):
if not stk or stk[-1][0] > a[i]:
stk.append((a[i], i))
else:
cur_height = min(stk[0][0], a[i])
while stk and stk[-1][0] <= a[i]:
cur = stk.pop()
if stk:
# 水面高度差 乘以 水面宽度
res += (cur_height - cur[0]) * (cur[1] - stk[-1][1])
stk.append((a[i], i))
return res
43. Multiply Strings
就直接对应该做乘法模拟就可以了
c++ 代码使用 vector 注意清空首部 0
class Solution {
public:
string multiply(string num1, string num2) {
int n = num1.size(), m = num2.size();
vector<int> A(n), B(m), C(n + m);
for (int i = 0; i < n; i ++ ) {
A[n - i - 1] = num1[i] - '0';
}
for (int i = 0; i < m; i ++ ) {
B[m - i - 1] = num2[i] - '0';
}
for (int i = 0; i < n; i ++ ) {
for (int j = 0; j < m; j ++ ) {
C[i + j] += A[i] * B[j];
}
}
for (int i = 0; i < m + n - 1; i ++ ) {
C[i + 1] += C[i] / 10;
C[i] %= 10;
}
while (C.size() >= 2 && C.back() == 0) {
C.pop_back();
}
string res = "";
for (int i = C.size() - 1; i >= 0; i -- ) {
res += C[i] + '0';
}
return res;
}
};
应该使用 ord 函数,并且字符串翻转
class Solution:
def multiply(self, num1: str, num2: str) -> str:
n1, n2 = len(num1), len(num2)
num1 = num1[::-1]
num2 = num2[::-1]
ret = [0] * (n1 + n2 + 2)
ord_0 = ord('0')
for i in range(n1):
for j in range(n2):
ret[i + j] += (ord(num1[i]) - ord_0) * (ord(num2[j]) - ord_0)
while ret[-1] == 0 and len(ret) >= 2:
ret.pop()
t, i = 0, 0
res = ''
while t != 0 or i < len(ret):
if i < len(ret):
t += ret[i]
i += 1
res += str(t % 10)
t //= 10
return res[::-1]
44. Wildcard Matching
使用动态规划的方法完成字符串匹配问题
唯一注意地是如何优化为 O(N^2)的做法
开一个辅助数组
class Solution:
def isMatch(self, s: str, p: str) -> bool:
n, m = len(s), len(p)
f = [[False] * (m + 1) for i in range(n + 1)]
match = [[False] * (m + 1) for i in range(n + 1)]
f[0][0] = True
s = ' ' + s
p = ' ' + p
for i in range(n + 1):
match[i][0] = True
for j in range(1, m + 1):
if p[j] != '*':
break
f[0][j] = True
for i in range(1, n + 1):
for j in range(1, m + 1):
if p[j] == '*':
f[i][j] = match[i][j - 1]
else:
f[i][j] = f[i - 1][j - 1] and (s[i] == p[j] or p[j] == '?')
match[i][j] = match[i - 1][j] or f[i][j]
return f[n][m]
后来看题解,发现没必要开辅助数组,就想完全背包的优化一样,表达式就是他自己
class Solution:
def isMatch(self, s: str, p: str) -> bool:
n, m = len(s), len(p)
f = [[False] * (m + 1) for i in range(n + 1)]
s = ' ' + s
p = ' ' + p
f[0][0] = True
for i in range(1, m + 1):
if p[i] == '*':
f[0][i] = True
else:
break
for i in range(1, n + 1):
for j in range(1, m + 1):
if p[j] == '*':
f[i][j] = f[i][j - 1] or f[i - 1][j]
else:
f[i][j] = f[i - 1][j - 1] and (s[i] == p[j] or p[j] == '?')
return f[n][m]
45. Jump Game II
就一个dp,不优化的做法
class Solution:
def jump(self, nums: List[int]) -> int:
n = len(nums)
f = [10000] * (n + 1)
f[1] = 0
for i in range(1, n + 1):
for j in range(1, nums[i - 1] + 1):
if i + j > n:
break
f[i + j] = min(f[i + j], f[i] + 1)
return f[n]
思考 DP 方法如何进行优化, f[i]是走到 i 位置时所需要的倍数,
可以证明 f[i] 数组是单调不减的,也就是说 f[i] <= f[i + 1]
如果存在 f[i] > f[i + 1],那么 f[i + 1]的上一步,也一定是可达到 f[i] 的,所以说不存在 f[i] > f[i + 1] 的情况。
既然知道他是单调不减的,我们可以直接需要分界点,没必要一个一个的进行枚举,直接一个段一个段的扫描出来最范围,最后统一赋值
class Solution:
def jump(self, nums: List[int]) -> int:
n = len(nums)
f = [10000] * (n + 1)
f[0] = 0
j = 0
for i in range(n):
if i == 0 or f[i] == f[i - 1]:
j = max(j, i + nums[i])
else:
for k in range(i, min(j + 1, n)): # 注意这里要有一个 防止越界的特判
f[k] = f[i - 1] + 1
j = max(j, i + nums[i])
return f[n - 1]
46. Permutations
一个挺简单的 dfs
class Solution:
res = []
tmp_ans = []
def permute(self, nums: List[int]) -> List[List[int]]:
self.res = []
self.tmp_ans = []
st = [False] * len(nums)
self.dfs(0, len(nums), st, nums)
return self.res
def dfs(self, cur, n, st, nums):
if cur == n:
self.res.append(self.tmp_ans[:]) # 注意一定要 copy
else:
for i in range(n):
if st[i] == False:
st[i] = True
self.tmp_ans.append(nums[i])
self.dfs(cur + 1, n, st, nums)
self.tmp_ans.pop()
st[i] = False
class Solution {
public:
vector<vector<int> > res;
vector<int> tmp_res;
bool st[20];
void dfs(int cur, int n, vector<int> &nums) {
if (cur == n) {
res.push_back(tmp_res);
} else {
for (int i = 0; i < n; i ++ ) {
if (st[i] == false) {
st[i] = true;
tmp_res.push_back(nums[i]);
dfs(cur + 1, n, nums);
st[i] = false;
tmp_res.pop_back();
}
}
}
}
vector<vector<int>> permute(vector<int>& nums) {
int n = nums.size();
res.clear();
tmp_res.clear();
memset(st, false, sizeof st);
dfs(0, n, nums);
return res;
}
};
47. Permutations II
他这个不可重复的精髓在于,先将nums排序,然后对 nums[i] 的选择设置某些规则:
- 之前从未使用 st[i] == false
而且还应当满足nums[i]是第一个该数值的元素,或者是该数值前的其他元素被使用
也就是说 value 相同的数值,排序必须按照他们 idx 的顺序进行走,想要选择该元素需要让 idx 靠前 且 value 相等的 元素已经被选择
class Solution:
res = []
tmp_res = []
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
self.res = []
self.tmp_res = []
n = len(nums)
st = [False] * (n + 1)
nums.sort()
self.dfs(0, n, st, nums)
return self.res
def dfs(self, cur, n, st, nums):
if cur == n:
self.res.append(self.tmp_res[:])
else:
for i in range(n):
if st[i] == False and (i == 0 or nums[i - 1] != nums[i] or st[i - 1] == True):
self.tmp_res.append(nums[i])
st[i] = True
self.dfs(cur + 1, n, st, nums)
st[i] = False
self.tmp_res.pop()
class Solution {
public:
vector<vector<int> > res;
vector<int> tmp_res;
bool st[10];
vector<vector<int>> permuteUnique(vector<int>& nums) {
sort(nums.begin(), nums.end());
res.clear();
tmp_res.clear();
memset(st, false, sizeof st);
dfs(0, nums.size(), nums);
return res;
}
void dfs(int cur, int n, vector<int> &nums) {
if (cur == n) {
res.push_back(tmp_res);
} else {
for (int i = 0; i < n; i ++ ) {
if (st[i] == false && (i == 0 || nums[i - 1] != nums[i] || st[i - 1])) {
st[i] = true;
tmp_res.push_back(nums[i]);
dfs(cur + 1, n, nums);
tmp_res.pop_back();
st[i] = false;
}
}
}
}
};
48. Rotate Image
相似三角形直接计算旋转后的坐标
原本想用叉积,点积,以及长度相等进行计算,但是发现过于繁琐,因此这里使用了相似三角形来寻找旋转之后的坐标关系。
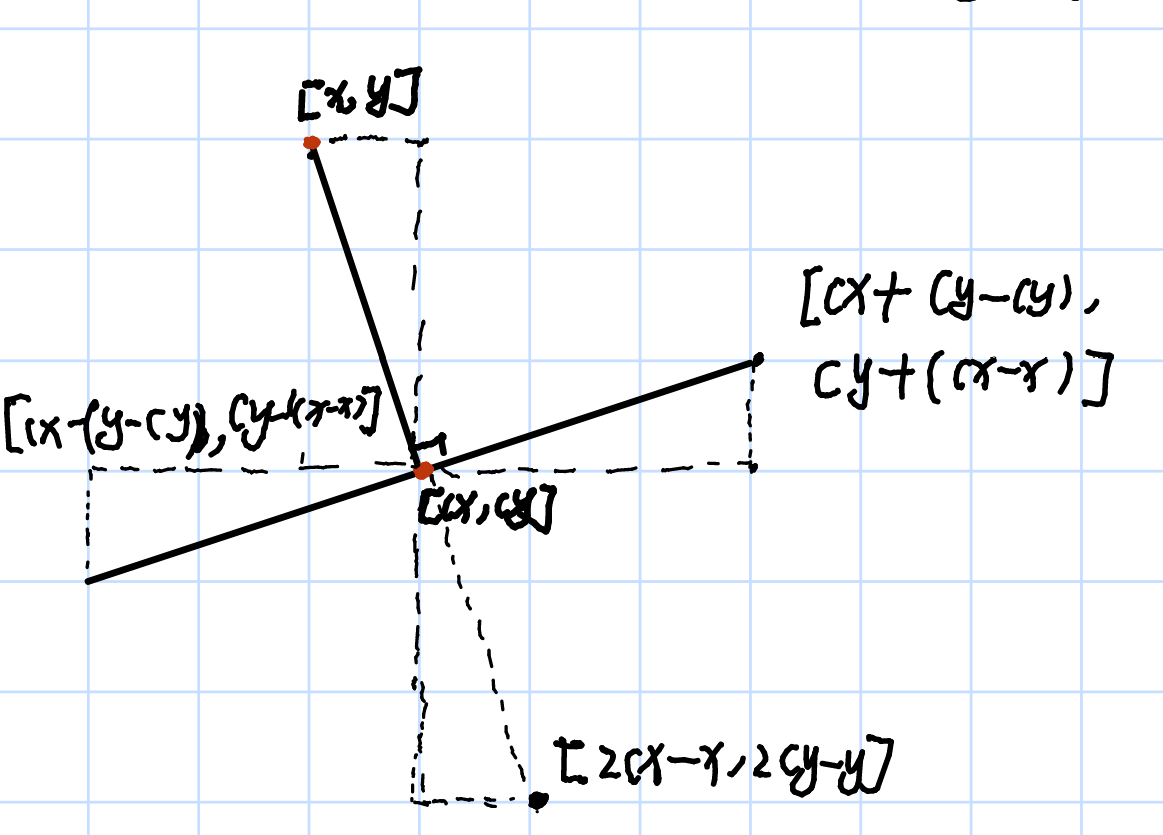
根据改坐标关系,可以不断计算出旋转之后的坐标,从而达到修改数值的目的。
C++ 代码
class Solution {
public:
int get(double x) {
return round(x);
}
void rotate(vector<vector<int>>& matrix) {
int nx, ny, px, py, t;
int n = matrix.size();
if (n & 1) { // odd
int u, v;
int cx = n / 2, cy = n / 2;
for (int x = 0; x < cx; x ++ ) {
for (int y = 0; y <= cy; y ++ ) {
u = x, v = y;
t = matrix[u][v];
for (int i = 0; i < 3; i ++ ) {
printf("i=%d, (%d, %d)\n", i, u, v);
nx = cx + cy - v, ny = cy - cx + u;
matrix[u][v] = matrix[nx][ny];
u = nx, v = ny;
}
matrix[u][v] = t;
}
}
} else { // even
double cx = (n - 1) / 2.0, cy = (n - 1) / 2.0;
double u, v;
for (int x = 0; x < cx; x ++ ) {
for (int y = 0; y < cy; y ++ ) {
u = x, v = y;
t = matrix[get(u)][get(v)];
for (int i = 0; i < 3; i ++ ) {
printf("i=%d, (%d, %d)\n", i, u, v);
nx = cx + cy - v, ny = cy - cx + u;
matrix[get(u)][get(v)] = matrix[get(nx)][get(ny)];
u = nx, v = ny;
}
matrix[u][v] = t;
}
}
}
}
};
python 代码
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
n = len(matrix)
if n % 2 == 1: # odd
cx, cy = n // 2, n // 2
for i in range(cx + 1):
for j in range(cy):
x, y = i, j
t = matrix[x][y]
for k in range(3):
nx, ny = cx + cy - y, cy - cx + x
matrix[x][y] = matrix[nx][ny]
x, y = nx, ny
matrix[x][y] = t
else: # even
cx, cy = (n - 1) / 2, (n - 1) / 2
for i in range(ceil(cx)):
for j in range(ceil(cy)):
x, y = i, j
t = matrix[x][y]
for k in range(3):
nx, ny = cx + cy - y, cy - cx + x
matrix[round(x)][round(y)] = matrix[round(nx)][round(ny)]
x, y = nx, ny
matrix[round(x)][round(y)] = t
两次对称间接寻找下一点坐标

仅给出 python 代码
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
n = len(matrix)
for i in range(0, n):
for j in range(i + 1, n):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
for i in range(n):
for j in range(ceil((n - 1) / 2)):
matrix[i][j], matrix[i][n-1-j] = matrix[i][n-1-j], matrix[i][j]
49. Group Anagrams
本题就是将字符串排序一下子,然后看排序之后的字符串是否存在(也可以不排序,排序主要是借助库函数快一些),如果不存在,那么就开一个集合,加进去,否则就放入先前已经为该类字符串整好的集合中去。
检查其是否存在方法很多,可以是 字符串 Hash,也可以是借助库函数 map<string, int> ,甚至还可以是 trie 树
借助 库函数 map
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
vector<vector<string> > res;
string t2;
unordered_map<string, int> hash;
int cnt = 0;
for (auto &t : strs) {
t2 = t;
sort(t2.begin(), t2.end());
if (hash.count(t2) == 0) {
hash[t2] = cnt ++;
res.push_back(vector<string> (0));
}
res[hash[t2]].push_back(t);
}
return res;
}
};
下面我选择字符串排序之后 Trie 树打表和直接进行 a--z的打表hash
不排序Hash
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
hash = {}
BASE, MOD = 31, int(1e9 + 7)
cnt = [0] * 31
next_idx = 0
res = []
for s in strs:
for i in range(len(cnt)):
cnt[i] = 0
for ch in s:
cnt[ord(ch) - ord('a')] += 1
num = 0
for i in range(26):
num = (num * BASE + cnt[i]) % MOD # 在这里对 26 个cnt 进行 hash
if num not in hash:
hash[num] = next_idx
next_idx += 1
res.append([])
res[hash[num]].append(s)
return res
trie树
对处理好的 cnt 数组进行 Trie 串联,查找它对应的 idx 下标
class Trie_node:
idx = -1
son = {}
def __init__(self):
self.idx = -1
self.son = {} # 一定要注意初始化
class Solution:
next_idx = 0
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
def search(cur_node, cur, n, cnt):
if cur == n:
return cur_node.idx
elif cnt[cur] in cur_node.son:
return search(cur_node.son[cnt[cur]], cur + 1, n, cnt)
else:
return -1
def insert(cur_node, cur, n, cnt):
if cur == n:
cur_node.idx = self.next_idx
self.next_idx += 1
return cur_node.idx
else:
if cnt[cur] in cur_node.son:
return insert(cur_node.son[cnt[cur]], cur + 1, n, cnt)
else:
cur_node.son[cnt[cur]] = Trie_node()
return insert(cur_node.son[cnt[cur]], cur + 1, n, cnt)
BASE, MOD = 31, int(1e9 + 7)
cnt = [0] * 31
res = []
base_trie = Trie_node()
for s in strs:
for i in range(len(cnt)):
cnt[i] = 0
for ch in s:
cnt[ord(ch) - ord('a')] += 1
idx = search(base_trie, 0, 26, cnt)
if idx == -1:
idx = insert(base_trie, 0, 26, cnt)
res.append([])
res[idx].append(s)
return res
50. Pow(x, n)
就是一个简单的快速幂,甚至都不用去模了。。。
class Solution:
def myPow(self, base: float, n: int) -> float:
res = 1.0
is_negative = True if n < 0 else False
n = abs(n)
while n:
if n % 2 == 1:
res *= base
n //= 2
base *= base
return (res if not is_negative else 1.0 / res)
C++ 代码
class Solution {
public:
double myPow(double x, int n) {
double res = 1.0;
bool is_negative = (n < 0);
n = abs(n);
while (n) {
if (n & 1) {
res *= x;
}
x *= x;
n /= 2;
}
if (is_negative) {
return 1.0 / res;
} else {
return res;
}
}
};



 浙公网安备 33010602011771号
浙公网安备 33010602011771号