Varibad:A very good method for bayes-adaptive deep rl via meta-learning
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

Published as a conference paper at ICLR 2020
ABSTRACT
在未知环境中权衡探索和开发是在学习过程中实现期望回报最大化的关键。贝叶斯最优策略不仅以环境状态为条件,而且以智能体对环境的不确定性为条件。然而,计算贝叶斯最优策略对于除最小任务外的所有任务来说都是棘手的。在本文中,我们引入了变分贝叶斯自适应深度RL(variBAD),这是一种在未知环境中进行近似推理的元学习方法,并在动作选择过程中直接引入任务的不确定性。在网格世界领域中,我们展示了variBAD如何作为任务不确定性的函数执行结构化在线探索。我们进一步评估了元RL中广泛使用的MuJoCo域上的variBAD,并表明它比现有方法获得了更高的在线回报。
1 INTRODUCTION
强化学习(RL)通常涉及为具有未知奖励和转移函数的给定马尔可夫决策过程(MDP)找到最大化期望回报的最优策略。如果知道这些,理论上可以在没有环境相互作用的情况下计算最优策略。相比之下,在未知环境中学习通常需要权衡探索(了解环境)和开发(采取有希望的动作)。平衡这种权衡是最大化学习期间期望回报的关键,这在许多情况下都是可取的,尤其是在医疗和教育等高风险的现实世界应用中(Liu et al.,2014;Yauney & Shah,2018)。贝叶斯最优策略以最优方式进行这种权衡,它不仅对环境状态,而且对智能体自身对当前MDP的不确定性进行操作。
原则上,可以使用贝叶斯自适应马尔可夫决策过程(BAMDP)的框架来计算贝叶斯最优策略(Martin,1967;Duff & Barto,2002),其中智能体在可能的环境中保持置信分布。用这种信念扩充底层MDP的状态空间会产生BAMDP,这是信念MDP的一种特殊情况(Kaelbling et al.,1998)。贝叶斯最优智能体通过系统地寻找快速减少不确定性所需的数据来最大化BAMDP中的期望回报,但前提是这样做有助于最大化期望回报。其性能受给定MDP的最优策略的约束,该策略不需要采取探索性动作,但需要有关MDP的先验知识来计算。
不幸的是,BAMDP中的规划,即计算以增强状态为条件的贝叶斯最优策略,对于除最小任务外的所有任务来说都是棘手的。一个常见的捷径是依赖后验采样(Thompson,1933;Strens,2000;Osband et al.,2013)。这里,智能体从其后验中周期性地对单个假设MDP进行采样(例如,在事件开始时),并且遵循对采样的MDP最优的策略,直到提取下一个样本。规划要容易得多,因为它是在常规MDP上完成的,而不是BAMDP。然而,后验采样的探索可能效率很低,而且远不是贝叶斯最优的。
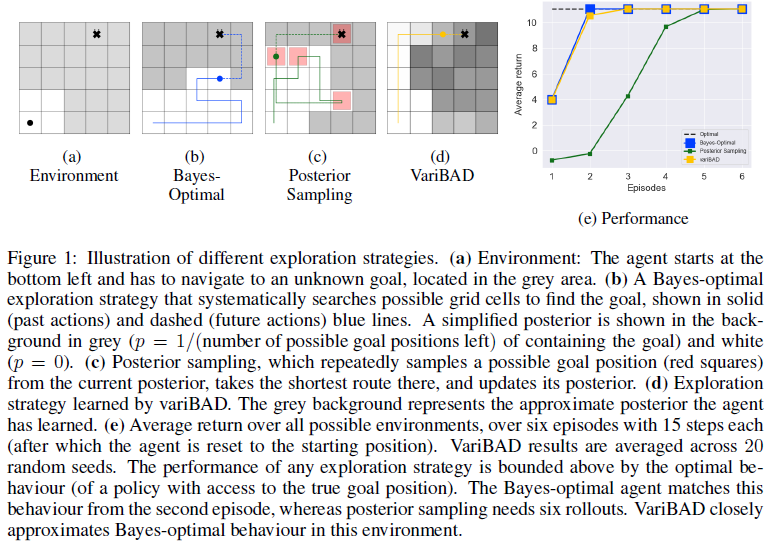
考虑图1中的网格世界示例,其中智能体必须导航到灰色区域中的未知目标(1a)。为了保持后验性,智能体可以将非零概率均匀地分配给目标所在的细胞,并将零概率均匀分配给所有其他细胞。贝叶斯最优策略从战略上搜索后验认为可能的目标位置集,直到找到目标(1b)。通过对比的后验采样对可能的目标位置进行采样,在那里采取最短的路线,然后对与更新后验不同的目标位置重新采样(1c)。这样做的效率要低得多,因为智能体的不确定性没有以最优方式降低(例如,状态被重新访问)。
正如这个例子所示,贝叶斯最优策略可以比后验采样更有效地探索。一个关键的挑战是学习近似贝叶斯最优策略,同时保持后验采样的易处理性。此外,即使是后验采样也需要维持后验信念的推理,这本身可能是难以解决的。
在本文中,我们结合了贝叶斯RL、近似变分推理和元学习的思想来应对这些挑战,并使智能体能够战略性地探索给定分布的看不见(但相关)环境,以最大限度地提高其期望在线回报。
更具体地说,我们提出了变分贝叶斯自适应深度RL(variBAD),这是一种元学习的方法,可以对未知任务进行近似推理1,并在动作选择过程中直接引入任务的不确定性。给定MDP p(M)上的分布,我们使用学到的低维随机潜变量m和联合元训练来表示单个MDP M:
- 一种变分自编码器,在与环境交互时,根据智能体的经验,可以推断新任务中m上的后验分布,以及
- 一种以这种对MDP嵌入的后验信念为条件的策略,从而学会在任务不确定性下选择动作时如何权衡探索和开发。
图1e显示了我们的方法相对于硬编码最优(具有特权目标信息)、贝叶斯最优和后验采样探索策略的性能。variBAD的性能与贝叶斯最优性能非常匹配,与第三次rollout时的最优性能相匹配。
以前的BAMDP方法只能在具有小动作和状态空间的环境中处理,或者在训练期间依赖于有关任务的特权信息。variBAD提供了一种易于处理和灵活的方法来学习针对训练任务分布的贝叶斯自适应策略,唯一的假设是这种分布可用于元训练。我们在上面显示的网格世界和在元RL中广泛使用的MuJoCo域上评估了我们的方法,并表明与现有的元学习方法相比,variBAD在测试时表现出更好的探索行为,在学习过程中获得了更高的回报。因此,variBAD为深度强化学习开辟了一条易于处理的近似贝叶斯最优探索之路。
1 我们可以互换使用术语“环境”、“任务”和“MDP”。
2 BACKGROUND
我们将马尔可夫决策过程(MDP)定义为元组M = (S, A, R, T, T0, γ, H),其中S是一组状态,A是一组动作,R(rt+1|st, at, st+1)是奖励函数,T(st+1|st, at)是转移函数,T0(s0)是初始状态分布,γ是折扣因子,H是眼界。在标准RL设置中,我们希望学习一种最大化的策略π,期望回报。在这里,我们考虑一个多任务元学习设置,我们接下来将介绍它。
2.1 TRAINING SETUP
我们采用标准元学习设置,其中我们在MDP上具有分布p(M),我们可以在元训练期间从中采样,其中MDP Mi ~ p(M)由元组Mi = (S, A, Ri, Ti, Ti,0, γ, H)定义。在不同的任务中,奖励和转换函数各不相同,但有一些共同的结构。索引 i 表示未知的任务描述(例如,目标位置或自然语言指令)或任务ID。从p(M)采样MDP通常通过从分布p(R, T)采样奖励和转换函数来完成。在元训练过程中,对一批任务进行重复采样,并对每一批任务执行一个小的训练过程,目的是学会学习(有关现有方法的概述,请参见第4节)。在元测试时,对于从p中提取的任务,基于它在学习过程中获得的平均回报来评估智能体。要做好这一点至少需要两件事:(1)结合在相关任务中获得的先验知识,以及(2)在选择动作以权衡探索和开发时对任务的不确定性进行推理。在下文中,我们结合了元学习和贝叶斯RL的思想来应对这些挑战。
2.2 BAYESIAN REINFORCEMENT LEARNING
当MDP未知时,在选择动作时,最优决策必须权衡探索和开发。原则上,这可以通过采用贝叶斯方法进行强化学习来实现,该方法被形式化为贝叶斯自适应MDP(BAMDP),其解决方案是贝叶斯最优策略(Bellman,1956;Duff & Barto,2002;Ghavamzadeh et al.,2015)。
在RL的贝叶斯公式中,我们假设转移和奖励函数是根据先验b0 = p(R, T)分布的。由于智能体无法访问真正的奖励和转换函数,因此它可以保持信念bt(R, T) = p(R, T|τ:t),这是给定智能体经验的MDP的后验τ:t = {s0, a0, r1, s1, a1, ... , st}直到当前时间步骤。这通常是通过保持模型参数的分布来实现的。
为了允许智能体将任务的不确定性纳入其决策中,可以将这种信念扩展到状态,从而产生超状态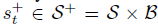 ,其中B是信念空间。这些转换根据
,其中B是信念空间。这些转换根据
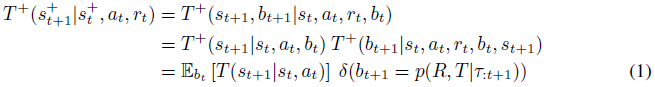
即,新环境状态st是关于转换函数的当前后验分布的期望新状态,并且根据贝叶斯规则确定地更新置信度。超状态上的奖励函数被定义为当前后验(在状态转换之后)超奖励函数下的期望奖励,
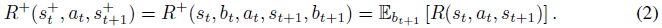
这导致了BAMDP ![]() (Duff & Barto,2002),这是信念MDP的一个特例,即通过在部分可观察的MDP中取智能体保持的后验信念并将其重新解释为马尔可夫状态而形成的MDP(Cassandra et al.,1994)。在一个任意的信念MDP中,信念是一个隐藏的状态,它可以随着时间的推移而改变。在BAMDP中,信念是关于转换和奖励函数的,这对于给定的任务是恒定的。智能体现在的目标是最大限度地提高BAMDP的期望回报,
(Duff & Barto,2002),这是信念MDP的一个特例,即通过在部分可观察的MDP中取智能体保持的后验信念并将其重新解释为马尔可夫状态而形成的MDP(Cassandra et al.,1994)。在一个任意的信念MDP中,信念是一个隐藏的状态,它可以随着时间的推移而改变。在BAMDP中,信念是关于转换和奖励函数的,这对于给定的任务是恒定的。智能体现在的目标是最大限度地提高BAMDP的期望回报,
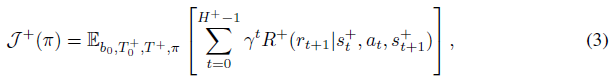
即,在最初未知的环境中最大化期望回报,同时在视界H+内学习。注意MDP视界H和BAMDP视界H+之间的区别。尽管它们经常重合,但我们可能希望智能体在前N个MDP事件中表现出贝叶斯最优,因此H+ = N×H。最优的探索和开发权衡在很大程度上取决于智能体还剩多少时间(例如,决定信息寻求动作是否值得)。
(3)中的目标通过贝叶斯最优策略最大化,该策略自动权衡探索和开发:只有在有助于最大限度地提高视界内的期望回报,它才会采取探索动作来减少任务的不确定性。BAMDP框架之所以强大,是因为它提供了一种制定贝叶斯最优行为的原则性方法。然而,对于大多数有趣的问题来说,解决BAMDP是令人绝望的棘手问题。
主要挑战如下。
- 我们通常不知道真正的奖励和/或转换模型的参数化,
- 置信度更新(计算后验p(R,T|τ:t))通常是棘手的,并且
- 即使有正确的后验,在信念空间中的规划通常也是棘手的。
在下文中,我们提出了一种同时元学习奖励和转换函数的方法,如何在未知MDP中进行推理,以及如何使用信念来最大化期望在线回报。由于贝叶斯自适应策略是通过推理框架端到端学习的,因此在测试时不需要规划。我们做出了最小的假设(在训练过程中不需要特权任务信息),从而为贝叶斯自适应深度RL提供了一种高度灵活且可扩展的方法。
3 BAYES-ADAPTIVE DEEP RL VIA META-LEARNING
在本节中,我们将介绍variBAD,并描述我们如何应对上述挑战。我们首先描述如何表示奖励和转换函数,以及这些函数的(后验)分布。然后,我们考虑如何在给定的任务中进行元学习来执行近似变分推理,并最终将所有部分放在一起形成我们的训练目标。
在典型的元学习环境中,每个MDP唯一的奖励和转换函数是未知的,但在p(M)中的MDP Mi之间也共享一些结构。我们知道存在一个表示任务描述或任务ID的真 i,但我们无法访问这些信息。因此,我们使用学到的随机潜变量mi来表示这个值。对于给定的MDP Mi,我们可以写
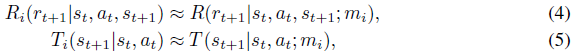
其中R和T在任务之间共享。由于我们无法访问真实的任务描述或ID,我们需要在Mi中收集的智能体到时间步骤 t 的经验的情况下推断mi,
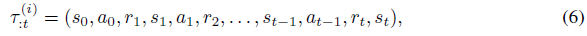
即,我们想推断给定![]() 的mi上的后验分布
的mi上的后验分布![]() (从现在起,为了便于记法,我们去掉下标 i)。
(从现在起,为了便于记法,我们去掉下标 i)。
回想一下,我们的目标是学习MDP上的分布,并在给定环境的后验知识的情况下计算最优动作。考虑到上面的重新表述,现在就足以推理嵌入m,而不是转换和奖励动态。这在部署深度学习策略时尤其有用,其中奖励和转换函数可以由数百万个参数组成,但嵌入m可以是一个小向量。
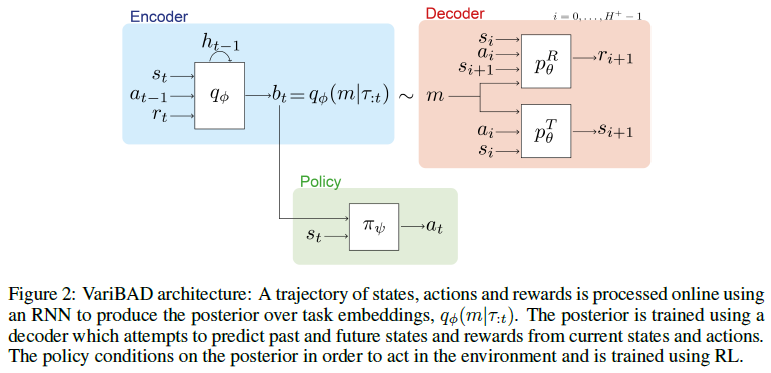
3.1 APPROXIMATE INFERENCE
计算精确的后验通常是不可能的:我们无法访问MDP(因此也无法访问转换和奖励函数),并且在任务上边缘化在计算上是不可行的。因此,我们需要学习环境的模型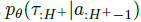 (参数化为θ)与摊销推理网络
(参数化为θ)与摊销推理网络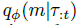 (参数化为Φ),允许在每个时间步骤 t 的运行时进行快速推理。动作选择策略不是MDP的一部分,因此环境模型只能在以动作为条件时产生轨迹分布,我们通常从当前策略a ~ π中得出这一点。因此,在任何给定的时间步骤 t,我们的模型学习目标都是最大化
(参数化为Φ),允许在每个时间步骤 t 的运行时进行快速推理。动作选择策略不是MDP的一部分,因此环境模型只能在以动作为条件时产生轨迹分布,我们通常从当前策略a ~ π中得出这一点。因此,在任何给定的时间步骤 t,我们的模型学习目标都是最大化
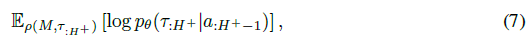
其中![]() 是由我们的策略引起的轨迹分布,我们通过用 τ 状态奖励轨迹来表示,不包括动作,从而稍微滥用了符号。在下文中,我们放弃对a:H+-1的条件以简化记法。
是由我们的策略引起的轨迹分布,我们通过用 τ 状态奖励轨迹来表示,不包括动作,从而稍微滥用了符号。在下文中,我们放弃对a:H+-1的条件以简化记法。
我们可以优化一个可处理的下界,而不是优化(7),该下界由学到的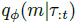 近似后验定义,可以通过蒙特卡洛采样估计(完整推导见附录A):
近似后验定义,可以通过蒙特卡洛采样估计(完整推导见附录A):
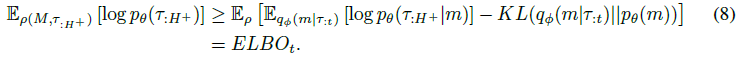
![]() 项通常被称为重建损失,
项通常被称为重建损失,![]() 被称为解码器。
被称为解码器。![]() 项是我们的变分后验qΦ和嵌入pθ(m)上的先验之间的KL散度。我们将先验设置为先前的后验,
项是我们的变分后验qΦ和嵌入pθ(m)上的先验之间的KL散度。我们将先验设置为先前的后验,![]() ,其中初始先验
,其中初始先验![]() 。
。
从公式(8)和图2中可以看出,当智能体处于时间步骤 t 时,我们对过去的轨迹τ:t进行编码,以获得当前的后验q(m|τ:t),因为这是可用于执行关于当前任务的推断的所有信息。然后,我们解码整个轨迹:τ:H+,包括未来,即模型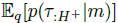 。这与传统的VAE设置不同(这是可能的,因为我们在训练期间可以访问这些信息)。解码过去和未来都很重要,因为通过这种方式,variBAD学会对给定过去的看不见的状态进行推理。
。这与传统的VAE设置不同(这是可能的,因为我们在训练期间可以访问这些信息)。解码过去和未来都很重要,因为通过这种方式,variBAD学会对给定过去的看不见的状态进行推理。
重建项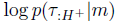 分解为
分解为
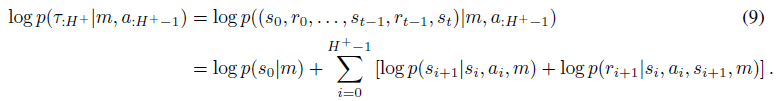
这里,p(s0|m)是初始状态分布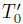 ,p(si+1|si, ai; m)是转换函数T',p(ri+1|st, at, si+1, m)为奖励函数R'。从现在开始,为了便于记法,我们将
,p(si+1|si, ai; m)是转换函数T',p(ri+1|st, at, si+1, m)为奖励函数R'。从现在开始,为了便于记法,我们将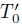 包含在T'中。
包含在T'中。
3.2 TRAINING OBJECTIVE
我们现在可以制定一个训练目标,用于学习任务嵌入、策略以及广义奖励和转换函数R'和T'的近似后验分布。我们使用深度神经网络来表示各个组件。这些是:
- 编码器qΦ(m|τ:t),参数化为Φ;
- 近似转换函数
![]() 和近似奖励函数
和近似奖励函数![]() ,它们共同被参数化为θ;和
,它们共同被参数化为θ;和 - 由Ψ参数化并依赖于Φ的策略
![]() 。
。
该策略以环境状态和m上的后验为条件,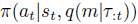 。这类似于2.2中引入的BAMDP的公式,不同之处在于我们学习了MDP嵌入上的统一分布,而不是直接学习转换/奖励函数。这使得学习更容易,因为需要进行推理的参数更少,而且我们可以使用所有任务的数据来学习共享的奖励和转换函数。后验可以由分布的参数表示(例如,如果q是高斯的,则为均值和标准差)。
。这类似于2.2中引入的BAMDP的公式,不同之处在于我们学习了MDP嵌入上的统一分布,而不是直接学习转换/奖励函数。这使得学习更容易,因为需要进行推理的参数更少,而且我们可以使用所有任务的数据来学习共享的奖励和转换函数。后验可以由分布的参数表示(例如,如果q是高斯的,则为均值和标准差)。
我们的总体目标是最大限度地
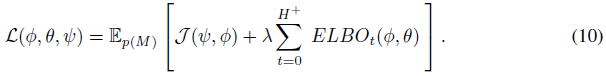
期望值通过蒙特卡洛样本近似,ELBO可以使用重参数化技巧进行优化(Kingma & Welling, 2014)。对于t = 0,我们使用先验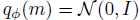 。我们使用循环网络对过去的轨迹进行编码,如Duan等人(2016); Wang等人(2016),但可以考虑其他类型的编码器,如Zaheer等人(2017); Garnello等人(2018); Rakelly等人(2019)使用的编码器。网络架构如图2所示。
。我们使用循环网络对过去的轨迹进行编码,如Duan等人(2016); Wang等人(2016),但可以考虑其他类型的编码器,如Zaheer等人(2017); Garnello等人(2018); Rakelly等人(2019)使用的编码器。网络架构如图2所示。
在公式(10)中,我们看到ELBO出现在所有可能的上下文长度 t 上。这样,variBAD可以学习如何在线执行推理(当智能体与环境交互时),并在给定更多数据的情况下随着时间的推移降低其不确定性。在实践中,如果H+很大,为了计算效率,我们可以对固定数量的ELBO项(对于随机时间步骤 t)进行二次采样。
对公式(10)进行端到端训练,并根据RL损失对监督模型学习目标进行加权。这是必要的,因为参数是在模型和策略之间共享的。然而,我们发现,在实践中,通过编码器反向传播RL损失通常是不必要的。不这样做也大大加快了训练速度,避免了权衡这些损失的需要,并防止了对方损失梯度之间的干扰。因此,在我们的实验中,我们使用不同的优化器和学习率来优化策略和VAE。我们使用不同的数据缓冲区来训练RL智能体和VAE:由于我们在实验中使用了策略算法,因此只使用最新的数据来训练策略;对于VAE,我们保留了一个单独且更大的观测轨迹缓冲区。
在元测试时,我们在随机采样的测试任务中推出策略(通过编码器和策略的前向传递),以评估性能。在测试时不使用解码器,也不进行梯度自适应:该策略已经学会在元训练期间近似贝叶斯最优。
4 RELATED WORK
Meta Reinforcement Learning. 一种突出的无模型元RL方法是利用循环网络的动力学进行快速自适应(RL2,Wang等人(2016);Duan等人(2016))。在每一个时间步骤,网络都会得到一个由前继动作和奖励组成的辅助。这使得一个任务中的学习可以在线进行,完全在循环网络的动态中进行。如果我们移除解码器(图2)和VAE目标(公式(7)),则variBAD减少到该设置,即主要区别在于,我们使用随机潜在变量(表示不确定性的归纳偏差)和解码器来重建先前和未来的转换/奖励(这是一种辅助损失(Jaderberg et al.,2017),以在潜在空间中对任务进行编码,并推导出关于看不见状态的信息)。Ortega等人(2019)对元学习顺序策略以及如何在贝叶斯框架内重塑基于记忆的元学习进行了深入讨论。
元RL的另一种流行方法是学习模型的初始化,这样在测试时,只需要几个梯度步骤就可以获得良好的性能(Finn et al.,2017;Nichol & Schulman,2018)。这些方法并不能直接解释初始策略需要探索的事实,Stadie等人(2018)(E-AML)和Rothfuss等人(2019)(ProMP)也解决了这一问题。就模型复杂性而言,MAML和ProMP相对较轻,因为它们通常由前馈策略组成。RL2和variBAD使用循环模块,这增加了模型的复杂性,但允许在线自适应。在测试时执行梯度自适应的其他方法是,例如,Houthooft等人(2018)元学习以测试时使用的智能体经验为条件的损失函数,从而学习策略(从头开始);以及Sung等人(2017),他们学习了一种元评论家,可以针对任何任务评判任何参与者,并在测试时用于训练策略。与variBAD相比,这些方法通常在测试时通过设计将探索(梯度适应之前)和开发(梯度适应之后)分开,这使得它们的样本效率较低。
Skill / Task Embeddings. 元/迁移强化学习的学习(变分)任务或技能嵌入被用于各种方法。Hausman等人(2018)使用近似变分推理学习技能的嵌入空间(具有与variBAD不同的下界)。在测试时,策略是固定的,并且学习一个新的嵌入器,在已经学习的技能之间进行插值。Arneqvist等人(2019)学习了针对不同技能的最优Q函数的随机嵌入,并将策略设置在该嵌入的(样本)上。测试时的适应是在潜在空间中进行的。Co-Reyes等人(2018)学习了一个可以由更高级别的策略控制的低级别技能的潜在空间,该策略是在分层RL的背景下制定的。这种嵌入是使用VAE来编码状态轨迹并解码状态和动作来学习的。Zintgraf等人(2019)学习了类似于MAML训练的确定性任务嵌入(Finn et al.,2017)。与variBAD类似,Zhang等人(2018)使用学到的动力学和奖励模块来学习策略所依赖的潜在表示,并表明将(固定)编码器转移到新环境有助于学习。Perez等人(2018)学习具有辅助潜变量的动态模型,并将其用于模型预测控制。Lan等人(2019)使用类似于MAML的优化程序学习任务嵌入,其中编码器在测试时更新,并且策略是固定的。Sæmundsson等人(2018)明确学习了环境模型的嵌入,随后将其用于模型预测控制(而不是像variBAD中那样用于探索)。在模仿学习领域,一些方法嵌入专家演示来表示任务;例如,Wang等人(2017)使用变分方法,Duan等人(2017)学习确定性嵌入。
variBAD与上述方法的不同之处主要在于嵌入代表什么(即任务不确定性)以及如何使用:MDP上后验分布的策略条件,使其能够推理任务的不确定性,并在网上权衡探索和开发。我们的目标(8)明确优化贝叶斯最优行为。与上面的一些方法不同,我们在测试时不使用模型,但基于模型的规划是未来工作的自然扩展。
Bayesian Reinforcement Learning. RL的贝叶斯方法可用于量化不确定性,以支持动作选择,并提供一种将先验知识纳入算法的方法(见Ghavamzadeh等人(2015)的综述)。贝叶斯最优策略是一种在探索和开发之间进行最优权衡的策略,从而使学习过程中的期望回报最大化。虽然这种策略原则上可以使用BAMDP框架进行计算,但对于除最小任务外的所有任务来说,它都是难以解决的。因此,现有的方法仅限于小型离散状态/动作空间(Asmuth & Littman,2011;Guez et al.,2012;2013),或一组离散的任务(Brunskill,2012;Poupart et al.,2006)。variBAD通过利用元学习和近似变分推理的思想,为深度RL的可处理的近似贝叶斯最优探索开辟了一条道路,唯一的假设是我们可以在一组相关任务上进行元训练。现有的近似贝叶斯RL方法通常需要我们定义奖励/转换函数的先验/信念更新,并依赖于(可能昂贵的)基于样本的规划程序。然而,由于使用了深度神经网络,variBAD缺乏上述一些方法所享有的形式保证。
与我们的方法密切相关的是Humplik等人(2019)最近的工作。与variBAD一样,它们将策略设置在MDP上的后验分布上,MDP是使用特权信息(如任务描述)进行元训练的。相比之下,variBAD元学习以无监督的方式表示信念,并且在训练过程中不依赖于特权任务信息。
后验采样(Strens,2000;Osband et al.,2013)将Thompson采样(Thompson,1933)从赌博机扩展到MDP,估计了MDP的后验分布(即模型和奖励函数),与variBAD的精神相同。该后验用于周期性地对单个假设MDP进行采样(例如,在事件开始时),随后遵循对采样的MDP最优的策略。这种方法的效率低于贝叶斯最优行为,因此在学习过程中通常具有较低的期望回报。
抽象知识的任务间转移的一种相关方法是将具有先验的策略搜索作为马尔可夫链蒙特卡罗推理(Wingate et al.,2011)。类似地,Guez等人(2013)提出了一种基于蒙特卡洛树搜索的贝叶斯规划方法,以获得一种易于处理的、基于样本的方法来获得近似贝叶斯最优行为。Osband等人(2018)指出,决策的非贝叶斯处理可能是任意次优的,并提出了一种简单的基于随机先验的结构化探索方法。最近的一些深层RL方法使用随机潜变量进行结构化探索(Gupta et al.,2018;Rakelly et al.,2019),这产生了类似于后验采样的行为。使用后验方法进行探索的其他方法是,例如,某些奖励奖金Kolter & Ng (2009); Sorg等人(2012)和基于面对不确定性时的乐观主义的方法(Kearns & Singh,2002;Brafman & Tennenholtz,2002)。在实践中经常使用非贝叶斯方法进行探索,例如其他探索奖励(例如,通过状态访问计数)或使用不知情的动作采样(例如,ε-贪婪的动作选择)。这种方法容易造成浪费性的探索,无助于最大限度地提高期望奖励。
与BAMDP相关的是上下文MDP,其中任务描述被称为上下文,环境动态和奖励取决于上下文(Hallak et al.,2015;Jiang et al.,2017;Dann et al.,2018;Modi & Tewari,2019)。这一领域的研究通常涉及通过对上下文进行假设来发展严格的界限,例如已知的上下文数量很少,或者上下文与动态/奖励之间存在线性关系。类似地,隐藏参数(HiP-)MDP的框架假设存在一组低维潜在因素,这些因素定义了一系列相关的动力系统(具有共享的奖励结构),类似于我们在公式(5)中做出的假设(Doshi-Velez & Konidaris,2016;Killian et al.,2017;Yao et al.,2018)。然而,这些方法并不直接学习贝叶斯最优行为,而是允许在新环境中有更长的训练期来推断延迟并训练策略。
Variational Inference and Meta-Learning. variBAD与许多现有的贝叶斯RL方法的主要区别在于,我们元学习推理过程,即如何进行后验更新。除了上述(RL)方法外,在Garnello等人(2018); Gordon等人(2019); Choi等人(2019)中也可以找到该方向的相关工作。相比之下,variBAD有一个针对贝叶斯最优RL设置的推理过程。
POMDPs. 最近,在部分可观测的马尔可夫决策过程中,提出了几种用于无模型强化学习(Igl et al.,2019)和用于规划的模型学习(Tschiatschek et al.,2018)的深度学习方法,并利用近似变分推理方法。相比之下,variBAD专注于BAMDP(Martin,1967;Duff & Barto,2002;Ghavamzadeh et al.,2015),这是POMDP的一个特例,其中转换和奖励函数构成了隐藏状态,智能体必须对它们保持信念。虽然POMDP中的隐藏状态通常会在每个时间步骤发生变化,但在BAMDP中,底层任务以及隐藏状态是固定的。我们通过学习随时间固定的嵌入来利用这一特性,而不像Igl等人(2019)那样使用过滤来跟踪不断变化的隐藏状态。虽然我们利用了深度近似变分推理的能力,但BAMDP的其他方法通常使用更准确但可扩展性较差的方法,例如Lee等人(2019)离散潜在分布,并使用贝叶斯滤波进行后验更新。
5 EXPERIMENTS
在本节中,我们首先研究了variBAD在教学网格世界域上的性质。我们展示了variBAD在推断手头任务时执行结构化和在线探索。然后,我们通过在元RL文献中常用的四个MuJoCo连续控制任务上使用来考虑更复杂的元学习设置。我们表明,与许多现有的元学习方法不同,variBAD在第一次推出时学会了适应任务。详细信息和超参数可在附录中找到https://github.com/lmzintgraf/varibad.
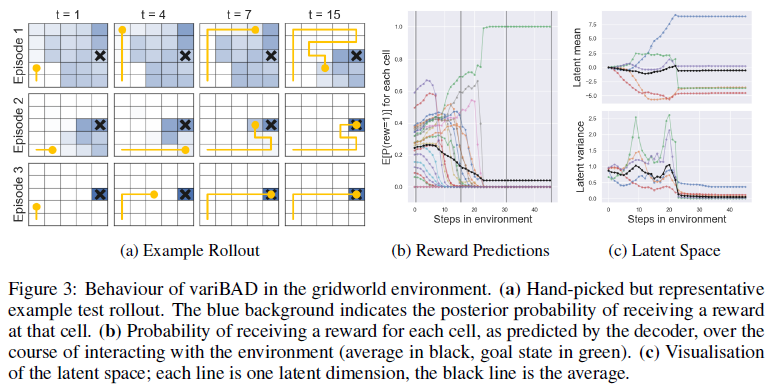
5.1 GRIDWORLD
5.2 MUJOCO CONTINUOUS CONTROL META-LEARNING TASKS
6 CONCLUSION & FUTURE WORK
我们提出了一种新的深度RL方法varyBAD来近似贝叶斯最优行为,该方法使用元学习来利用在相关任务中获得的知识,并在未知环境中进行近似推理。在说教式的网格世界环境中,我们的代理与贝叶斯最优行为密切匹配,在更具挑战性的MuJoCo任务中,variBAD在单集内获得的奖励方面优于现有方法。总之,我们相信variBAD为深度强化学习的可处理近似贝叶斯最优探索开辟了一条道路。
基于variBAD的未来工作有几个有趣的方向。例如,我们目前在测试时不使用解码器。取而代之的是,可以使用解码器进行模型预测规划,或者了解预测的错误程度(这可能表明我们没有分布,需要进一步的训练)。未来研究的另一个令人兴奋的方向是考虑环境的训练和测试分布不相同的环境。对分布外任务的泛化带来了额外的挑战,特别是对于variBAD,可能会出现两个问题:推理过程将是错误的(先验和/或后验更新),并且策略将无法解释更改的后验。在这种情况下,编码器/解码器的进一步训练可能是必要的,同时更新策略和/或明确规划。
Supplementary Material
A FULL ELBO DERIVATION
B EXPERIMENTS: GRIDWORLD
B.1 ADDITIONAL REMARKS
B.2 HYPERPARAMETERS
B.3 COMPARISON TO RL2
C EXPERIMENTS: MUJOCO
C.1 LEARNING CURVES
C.2 TRAINING DETAILS AND COMPARISON TO RL2
C.3 CHEETAHDIR TEST TIME BEHAVIOUR
C.4 RUNTIME COMPARISON
C.5 LATENT SPACE VISUALISATION
C.6 HYPERPARAMETERS


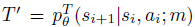 和近似奖励函数
和近似奖励函数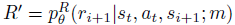 ,它们共同被参数化为θ;和
,它们共同被参数化为θ;和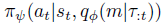 。
。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号