Short-Term Plasticity Neurons Learning to Learn and Forget
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

Proceedings of the 39th International Conference on Machine Learning, 2022
Abstract
短期可塑性(STP)是一种将衰退记忆储存在大脑皮层突触中的机制。在计算实践中,STP已经被使用,但主要用于脉冲神经元,尽管理论预测它是某些动态任务的最佳解决方案。在这里,我们提出了一种新型的循环神经单元,STP神经元(STPN),它确实非常强大。其关键机制是突触具有一种状态,通过突触内的自循环连接随时间传播。这种公式能够通过时序反向传播来训练可塑性,从而在短期内形成一种学习和遗忘的形式。STPN优于所有测试的替代方案,即RNN、LSTM以及其他具有快速权重和可微可塑性的模型。我们在监督和强化学习(RL)以及联想检索、迷宫探索、Atari视频游戏和MuJoCo机器人等任务中都证实了这一点。此外,我们计算出,在神经形态或生物回路中,STPN使模型之间的能量消耗最小化,因为它动态地抑制单个突触。基于这些,生物STP可能是一个强大的进化吸引子,可以最大限度地提高效率和计算能力。STPN现在也将这些神经形态优势带到了广泛的机器学习实践中。代码可在https://github.com/NeuromorphicComputing/stpn中获取。
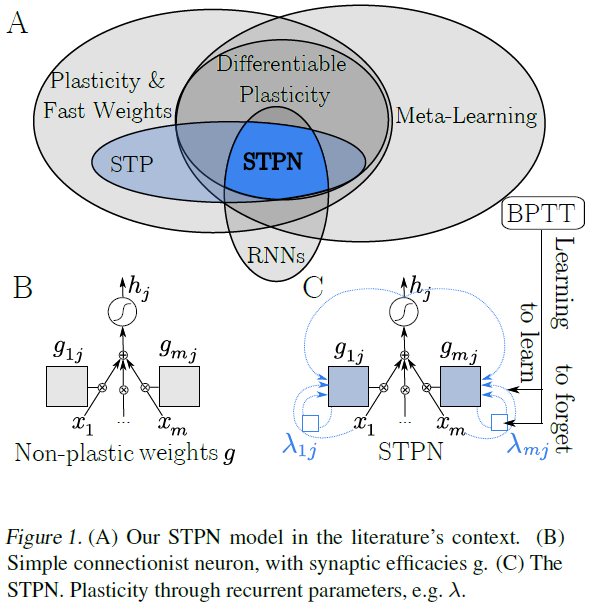
1. Introduction
1.1. Biological vs artificial neural networks
1.2. Neuromorphic Computing
1.3. Plasticity and Short-Term Plasticity
1.4. Learning to learn
1.5. Contribution to the field
我们提出了STPN,这是一种新的循环型单位,它扩展了RNN家族,在每个输入突触中都有可能出现循环状态。它扩展了其他快速权重模型,将STP添加到输入中,并使每个突触的STP可训练。它建立在其他可微可塑性模型的基础上,包括了一个短期方面。它补充了学会学习和学会遗忘。我们将证明,在监督和强化学习(包括元学习的例子)的各种任务中,它是比LSTM更好的RNN选择,超过了最新的快速权重模型,并优于其他可微可塑性机制。STPN的好处包括提高任务熟练度和能源效率。
2. The STPN model
2.1. The model
我们开始构建STPN模型,首先定义一个具有激活hj的简单前馈隐藏单元,该单元接收来自前一层的输入向量x,并通过突触功效向量gj对其进行加权(图1B)。两种实现(图1C)作为直觉,用于在添加STP时将这样的模型作为循环单元。首先,突触后激活hj可能作为可塑性规则的因素之一反馈到输入突触,例如,如果STP是赫布的。其次,每个功效gij的短期记忆和衰退意味着突触包含一个状态变量,该状态变量在时间上部分前向传播。直观地说,这是两个自循环。
我们选择的STPN模型所基于的特定类型的STP是Moratis等人(2020)从理论上提出的。据此,从前一层接收输入向量x的隐藏神经元 j 通过突触功效向量gj对其进行加权,该突触功效向量由两个加性分量组成:gj = wj + fj。STP作用于fj。同时,分量w可以是固定的,或者通过不同的学习规则更新,既可以与STP同时进行,也可以在STP之前进行。在这项工作中,w通过序列之间的外循环中的反向传播进行更新。这个STP规则规定,来自神经元 i 的突触 j 中的fij首先随时间 t 呈指数衰减,其次受与突触前和突触后变量xi和hj成比例的赫布可塑性影响。
基于对两个自递归循环的直觉,我们将STPN构造为一个循环单元,其目的是具有与后一个赫布STP规则类似的功能。我们引入大写符号G = W + F来指示将输入向量连接到隐藏单位向量的矩阵,以及两个大小相等的矩阵![]() 和
和![]() ,包含参数化STP的元素λij和γij。我们将分别用
,包含参数化STP的元素λij和γij。我们将分别用![]() 和
和![]() 来象征元素积和外积。
来象征元素积和外积。
在这个基本版本中,假设固定权重W和非线性函数σ(·),一个时间步骤通过一层STPN单元,由以下方程组描述,其中![]() 表示全一矩阵:
表示全一矩阵:
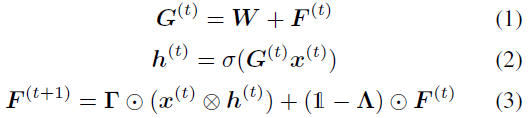
激活h取决于短期分量F到G (公式(1)和(2))。F,反过来,取决于激活及其本身(公式(3)),其中存在该模型的递归性。与标准RNN不同,这种循环不需要隐藏状态hj之间的循环连接,即没有突触连接同一层的单元。在这种情况下,循环是通过参数矩阵![]() 和
和![]() 介导的并将突触状态连接到自身和突触后神经元。因此,该模型实现了一种罕见类型的循环连接,其特征是元权重,即每个突触连接内的连接(图1D中从fij到λij的自循环)(图1D中的蓝色正方形gij)。
介导的并将突触状态连接到自身和突触后神经元。因此,该模型实现了一种罕见类型的循环连接,其特征是元权重,即每个突触连接内的连接(图1D中从fij到λij的自循环)(图1D中的蓝色正方形gij)。
在元学习方面,公式(1)-(3)的赫布STP描述了无监督的内部学习(和遗忘)循环的一次迭代(见第2.3节)。
2.2. Equivalence to STP
可以很简单地表明,STPN结构不仅类似于我们关注的具有赫布STP规则的神经元,而且正是这样——无论是在离散时域中,而不是在连续时域中。规则的原始公式首先规定了随时间的指数衰减,速率为0 < λij < 1:
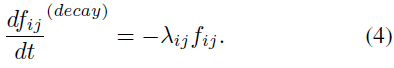
其次,在突触接收输入![]() 的任何离散时间点,具有学习率γij的赫布可塑性也使fij增加一个Δfij,该Δfij也取决于突触后输出
的任何离散时间点,具有学习率γij的赫布可塑性也使fij增加一个Δfij,该Δfij也取决于突触后输出![]() :
:
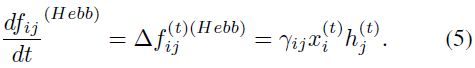
公式(4)和(5)的组合效应描述了完整的原始STP规则。连续时间公式(4)可以通过欧拉方法(Euler, 1794; Kendall et al., 1989)通过小的离散时间步长任意近似:
![]()
长期以来,这种方法一直被用于模拟神经形态模型的持续时间进化,例如脉冲神经元,包括最近((Wozniak et al., 2020)。
另一方面,公式(5)已经只依赖于离散时间事件,因此在离散时间中它仍然是等价的:![]() 。STPN的公式(3)因此可以写成:
。STPN的公式(3)因此可以写成:
![]()
这表明该模型确实相当于离散时间赫布STP。
2.3. Learning to learn and forget with STPN
STPN的参数γij和λij可以用两种方式非常具体地解释。首先,作为循环连接的参数,它们具有明显的短期记忆作用。其次,γ也是突触的赫布学习率,而λ是它的遗忘率。此外,通过将模型构建为基于标准循环加权运算的网络,STPN的参数是可训练的。也就是说,不仅可以训练神经元连接之间的标准W,还可以训练突触内的特征连接。值得注意的是,由于后一种学习连接充当STP的学习和遗忘率,因此训练这些参数可以实现学会学习的方案,也可以学会遗忘。在元学习的这种实现中,内部学习循环是网络通过STP(公式(3))对给定输入序列的在线无监督自适应,而外部学习循环包括网络参数的优化,例如通过时序反向传播(BPTT),用于内部在线学习任务,在该内部任务的多个示例上(参见附录中的算法1)。
2.4. STPN variants
尽管到目前为止,我们已经提供了基于前馈基本结构的STPN描述(公式(2)),但也可以将相同的突触内的连接类型的递归性和可塑性添加到隐藏单元之间具有递归性的模型中,就像简单的RNN一样。这只是简单地改变单元以也接收来自同一隐藏层的输入,即将公式(2)改变为:
![]()
伴随着参数矩阵F和W的大小的相应变化。我们将公式(2)和(8)的网络分别称为STPN连接的STPNf和STPNr变体(用于它们的前馈和全连接,或RNN非可塑性骨架)。该公式可扩展到其他变体,例如添加LSTM门控的STPN的STPNl,尽管这些在本工作中没有进行探索。第4节中的结果是在大多数任务中使用STPNr实现的,除了我们测试STPNf的完全可观察的机器人环境。
3. Methods
3.1. Training methods
我们发现,考虑到我们模型的突触后STP参数的复杂性,特别是对于更复杂的STPN模型,包括突触和神经元之间的循环,如STPNr,训练稳定性和鲁棒性是不可能自动实现的。我们探索了使STPN的训练鲁棒的方法,并得出了一种策略,该策略由我们引入的初始化方法和权重归一化方法组成。详见附录算法1和附录A.4。
3.2. Energy consumption measurement
我们的方法专注于突触加权机制,因此它可以为未来的神经形态硬件提供指导。因此,其能源消耗是一个关键问题。鉴于STP是一种受生物物理学启发的高度神经形态机制,它很可能也是高效的。原则上,STP有可能通过赫布递减和短期衰减灵活而独立地抑制突触电流,这是直观地期望STPN具有高能量效率的原因。考虑到这一点,我们测量了每个模型在假设的模拟神经形态硬件中通过加权操作所产生的功耗。在这样的硬件中,突触前输入x被提供为电压V,而突触效率g的矩阵G可以在具有电导g的电阻器件阵列中表示,例如忆阻器(Sarwat et al., 2022a)。这使得能够通过欧姆定律和基尔霍夫定律进行加权和求和,并导致每个突触的功耗,该功耗与电导g和施加的输入电压的平方V2成比例,如公式(9)所示:
![]()
其中 I 是电流,R是电阻。这种方法使我们能够使用P = x2|g|来测量各种模型的假设功耗。值得注意的是,模拟信号也是通过离子在生物突触中进行突触传递的基础。当生物突触被抑制时,传输的离子更少,电流也更小。因此,在STP是生物学合理的程度上,我们对STPN功耗的测量也为STP在大脑能量预算中的作用提供了一些见解。
3.3. Tested baseline models
在我们的实验中,我们将STPN与其他广泛使用的具有记忆的网络进行了比较,如标准RNN和LSTM,以及其他具有不同类型突触记忆的网络,如具有快速权重的RNN (Ba et al., 2016)和可调节的可塑性RNN (Miconi et al., 2019)。考虑到测试模型之间的定性架构差异,我们通过在每个实验中选择与相同数量的模型参数相对应的隐藏大小,使它们具有可比性。Ba等人(2016)通过向一些连接添加快速权重来增强RNN,特别是在循环神经元之间,即不在前馈突触中,例如从输入层。此外,可塑性的超参数在所有快重突触中都是一致的:赫布更新因子和当前记忆的衰减。此外,他们描述了内环的使用,其中快速权重可以重复作用于中间隐藏状态并被更新,而慢速权重的影响在每次迭代中充当持续的边界条件。然而,他们发现执行多次这样的迭代没有显著的经验益处;在调整这个基线时,我们也不这样做。此外,请注意,这种相同的机制也可以应用于任何其他具有突触记忆的网络,并且在概念上更接近于将相同输入的递归处理作为添加计算资源的一种形式(Schwarzschild et al., 2021a;b; Banino et al., 2021)。快速权重RNN是STPN的一个概念上更简单的版本,主要是因为它只在递归连接上使用可塑性,可塑性规则在神经元和突触中是一致的,而且调节快速学习和遗忘的参数没有经过训练(而是使用验证集进行调整)。由快速权重网络实现的其他机制,如隐藏激活的层归一化,以及通过在输入序列的每个时间步骤上的多次重复迭代来重复应用可塑性。我们的对照实验(未显示)表明,这种迭代方面只提供了很小的改进,并且可以同样应用于STPN。因此,快速权重模型是训练突触特异性STP机制的良好基线。Miconi等人(2018)利用了通过训练参数来优化可塑性的想法,这些参数通过反向传播控制每个突触的记忆,从而产生可微可塑性。Miconi等人(2019)进一步为可塑性增加了一个调节项,类似于三因素可塑性规则中的第三因素,这也是可训练的。与STPN不同,在之前的工作中,没有任何变体可以进化(例如衰减),其效力会随着时间的推移而自发产生,就像STPN一样。我们选择调节可塑性变体(“Modplast”)作为基线,因为它在迷宫探索任务中测试的变体中具有优异的性能(Miconi et al., 2019)。该特定模型中关于STPN的另外两个主要差异是:a)仅在循环突触中具有可塑性,b)每个突触的元训练参数,该参数裁剪了功效的可塑性部分。该模型是可训练可塑性RNN的多种变体中最好的,这是STPN的良好基线。HebbFF (Tyulmankov et al., 2022)在结构上等同于具有均匀可塑性的STPNf。然而,它没有提供每个突触的可塑性参数、神经元之间的循环连接或稳定可塑性更新的机制的选项,如我们在第3节中介绍的机制。这些在复杂度高于(Tyulmankov et al., 2022)中测试的任务中变得必要,我们测试并证实了这一点。具体而言,鉴于HebbFF可以被肤浅地描述为STPN的高度简化版本,我们在附录A.2中包括了与HebbFF以及其他几个更简单的STPN版本的比较。我们还使用具有非突触记忆的网络进行了实验,但这些网络是具有记忆的通用神经网络,并被证明可以通过编码其神经元记忆来执行元学习(Wang et al., 2016)。我们比较了RNN(与STPNr的直接比较,但没有突触STP,与STPNf的记忆类型不同)和LSTM(作为一种更复杂的非可塑性RNN,具有门控和额外的记忆机制)的性能。
3.4. Tested tasks
关联检索任务(ART)(Ba et al., 2016)测试了网络成功存储序列中元素对之间的关联的能力,并在与序列末尾的另一个(密钥)一起查询时检索该对中的一个元素(值)。因此,这项任务和其他变体(Schlag & Schmidhuber, 2017; Le et al., 2020)通常用于比较具有不同性质记忆的网络的能力。对于这项任务的设置,除了附录A.5.1中描述的修改外,我们主要遵循Ba等人(2016)中提供的实验细节。迷宫探索:迷宫式或类似网格的任务通常用于RL中,作为一种数据高效且可解释的任务来测试RL算法。(Miconi et al., 2018)实例化了这种迷宫的一种特定形式,在这种迷宫中,智能体对周围环境有一种以自我为中心的看法,其目标是导航到一个奖励,但它看不到,其位置在不同的回合中是随机的。此外,在发现奖励时以及在一个回合开始时,智能体被随机重新定位到网格中的另一个位置。考虑到这种环境设计,我们可以将迷宫探索任务视为对智能体元学习能力的测试。首先,每个迷宫实例化(具有固定的奖励位置)代表了学习的内环,因为智能体需要学习如何有效地导航到这个新的奖励位置,并在发现奖励时从重新定位后的每个初始随机位置开始这样做。其次,在不同的回合中,需要优化参数,以便在内环内和通过迷宫的不同实例化提供帮助,从而学会学习。此外,即使在一个回合中,我们也可以区分两个定性不同的阶段:在第一步中,智能体需要探索迷宫的实例化,以找到奖励位置。一旦了解到目标的定位,它就会进入一个开发阶段,在这个阶段,关键是快速达到已经看到的奖励。这两个任务分布(所有可能迷宫的分布和二值探索-开发阶段)将该任务定位为具有记忆的非可塑性和可塑性网络的元学习和序列自适应能力的良好基准。Atari游戏和MuJoco模拟机器人:前两个实验装置,即ART和迷宫探索,在可塑性相关文章中介绍,具有一些可能有利于可塑连接模型的特征。RL是一个研究领域,在该领域,RNN及其变体在SOTA算法中的使用仍然广泛,与语言、视频或音频的监督学习领域相比更是如此。为了超越可塑性网络文献所局限的简单任务,为了探索RNN是SOTA方法组成部分的领域,并为了研究STPN作为具有存储器的通用网络的使用,我们用两个常见的深度RL基准的两个任务进行了一些初步实验:Atari Pong和MuJoCo Inverted Pendulum。Pong是一款在街机学习环境(ALE)(Bellemare et al., 2013)中实现的Atari 2600游戏,玩家面对对手,每个玩家都控制一个杆,他们可以上下移动以击球,从而进球或阻止对手这样做。当玩家达到21分时,游戏停止。智能体获得的奖励是完成游戏的净得分,观察结果是游戏框架。对于我们在Pong中的实验,我们使用A2C,即A3C的同步版本(Mnih et al., 2016)作为学习算法。智能体的网络使用卷积层,如Mnih等人(2016)中的卷积层、递归策略(由价值和行动分支共享)以及非可塑性前馈价值和动作支路。像A2C这样的简单算法可以更好地探索递归单元的真实影响,它之前在迷宫任务中的使用为我们提供了一些与可塑性网络兼容的保证。除了从toy、可塑性网络的任务转移领域之外,Pong还提供了第一种情况,即STPN嵌入到更大的网络中,其输入不是稀疏的,直接来自环境,而是密集的,是多层处理的结果。请注意,由于我们不执行帧堆叠,因此环境是部分可观察的马尔可夫决策过程(POMDP),因为球的速度不能从单个帧中推断出来(Hausknecht & Stone, 2015)。对具有内存的智能体的这种需求证明了使用递归策略以及缺乏与前馈策略的比较是合理的。MuJoCo (Todorov et al., 2012)是一种广泛用于机器人和强化学习研究的物理引擎。Inverted Pendulum是MuJoCo中最简单的任务之一,智能体的目标是通过连续值控制在一维上前后移动推车,来平衡推车上的倒立摆。我们对MuJoCo倒立摆的实验代表着在机器人和连续控制中更复杂的问题(如MuJoCo环境中的问题)中使用STPN,并结合更先进的RL算法(如本例中的近端策略优化(PPO)算法)(Schulman et al., 2017),朝着使用STPN的方向迈出了初步的一步。与没有帧堆叠的Pong不同,Inverted Pendulum是一个完全可观测的马尔可夫决策过程(MDP),因此不需要对过去的记忆来评估现在或预测未来。因此,训练处理隐藏记忆的参数可能意味着在信度分配方面付出了不必要的努力,而隐藏状态的维度比环境观测的维度大得多,这会加剧这种情况。因此,我们在这种情况下使用STPNf,并将MLP作为基线;除了RNN和LSTM之外。关于我们用于不同时间尺度(如回合、epoch、时间步骤)的术语,请参见附录A.6。
4. Results
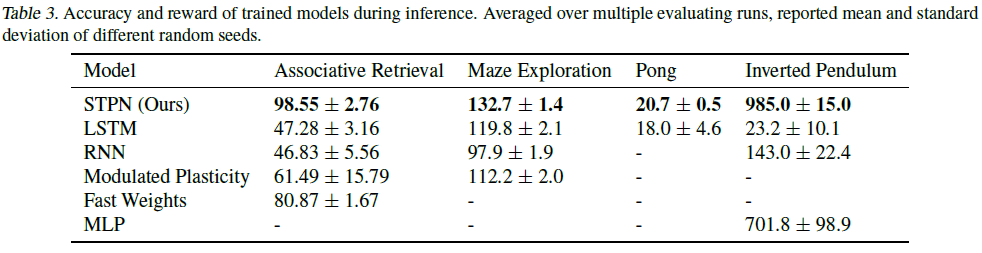
4.1. Accuracy & reward
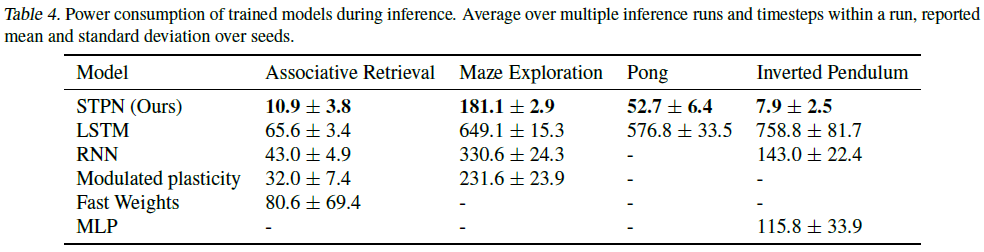
4.2. Energy consumption
4.3. Learning to learn and forget
5. Discussion
STPN建立在先前的理论最优性证明和生物学证据的基础上。因此,通过将可单独训练的短期可塑性引入所有突触,STPN比各种其他模型更具表现力、效率更高,能够更好地学习和忘记,并且在各种困难任务中都能做到这一点。该模型还提供了一种提高神经形态平台效率的新方法。结合先前支持我们可塑性的生物学合理性的实验证据,我们的研究结果也提高了STP对动物行为和大脑能量预算的重要性。这一成果为RNN、元学习、神经形态计算和神经科学领域的跨学科研究开辟了新的途径,我们希望这些领域能够得到探索。
A. Appendix
A.1. The meta-learning algorithm

A.2. Importance of learning per-synapse STP parameters
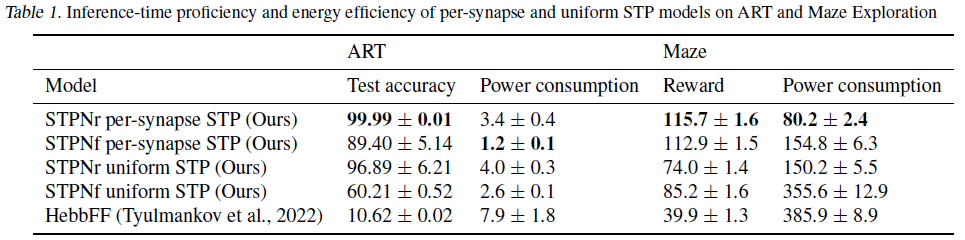
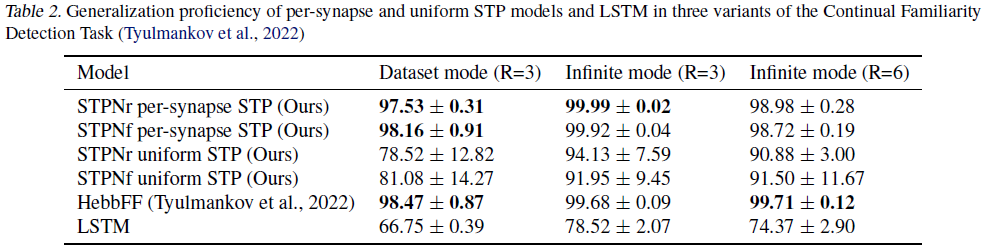
A.3. Further results
A.4. Training methods
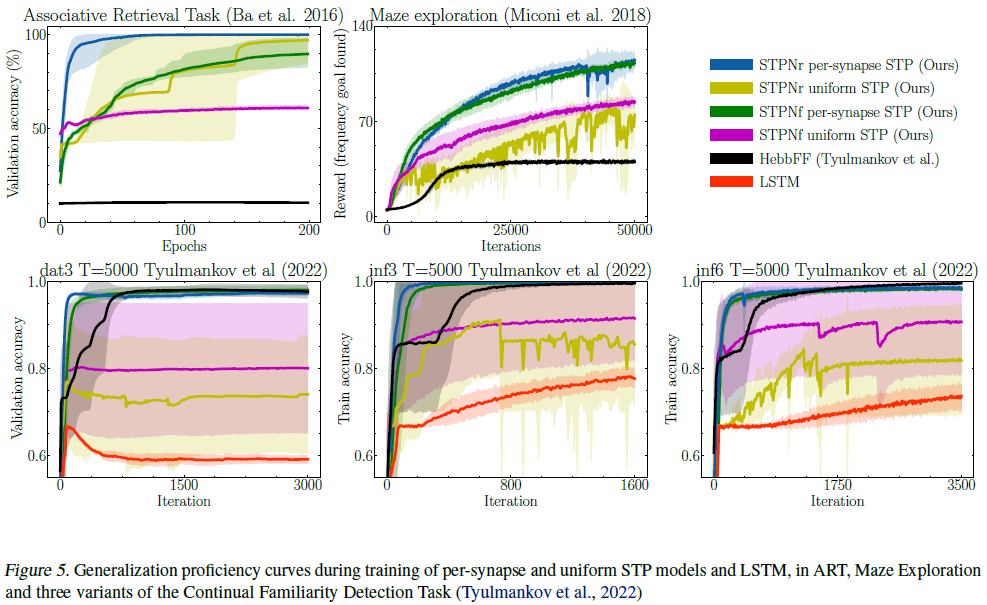
A.5. Experimental details
我们在实验中运行了不同数量的种子,当其中一个或两个实验的计算成本不高,或者需要更多的实例来得出更清晰的结论时,我们会运行更多的种子。具体来说,我们分别使用了5个(ART和Pong)、3个(Maze)和2个(Pendulum)种子。
A.5.1. ASSOCIATIVE RETRIEVAL
A.5.2. MAZE EXPLORATION
A.5.3. ATARI PONG
我们使用RLLib (Liang et al., 2018)来训练和评估PongNoFrameskip-v4中的智能体。除了第3.4节中描述的实验选择外,应该注意的是,我们使用具有64个隐藏单元的STPNr,并将LSTM的大小调整为48个隐藏单元,以便具有类似数量的可训练参数。我们还遵循了Mnih等人(2016)对游戏帧的预处理(维度和色阶),除了帧堆叠。我们在较短的运行中调整rollout长度(50)、梯度剪裁(40)、折扣系数(0.99)(这两个模型在显示的结果中共享);并使用在2亿次迭代中以10-11结束的线性衰减学习率计划,额外调整最后较长运行的初始学习率(分别为0.0007和0.0001)。模型是根据64个并行智能体收集的经验进行训练的。
A.5.4. MUJOCO INVERTED PENDULUM
我们使用RLLib来训练和评估InvertedPendulum-v2中的智能体。我们主要使用(Schulman et al., 2017)中报告的相同参数进行操作,对于其中未指定的任何其他参数,我们使用RLLib提供的默认选项。唯一的区别是:a)使用线性衰减的学习率时间表,从相同的原始学习率开始,以400万个时间步骤结束在10-11;b)由于(Schulman et al., 2017)中没有具体说明,我们使用一个并行工作者在一个环境中收集经验;c)选择大小为64的单层策略网络(除去动作和价值分支外)(这是唯一一种没有调整模型隐藏大小以获得类似数量参数的情况,因为它在我们的实验中没有被证明是相关的)。
A.6. Terminology on timescales
A.7. STPN mechanics





 浙公网安备 33010602011771号
浙公网安备 33010602011771号