Robust Deep Reinforcement Learning against Adversarial Perturbations on State Observations

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, Canada.

 

Abstract

　　深度强化学习（DRL）智能体通过观察来观察其状态，其中可能包含自然测量误差或对抗性噪声。由于观察结果偏离了真实状态，它们可能会误导智能体做出次优行为。一些工作已经通过对抗性攻击显示了这种脆弱性，但在这种情况下提高DRL鲁棒性的现有方法成功率有限，缺乏理论原则。我们表明，天真地应用现有技术来提高分类任务的鲁棒性，如对抗性训练，对于许多RL任务是无效的。我们提出了状态对抗性马尔可夫决策过程（SA-MDP）来研究这个问题的基本性质，并开发了一种理论上有原则的策略正则化，它可以应用于一大类DRL算法，包括近端策略优化（PPO）、深度确定性策略梯度（DDPG）和深度Q网络（DQN），用于离散和连续动作控制问题。我们在一系列强白盒对抗性攻击（包括我们自己的新攻击）下显著提高了PPO、DDPG和DQN智能体的鲁棒性。此外，我们发现，即使在许多环境中没有对手，鲁棒的策略也能显著提高DRL性能。我们的代码可在https://github.com/chenhongge/StateAdvDRL中获取。

 

1 Introduction

　　凭借深度神经网络（DNN）作为强大的函数逼近器，深度强化学习（DRL）在许多复杂任务[46，35，33，64，20]甚至在一些安全关键应用（如自动驾驶[74，56，49]）上都取得了巨大成功。尽管在许多任务上实现了超人类级别的性能，但DNN中存在的对抗性示例[69]以及对DRL的许多成功攻击[27，4，36，50，81]激励我们研究鲁棒的DRL算法。

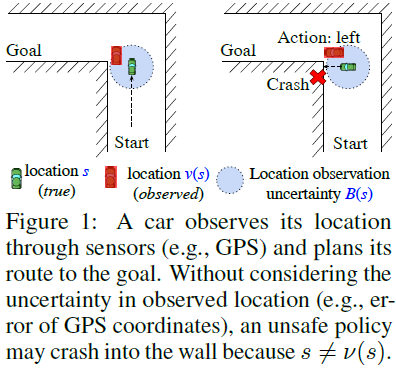
　　当RL智能体通过观测获得其当前状态时，观测可能包含不确定性，这种不确定性自然源于不可避免的传感器错误或设备不准确。对这种不确定性不鲁棒的策略可能会导致灾难性故障（例如，图1中的导航设置）。为了确保在最坏情况下的不确定性下的安全性，我们考虑对抗性设置，其中状态观测从s到ν(s)受到对抗性扰动，但潜在的真实环境状态s不变。这种设置与许多对状态观测的对抗性攻击一致（例如，[27，36]），并且不能用现有的工具（如部分可观测马尔可夫决策过程（POMDP））来表征，因为POMDP中的条件观测概率不能捕捉对抗性（最坏情况）场景。在这种情况下研究基本原则至关重要。

　　在制定基本原则之前，一些早期的方法[5，40，50]扩展了现有的对抗性防御，用于监督学习，例如对抗性训练[32，39，87]，以提高这种情况下的鲁棒性。具体来说，我们可以在训练时间内攻击智能体并生成对抗性轨迹，并应用任何现有的DRL算法来有望获得鲁棒的策略。不幸的是，我们发现，对于大多数环境，幼稚的对抗性训练（例如，将对抗性状态放入回放缓存）会导致不稳定的训练并恶化智能体性能[5，15]，或者在强攻击下不能显著提高鲁棒性。由于RL和监督学习是完全不同的问题，在没有适当理论依据的情况下天真地将监督学习的技术应用于RL可能是不成功的。总之，我们研究了鲁棒RL对状态观测扰动的理论和实践：

• 我们将状态观测的扰动公式化为一个修正的马尔可夫决策过程（MDP），我们称之为状态对抗性MDP（SA-MDP）并研究其基本性质。我们证明了在最优对手下，SA-MDP可能不存在平稳的马尔可夫最优策略。
• 基于我们的SA-MDP理论，我们提出了一个理论上有原则的鲁棒策略正则器，该正则器与扰动策略的总方差距离或KL散度有关。它可以实际有效地应用于各种RL算法，包括PPO、DDPG和DQN。
• 我们在10个环境中进行了实验，从具有离散动作的Atari游戏到连续动作空间中的复杂控制任务。我们提出的方法显著提高了在对状态观测的强白盒攻击下的鲁棒性，包括我们设计的两种强攻击，鲁棒Sarsa攻击（RS攻击）和最大动作差攻击（MAD攻击）。

 

2 Related Work

Robust Reinforcement Learning 由于RL的每个元素（观察、动作、转移动力学和奖励）都可能包含不确定性，因此从不同的角度对鲁棒RL进行了研究。鲁棒马尔可夫决策过程（RMDP）[29，47]考虑了来自转移概率的最坏情况扰动，并已扩展到分布设置[82]和部分观察到的MDP[48]。智能体从环境中观察原始真实状态并相应地采取动作，但环境可以从一组最小化奖励的转移概率中进行选择。与对手只改变观测值的SA-MDP相比，在RMDP中，真实状态发生了变化，因此RMDP更适合对环境参数变化（例如，质量和长度等物理参数的变化）进行建模。RMDP理论启发了鲁棒的深度Q学习[62]和策略梯度算法[41，12，42]，它们对小的环境变化是鲁棒的。

　　另一系列工作[51，34]考虑了多智能体强化学习的对抗性设置[70，9]。在最简单的双人游戏设置（称为最小最大游戏[37]）中，每个智能体在每一步都选择一个动作，环境基于这两个动作进行转换。正则Q函数Q(s, a)可以扩展到Q(S, a, o)，其中o是对手的动作，Q学习仍然收敛。此设置可以扩展到深度Q学习和策略梯度算法[34，51]。Pinto等人[51]表明，同时学习对手可以提高智能体的性能，以及其对环境湍流和测试条件（例如质量或摩擦的变化）的鲁棒性。Gu等人[21]对两人对抗性学习游戏进行了真实世界的实验。Tessler等人[71]考虑了动作空间上的对抗性扰动。Fu等人[16]研究了如何学习强大的奖励。所有这些设置都与我们的不同：我们只操纵状态观测，但不会直接改变底层环境（真实状态）。

Adversarial Attacks on State Observations in DRL Huang等人[27]通过对具有离散动作的Atari游戏进行基于FGSM的攻击，评估了深度强化学习策略的鲁棒性。Kos和Song[31]提出使用价值函数来指导对抗性扰动搜索。Lin等人[36]考虑了一种更复杂的情况，即对手只被允许攻击一个子集的时间步长，并使用生成模型来生成攻击计划，将智能体引诱到指定的目标状态。Behzadan和Munir[4]通过对抗性示例的可转移性研究了离散动作对DQN的黑盒攻击。Pattanaik等人[50]通过多步梯度下降和更好的损失函数，进一步增强了对DRL的对抗性攻击。它们需要一个评判器或Q函数来执行攻击。通常，使用在智能体训练过程中学到的评判器。我们发现，在许多情况下，使用这个评判器可能是次优的或不切实际的，并在第3.5节中提出了我们的两个独立于评判器的强攻击（RS和MAD攻击）。我们请读者参考最近的调查[81，28]，了解DRL环境中对抗性攻击的分类法和全面列表。

Improving Robustness for State Observations in DRL 对于离散动作RL任务，Kos和Song[31]首先提出了在Pong（最简单的Atari环境之一）上使用像素空间上的弱FGSM攻击进行对抗性训练的初步结果。Behzadan和Munir[5]将对抗性训练应用于几场带有DQN的Atari游戏，发现智能体在训练期间很难适应攻击。这些早期的方法取得了比我们差得多的结果：对于Pong来说，Behzadan和Munir[5]可以在来自-21（最低）至-5，但距离最佳奖励（+21）仍然很远。最近，Mirman等人[43]，Fischer等人[15]将DQN的离散动作输出视为标签，并应用现有的认证防御进行分类[44]，以使用模仿学习来鲁棒地预测动作。这种方法优于[5]，但尚不清楚如何将其应用于具有连续动作空间的环境。与他们的方法相比，我们的SA-DQN不使用模仿学习，在大多数环境中都能获得更好的性能。

　　对于连续动作RL任务（例如，OpenAI Gym中的MuJoCo环境），Mandlekar等人。[40]使用具有策略梯度的基于弱FGSM的攻击来对抗性地训练一些简单的RL任务。Pattanaik等人[50]使用了更强的基于梯度的多步骤攻击；然而，他们的评估重点是对环境变化的鲁棒性，而不是状态扰动。与我们的工作不同，我们的工作首先开发原理，然后应用于不同的DRL算法，这些工作直接将监督学习中的对抗性训练扩展到DRL设置，并且在第4节中没有可靠地提高强攻击下的测试时间性能。一项并行工作[63]考虑了与我们类似的平滑正则器，但他们使用虚拟对抗性训练，并专注于提高泛化能力，而不是鲁棒性。我们为我们的正则器提供了理论依据，提出了新的攻击，并在强大的对手下进行了全面的实证评估。

　　其他相关工作包括[24]，它提出了一种元在线学习过程，其中主智能体检测对手的存在并在几个子策略之间切换，但没有讨论如何鲁棒地训练单个智能体。[11]专门针对基于RL的路径查找算法应用对抗性训练。[38]考虑了现有DQN智能体在rollout期间的最坏情况，以确保安全，但它依赖于现有策略，不包括训练程序。

 

3 Methodology

3.1 State-Adversarial Markov Decision Process (SA-MDP)

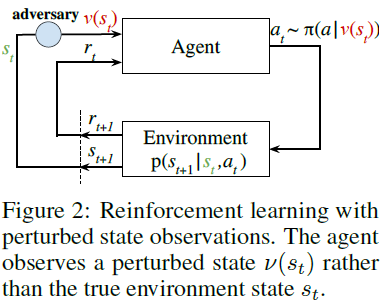
　　在状态对抗性MDP（SA-MDP）中，我们引入了一个对手ν(s)：S→S¹。对手只干扰智能体的状态观测，使得动作被视为π(a|v(s))；环境仍然从真实状态s而不是v(s)转移到下一状态。由于v(s)可以不同于s，因此来自π(a|v(s))的智能体的动作可能是次优的，因此对手能够减少奖励。在现实世界的RL问题中，对手可以反映为测量或状态估计不确定性中的最坏情况噪声。请注意，这种场景不同于两人马尔可夫博弈[37]，其中两人都看到未受干扰的真实环境状态，并直接与环境交互；对手的动作可以改变比赛的真实状态。

　　为了进行正式分析，我们首先对对手v进行假设：

　　这一假设适用于许多对抗性攻击[27，36，31，50]。这些攻击只依赖于当前状态输入和策略或Q网络，因此它们是马尔可夫的；网络参数在测试时被冻结，因此给定相同的s，对手将产生相同的（静止的）扰动。我们把对非马尔可夫且非平稳对手的正式分析留给未来的工作。

　　如果对手可以无边界地任意扰动状态s，则问题可能变得微不足道。为了使我们的分析符合最现实的情况，我们需要限制对手的力量。我们定义了扰动集B(s)，以限制对手仅将状态s扰动到预定义的状态集：

　　B(s)通常是s的一组特定于任务的“相邻”状态（例如，有界传感器测量误差），这使得即使有扰动，观测仍然有意义（但不准确）。定义B后，SA-MDP可以表示为6元组（S, A, B, R, p, γ）。

Analysis of SA-MDP 我们首先推导了Bellman方程和一个基本的策略评估过程，然后讨论了获得SA-MDP最优策略的可能性。在v下，SA-MDP中的对抗性价值和动作-价值函数类似于常规MDP：

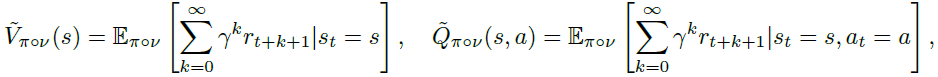
其中步骤 t 处的奖励被定义为r_t，并且表示在观测扰动下的策略：π(a|v(s))。基于这两个定义，我们首先考虑具有固定π和v的最简单情况：

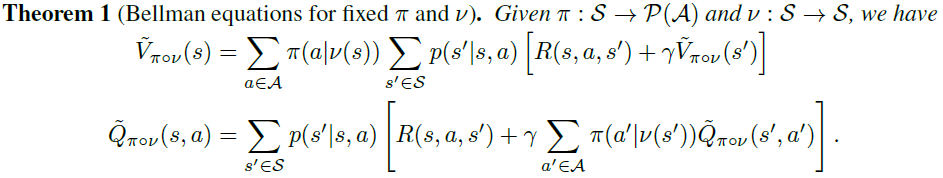
　　定理1的证明很简单，比如当π, v是固定的，可以将它们“合并”为单个策略，并且可以直接应用MDP的现有结果。现在我们考虑一个更复杂的情况，我们想找到最优对手v*(π)下的价值函数，使固定目标的总期望奖励最小化。最优对抗性价值和动作-价值函数被定义为：

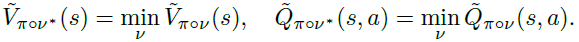
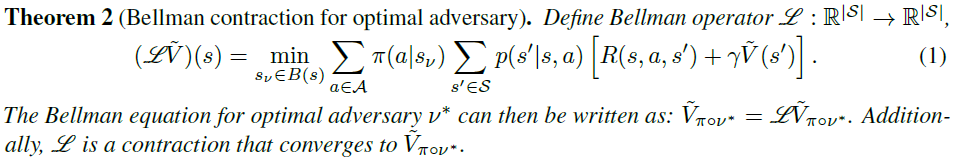
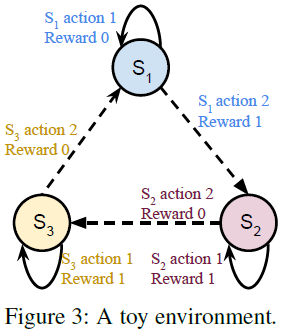
　　定理2表明，给定一个固定的策略，我们可以通过Bellman收缩来评估其在最优（最强）对手下的性能（价值函数）。它在功能上类似于常规MDP中的“策略评估”程序。定理2的证明与求解MDP最优策略的Bellman最优方程的证明具有相同的精神；这里的重要区别在于，对于固定策略π，我们求解最优对手。给定的情况下，MDP和SA-MDP的价值函数可能有很大的不同。在图3中，我们展示了一个三状态toy环境；最优MDP策略是在S₁中采取动作2、在S2和S3中采取动作1。在存在对手v(S₁)＝S₂, v(S₂)＝S₁, v(S₃)＝S₁的情况下，该策略获得零总奖励，因为无论状态如何，对手都可能使动作π(a|v(s))完全错误。另一方面，对所有三种状态采取随机动作的策略（这是MDP的非最优策略）不受对手的影响，并在SA-MDP中获得非零奖励。详细信息见附录A。

　　最后，我们讨论了在SA-MDP设置中，在最强对手v*(π)下找到最优策略π*的最终追求（我们使用符号v*(π)来明确表示v*是给定π的最优对手）。最优策略应该是每个状态所有策略中最好的：

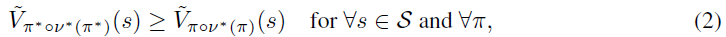
其中π和v都不是固定的。第一个问题是，我们需要为π*考虑哪些策略类别。在MDP中，确定性策略就足够了。我们表明，这在SA-MDP中不再适用：

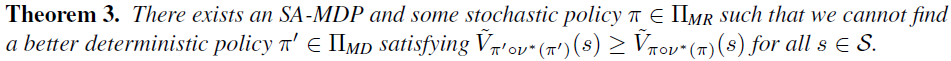
　　证明是通过构建一个反例来完成的，其中一些随机策略比SA-MDP中的任何其他确定性策略都要好（见附录A）。相反，在MDP中，对于任何随机策略，我们都可以找到一个至少与随机策略一样好的确定性策略。不幸的是，即使同时寻找确定性和随机性策略，也无法始终找到最优策略：

　　该证明遵循与定理3中相同的反例。最优策略π*要求对所有s和任意一个π都有。在SA-MDP中，有时我们必须在状态的值之间进行权衡，并且没有任何策略可以最大化所有状态的价值。

　　尽管在最优对手下很难找到最优策略，但我们表明，在某些假设下，最优对手造成的性能损失是有界的：

　　定理5表明，只要状态扰动下的动作分布之间的差异（项）不太大，则（SA-MDP的状态价值）和V_π(s)（常规MDP的状态价值）之间的性能差距可以是有界的。一个重要的后果是正则化的动机，以获得对强大对手强有力的策略。该证明基于在约束策略优化[1]中开发的工具，该工具给出了给定两个具有有界分歧的策略的价值函数的上界。在我们的情况下，我们希望有界状态扰动在和之间产生有界发散。

　　我们现在研究了一些实用的DRL算法，包括用于离散动作的深度Q学习（DQN）和用于连续动作的基于行动器-评判器的策略梯度方法（DDPG和PPO）。

 

¹ 我们的分析也适用于随机对手。最佳对手是确定性的（见引理1）。

 

3.2 State-Adversarial DRL for Stochastic Policies: A Case Study on PPO

 

3.3 State-Adversarial DRL for Deterministic Policies: A Case Study on DDPG

 

3.4 State-Adversarial DRL for Q Learning: A Case Study on DQN

　　DQN的动作空间是有限的，并且确定性动作由最大Q值确定：当时，π(a|s)＝1，否则为0。这种情况下的总方差距离为：

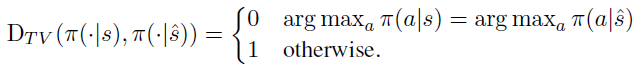
　　因此，我们希望使top-1动作在扰动后保持不变，并且我们可以使用类似铰链的鲁棒策略正则器，其中且c是一个小的正常数：

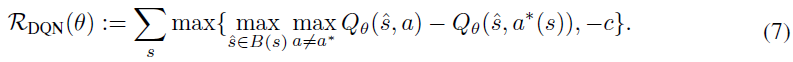
　　总和是一个采样批次中所有s的总和。其他损失函数（例如，交叉熵）也是可能的，只要目的是保持top-1动作在扰动后保持不变。这种设置类似于分类任务的鲁棒性，如果我们将a*(s)视为“正确”标签，因此可以应用许多鲁棒分类技术，如[43，15]所示。最大化可以使用投影梯度下降（PGD）或神经网络的凸松弛来解决。由于它与分类相似，我们将解决R_DQN(θ)和完整SA-DQN算法的细节推迟到附录H中。

 

3.5 Robust Sarsa (RS) and Maximal Action Difference (MAD) Attacks

 

4 Experiments

　　在我们的实验²中，对抗性状态集合B(s)被定义为围绕s的“l_∞范数球”，半径为ε：。这里也被称为扰动预算。在MuJoCo环境中，l_∞范数应用于归一化状态表征。

Evaluation of SA-PPO

Evaluation of SA-DDPG

Evaluation of SA-DQN 我们在四款Atari游戏上实现了Double DQN[72]（PS：官方源码未实现Double DQN，而是Dueling DQN）和Prioritized Experience Replay[58]。我们为朴素DQN和SA-DQN训练Atari智能体600万帧。详细的参数和训练过程见附录H。我们将像素值归一化为[0, 1]，并添加范数ε=1/255的l_∞对抗性噪声。我们包括普通DQN和对抗性训练的DQN，其中50%的帧在训练时间内受到攻击[5]作为基线，我们报告了鲁棒模仿学习的结果[15]。我们评估了10步非目标PGD攻击下的所有环境，除了[15]的结果是使用较弱的4步PGD攻击进行评估的。对于最鲁棒的Atari智能体（SA-DQN convex），我们使用50步PGD攻击对其进行额外攻击，并发现奖励不会进一步减少。在表3中，我们看到，在大多数环境中，我们的SA-DQN在攻击下获得了更高的奖励，而在强攻击下，幼稚的对抗性训练大多无效。在大多数环境中，我们获得了比[15]更好的奖励，因为我们直接学习智能体，而不是使用两步模仿学习。

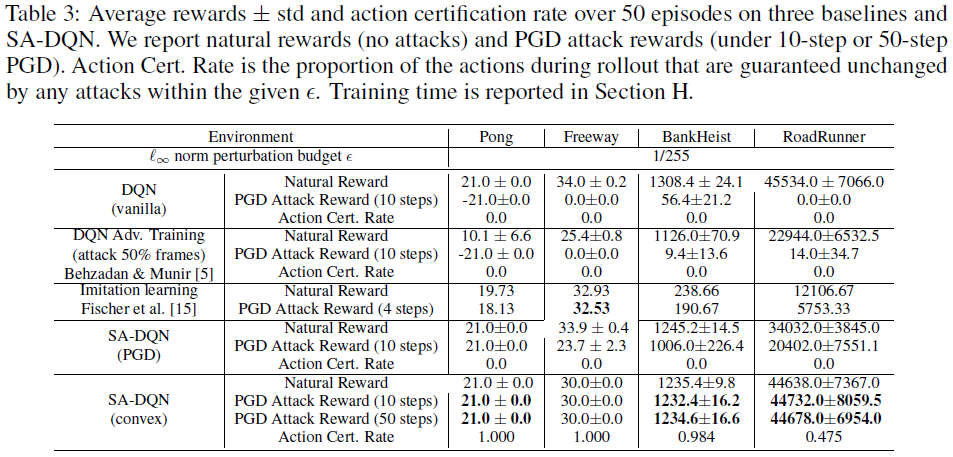
Robustness certificates. 当我们的鲁棒策略正则器使用凸松弛进行训练时，我们可以在观测扰动下获得一定的鲁棒性认证。对于Pong这样的简单环境，我们可以保证在rollout过程中所有帧的动作都不会改变，从而保证在扰动下的累积奖励。对于SA-DDPG，在所有5种环境中，动作变化的最大l₂差异的上限比基线小几倍（见附录I）。不幸的是，对于大多数RL任务，由于环境动力学和奖励过程的复杂性，不可能获得“认证奖励”作为监督学习设置中的认证测试错误[79，88]。我们在附录E中留下了关于这些挑战的进一步讨论。

 

² 代码和预训练智能体可在https://github.com/chenhongge/StateAdvDRL中获取

 

Broader Impact

　　强化学习是现代人工智能的核心部分，近年来仍在大力发展。与在许多商业和工业应用中广泛部署的监督学习不同，强化学习尚未在现实世界中被广泛接受和部署。因此，对抗性攻击环境下的强化学习鲁棒性研究受到的关注少于监督学习。

　　然而，随着最近强化学习在许多复杂游戏上的成功，如Go[65]、StartCraft[73]和Dota 2[6]，如果我们在不久的将来看到强化学习（尤其是深度强化学习）被用于日常决策任务，我们不会感到惊讶。因此，在广泛部署强化学习智能体之前，必须对其应用的潜在社会影响进行调查。一个重要的方面是智能体的可信度，其中鲁棒性起着至关重要的作用。本文中考虑的鲁棒性对于DRL系统的许多实际设置（如传感器噪声、测量误差和中间人（MITM）攻击）很重要。如果能够建立强化学习的鲁棒性，它就有很大的潜力应用于许多关键任务，如自动驾驶[60，56，85]，以实现超人的性能。

　　另一方面，将强化学习应用于现实情况（围棋和星际争霸等游戏之外）的一个障碍是“现实差距”：模拟环境中训练有素的强化学习智能体很容易在现实世界的实验中失败。这种失败的一个原因是现实世界环境中潜在的传感错误；早在1992年的Brooks[8]中就讨论过这一点，现在仍然是一个悬而未决的挑战。尽管我们的实验是在模拟环境中进行的，但我们相信，像我们论文中提出的平滑正则器也可以使在现实世界环境中测试的智能体受益，例如机器人手操纵[2]。

 

Appendix

 

A　An example of SA-MDP

 

B　Proofs for State-Adversarial Markov Decision Process

 

C　Optimization Techniques

C.1　More Backgrounds for Convex Relaxation of Neural Networks

　　在我们的工作中，我们经常需要解决一个极小极大问题：

　　我们将讨论的一种方法是首先使用类似SGLD的优化器（近似地）解决内部最大化问题。然而，由于的非凸性，我们无法将内部最大化解为全局最大值，并且局部最大值和全局最大值之间的差距可能很大。使用神经网络的凸松弛，我们可以找到的上界：

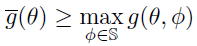
　　因此，我们可以最小化上限，这可以保证原始目标(27)最小化。

（待续）

 

C.2　Solving the Robust Policy Regularizer using SGLD

 

D　Additional details for adversarial attacks on state observations

D.1　More details on the Critic based attack

　　在第3.5节中，我们讨论了基于评判器的攻击[50]作为基线。这种攻击需要Q函数Q(s, a)来找到最优扰动状态。在算法2中，我们提出了基于[50]的“修正”的基于评判器的攻击：

 

D.2　More details on the Maximal Action Difference (MAD) attack

 

D.3　More details on the Robust Sarsa attack

 

D.4　Hybrid RS+MAD attack

 

D.5　Projected Gradient Decent (PGD) Attack for DQN

　　对于DQN，我们使用文献[36，50，81]中的常规无目标投影梯度衰减（PGD）攻击。具有K次迭代的无目标PGD攻击将状态更新K次，如下所示：

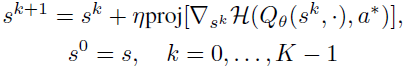
其中H(Q_θ(s^k, ·), a*)是Q_θ(s^k, ·)的输出logits和的onehot编码分布之间的交叉熵损失。proj[·]是取决于B(s)的范数约束的投影算子，并且η是学习率。成功的无目标PGD攻击将扰乱状态，导致Q网络输出除在原始状态s选择的最优动作a*之外的动作。为了保证攻击获得的最终状态在s周围的l_∞球内（），投影proj[·]是一个符号运算符，η通常设置为。

 

E　Robustness Certificates for Deep Reinforcement Learning

　　如果我们使用第C.1节中的凸松弛来训练我们的网络，它可以为我们的任务生成鲁棒性证书[79，44，88]。然而，在一些RL任务中，证书具有不同于分类任务的解释，如下面详细讨论的。

Robustness Certificates for DQN. 在DQN中，动作空间是有限的，因此我们有一个关于在每个状态下采取的动作的鲁棒性证书。更具体地说，在每个状态s，如果其相应的Q函数满足下式，则策略的动作是认证的：

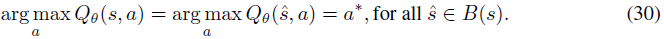
给定状态s，我们可以使用神经网络凸松弛来计算上限使得：

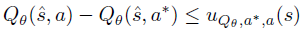
适用于所有。所以如果对所有都有，我们可得：

对于所有都是有保证的，这意味着当状态观测处于B(s)时，智能体的动作不会改变。当智能体的动作在对抗性扰动下没有改变时，其在当前步骤的奖励和转换在DQN设置中也不会改变。

　　在某些设置中，我们发现100%的动作保证不变（例如，表3中的Pong环境）。在这种情况下，我们实际上也可以证明，在测试的特定初始条件下，累积奖励没有改变。否则，如果roll-out过程中的某些步骤没有此证书，或者有一个较弱的证书，即在给定的情况下可以执行多个动作，则必须将所有可能的动作作为环境的下一个动作输入。当有n个状态没有被证明具有不变的动作，每个状态都有m个可能的动作时，我们需要运行n^m个轨迹来找到最坏情况下的累积奖励。这对于典型的设置是不切实际的。

　　然而，即使在Pong这样的100%证书率设置中，证明智能体在任何启动条件下都是鲁棒的仍然是一项挑战。由于智能体是从随机初始化开始的，因此枚举所有可能的初始化并保证所有生成的轨迹都经过验证是不切实际的。类似地，在分类设置中，许多现有的认证防御[80，44，19，88]实际上只能保证特定测试集的鲁棒性（通过计算“验证的测试误差”），而不能保证任何输入图像的鲁棒性。

Robustness Certificates for PPO and DDPG.

 

F　Additional details for SA-PPO

 

G　Additional Details for SA-DDPG

 

H　Additional Details for SA-DQN

Algorithm 我们在算法7中提出了SA-DQN训练算法。SA-DQN和DQN之间的主要区别是额外的状态对抗正则器R_DQN(θ)，它鼓励网络在状态观测的扰动下不改变其输出。我们在算法7中强调了这些变化。请注意，不需要使用铰链损失；也可以使用其他损失函数（例如交叉熵损失）。

Hyperparameters for Vanilla DQN training. 对于Atari游戏，深度Q网络有3个CNN层，然后是2个全连接层（如下[77]）。第一个CNN层有32个通道，核大小为8，步长为4。第二个CNN层有64个通道，核大小为4，步长为2。第三个CNN层有64个通道，核大小为3，步长为1。全连接层具有512个隐藏神经元，用于价值和优势头部。我们在没有帧堆叠的情况下运行每个环境6×10⁶个步骤。我们将学习率设置为6.25×10^-5（遵从[26]），适用于Pong、Freeway和RoadRunner；对于BankHeist，我们的实现无法在600万步内可靠地收敛，因此我们将学习率降低到1×10^-5。对于所有Atari环境，我们将奖励剪辑到-1, +1（遵从[46]），并使用容量为2×10⁵的回放缓存。

　　我们将折扣系数设置为0.99。优先回放缓存采样使用α=0.5，并且β在训练时从0.4线性增加到1。在训练中使用32的批大小。与[46]中相同，我们选择Huber损失作为TD损失。我们为所有环境每2k步更新一次目标网络。

Hyperparameters for SA-DQN training. SA-DQN使用与DQN训练中相同的网络结构和超参数。所有环境中SA-DQN训练步骤的总数与DQN中的相同（600万）。对于所有环境，我们每2k步更新一次目标网络，除了RoadRunner的SA-DQN每32k步更新一个目标网络之外，这提高了我们600万帧的短训练计划的收敛性。对于用于鲁棒性的附加状态对抗性正则化参数κ，我们选择κ∈{0.005, 0.01, 0.02}。对于所有4个Atari环境，我们在没有正则化的情况下训练Q网络的前1.5×10⁶步，然后在4×10⁶步中将ε从0增加到目标值，然后在剩下的5×10⁵步中保持在目标ε上训练。

Training Time 由于Atari训练成本高昂，我们只训练了600万帧DQN和SA-DQN；大多数DQN论文（例如[46，77，26]）中报告的奖励是通过训练2000万帧来获得的。因此，报告的奖励（没有攻击）可能低于一些基线。在单个1080 Ti GPU上，朴素DQN、SA-DQN（SGLD）和SA-DQN（convex）的训练时间分别约为15小时、40小时和50小时。每个环境的训练时间各不相同，但非常接近。

　　注意，当使用更有效的松弛时，可以进一步减少基于凸松弛的方法的训练时间。最快的松弛是区间约束传播（IBP），但它太不准确，会使训练不稳定且难以调整[88]。我们使用更严格的IBP+Backward松弛，通过最近开发的损失融合技术[83]，其复杂性可以进一步提高到与IBP相同的水平，同时提供比IBP更好的松弛。我们的工作只是使用凸松弛作为黑盒工具，我们将对基于凸松弛的方法的进一步改进作为未来的工作。

 

I　Additional Experimental Results

I.1　More results on SA-PPO

 

I.2　More results on SA-DDPG

 

I.3　Robustness Certificates

　　我们在表3中报告了SA-DQN的鲁棒性证书。如E节所述，对于DQN，我们可以保证动作在有界对抗性噪声下不会改变。在表3中，“动作认证率”是在任何l_∞范数有界噪声下不改变的动作的比率。在某些设置中，我们发现100%的动作保证不变（例如，表3中的Pong环境）。在这种情况下，我们实际上也可以证明，在特定的测试初始条件下，累积奖励没有改变。

　　在SA-DDPG中，我们可以获得鲁棒性证书，该证书在状态输入上存在有界扰动的情况下给出动作的边界。给定输入状态s，我们使用神经网络的凸松弛来获得每个动作的上下限：。我们考虑π(s)上的以下证书：平均输出范围和l₂距离。注意，在给定l_i(s)和u_i(s)的情况下，也可以计算其他l_p范数上的边界。由于动作空间被归一化为[-1, 1]，最坏情况下的输出范围为2。我们在表7中报告了所有五个环境的两个证书。没有我们的鲁棒正则化子的DDPG通常不能获得非空证书（范围接近2）。SA-DDPG可以提供鲁棒性证书（有界输入保证有界输出）。我们在E节中对这些证书进行了一些讨论。

　　对于SA-PPO，由于作用遵循高斯策略，我们可以在状态扰动下上界其KL散度。结果如表8所示。注意，通过增加正则化参数，可以以牺牲模型性能为代价获得更严格的证书。