Layer Normalization

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

Arxiv 2016

 

Abstract

　　训练最先进的深度神经网络在计算上是昂贵的。减少训练时间的一种方法是使神经元的活动归一化。最近引入的一种称为批量归一化的技术使用神经元的总输入在小批量训练案例上的分布来计算平均值和方差，然后用于在每个训练案例上归一化该神经元的总输出。这显著减少了前馈神经网络的训练时间。然而，批量归一化的效果取决于小批量大小，并且如何将其应用于循环神经网络还不明显。在本文中，我们通过计算用于归一化的均值和方差，将批量归一化转换为层归一化，该均值和方差是在单个训练情况下从一层中的所有相加输入到神经元的。像批量归一化一样，我们也给每个神经元自己的自适应偏差和增益，这些偏差和增益在归一化之后但在非线性之前应用。与批处理归一化不同，层归一化在训练和测试时执行完全相同的计算。通过在每个时间步长分别计算归一化统计量，也可以直接应用于循环神经网络。层归一化在稳定递归网络中的隐藏状态动力学方面非常有效。根据经验，我们表明，与先前发表的技术相比，层归一化可以显著减少训练时间。

 

1 Introduction

　　在计算机视觉[Krizhevsky et al.，2012]和语音处理[Hinton et al.，2012]中的各种监督学习任务上，用某种版本的随机梯度下降训练的深度神经网络已被证明显著优于以前的方法。但最先进的深度神经网络通常需要很多天的训练。通过在不同的机器上计算训练案例的不同子集的梯度，或者将神经网络本身拆分到许多机器上，可以加速学习[Dien et al.，2012]，但这可能需要大量的通信和复杂的软件。随着并行化程度的增加，它也往往会导致回报迅速减少。正交方法是修改在神经网络的前向传递中执行的计算，以使学习更容易。最近，有人提出了批量归一化[Iofe and Szegedy，2015]，通过在深度神经网络中包括额外的归一化阶段来减少训练时间。归一化使用其在训练数据上的均值和标准差来标准化每个求和的输入。使用批量归一化训练的前馈神经网络即使使用简单的SGD也能更快地收敛。除了训练时间的改进外，来自批量统计的随机性在训练过程中起到了正则化的作用。

　　尽管批量归一化很简单，但它需要对求和的输入统计数据进行平均。在具有固定深度的前馈网络中，可以直接为每个隐藏层单独存储统计信息。然而，循环神经网络（RNN）中循环神经元的总输入通常随着序列的长度而变化，因此对RNN应用批量归一化似乎需要针对不同的时间步长进行不同的统计。此外，批量归一化不能应用于在线学习任务或极小批量的超大分布式模型。

　　本文介绍了层归一化，这是一种简单的归一化方法，可以提高各种神经网络模型的训练速度。与批量归一化不同，所提出的方法直接从对隐藏层内神经元的求和输入中估计归一化统计信息，因此归一化不会在训练案例之间引入任何新的相关性。我们表明，层归一化对RNN很有效，并提高了现有几种RNN模型的训练时间和泛化性能。

 

2 Background

　　前馈神经网络是从输入模式x到输出向量y的非线性映射。考虑深度前馈神经网络中的第 l 个隐藏层，并假设a^l是该层中神经元的总输入的向量表示。通过线性投影计算求和输入，权重矩阵W^l和自下而上的输入h^l如下所示：

其中f(·)是逐元素非线性函数，是第 i 个隐藏单元的输入权重，是标量偏差参数。使用基于梯度的优化算法来学习神经网络中的参数，通过反向传播来计算梯度。

　　深度学习的挑战之一是，一层中相对于权重的梯度高度依赖于前一层中神经元的输出，特别是如果这些输出以高度相关的方式变化。批量归一化[Iofe and Szegedy，2015]被提出来减少这种不希望的“协变量偏移”。该方法对训练案例中每个隐藏单元的相加输入进行归一化。具体来说，对于第 l 层中的第 i 个求和输入，批量归一化方法根据数据分布下的方差重新缩放求和输入：

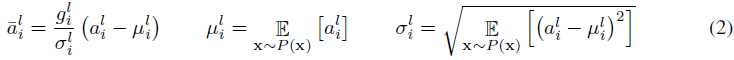
其中是到第 l 层中的第 i 个隐藏单元的归一化求和输入，g_i是在非线性激活函数之前缩放归一化激活的增益参数。请注意，期望值是在整个训练数据分布下。精确计算公式(2)中的期望值通常是不切实际的，因为这需要通过具有当前权重集的整个训练数据集进行前向传递。相反，μ和σ使用当前小批量的经验样本进行估计。这限制了小批量的大小，并且很难应用于循环神经网络。

 

3 Layer normalization

　　我们现在考虑层归一化方法，该方法旨在克服批量归一化的缺点。

　　请注意，一层输出的变化往往会导致下一层的总输入发生高度相关的变化，尤其是ReLU单元的输出可能会发生很大变化。这表明，可以通过固定每一层内求和输入的平均值和方差来减少“协变量偏移”问题。因此，我们计算同一层中所有隐藏单元的层归一化统计信息，如下所示：

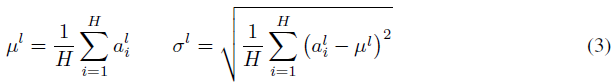
其中H表示层中隐藏单元的数量。公式(2)和公式(3)之间的区别在于，在层归一化下，层中的所有隐藏单元共享相同的归一化项，但不同的训练情况具有不同的归一化项。与批量归一化不同，层归一化不会对小批量的大小施加任何约束，并且可以在批量大小为1的纯在线状态下使用。

 

3.1 Layer normalized recurrent neural networks

　　最近的序列到序列模型[Sutskever et al.，2014]利用紧凑循环神经网络来解决自然语言处理中的序列预测问题。在NLP任务中，针对不同的训练情况具有不同的句子长度是很常见的。这在RNN中很容易处理，因为在每个时间步骤使用相同的权重。但是，当我们以显而易见的方式将批处理归一化应用于RNN时，我们需要为序列中的每个时间步骤计算和存储单独的统计信息。如果测试序列比任何训练序列都长，这是有问题的。层归一化不存在这样的问题，因为其归一化项仅取决于在当前时间步骤对层的求和输入。它也只有一组在所有时间步骤上共享的增益和偏差参数。

　　在标准RNN中，根据当前输入x^t和之前的隐藏状态向量h^t-1来计算循环层中的求和输入，计算为。层归一化的循环层使用类似于公式(3)的额外归一化项重新定中心并重新缩放其激活：

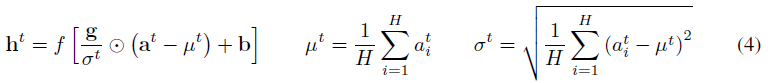
其中W_hh是循环的隐藏到隐藏权重，W_xh是自下而上的隐藏权重输入。是两个向量之间的逐元素相乘。b和g被定义为与h^t具有相同维度的偏差和增益参数。

　　在标准RNN中，循环单元的总输入的平均幅度在每个时间步骤都有增长或收缩的趋势，导致梯度爆炸或消失。在层归一化的RNN中，归一化项使其不变，可以将所有求和的输入重新缩放到一个层，这会导致更稳定的隐藏到隐藏的动力学。

 

4 Related work

　　批量归一化之前已扩展到循环神经网络[Launt et al.，2015，Amodei et al.，2015；Cooijmans et al.，2016]。先前的工作[Coijmans et al.，2016]表明，通过对每个时间步骤保持独立的归一化统计，可以获得循环批量归一化的最佳性能。作者表明，将循环批量归一化层中的增益参数初始化为0.1会对模型的最终性能产生显著影响。我们的工作也与权重归一化有关[Salimans and Kingma，2016]。在权重归一化中，使用传入权重的L2范数来归一化到神经元的求和输入，而不是方差。使用预期统计应用权重归一化或批量归一化相当于对原始前馈神经网络进行不同的参数化。在路径归一化SGD中研究了ReLU网络中的重参数化[Neyshabur et al.，2015]。然而，我们提出的层归一化方法并不是对原始神经网络的重参数化。因此，与其他方法相比，层归一化模型具有不同的不变性，我们将在下一节中进行研究。

 

5 Analysis

　　在本节中，我们研究了不同归一化方案的不变性。

 

5.1 Invariance under weights and data transformations

　　所提出的层归一化与批量归一化和权重归一化有关。尽管它们的归一化标量的计算方式不同，但这些方法可以概括为通过两个标量μ、σ和对神经元的相加输入a_i进行归一化。他们还学习了归一化后每个神经元的自适应偏差b和增益g。

请注意，对于层归一化和批量归一化，根据公式2和3计算。在权重归一化中，μ为0，并且。

　　表1强调了以下三种归一化方法的不变性结果。

Weight re-scaling and re-centering:

Data re-scaling and re-centering:

 

5.2 Geometry of parameter space during learning

 

5.2.1 Riemannian metric

 

5.2.2 The geometry of normalized generalized linear models

 

6 Experimental results

　　我们在6个任务上进行了分层归一化实验，重点是循环神经网络：图像句子排序、问答、上下文语言建模、生成建模、手写序列生成和MNIST分类。除非另有说明，否则在实验中，层归一化的默认初始化是将自适应增益设置为1，将偏差设置为0。

 

6.1 Order embeddings of images and language

 

6.2 Teaching machines to read and comprehend

 

6.3 Skip-thought vectors

 

6.4 Modeling binarized MNIST using DRAW

 

6.5 Handwriting sequence generation

 

6.6 Permutation invariant MNIST

 

6.7 Convolutional Networks

　　我们还对卷积神经网络进行了实验。在我们的初步实验中，我们观察到，在没有归一化的情况下，层归一化比基线模型提供了加速，但批量归一化优于其他方法。对于全连接层，层中的所有隐藏单元往往对最终预测做出类似的贡献，并且对层的总输入进行重新居中和重新缩放效果良好。然而，对于卷积神经网络来说，类似贡献的假设不再成立。感受野位于图像边界附近的大量隐藏单元很少被打开，因此与同一层内的其他隐藏单元具有非常不同的统计数据。我们认为需要进一步的研究才能使层归一化在卷积神经网络中发挥良好的作用。

 

7 Conclusion

　　在本文中，我们引入了层归一化来加速神经网络的训练。我们提供了一个理论分析，比较了层归一化与批归一化和权重归一化的不变性。我们证明了层归一化对于每个训练案例的特征移位和缩放是不变的。

　　经验表明，循环神经网络从所提出的方法中受益最大，尤其是对于长序列和小批量。

 

Supplementary Material

Application of layer normalization to each experiment

 

Teaching machines to read and comprehend and handwriting sequence generation

 

Order embeddings and skip-thoughts

 

Modeling binarized MNIST using DRAW

 

Learning the magnitude of incoming weights