Understanding plasticity in neural networks

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

Arxiv 2023

 

Abstract

　　可塑性是神经网络根据新信息快速改变预测的能力，对于深度强化学习系统的适应性和鲁棒性至关重要。众所周知，即使在相对简单的学习问题中，深度神经网络也会在训练过程中失去可塑性，但驱动这种现象的机制仍知之甚少。本文对可塑性损失进行了系统的实证分析，目的是从机理上理解这一现象，以指导未来有针对性的解决方案的发展。我们发现可塑性损失与损失景观曲率的变化密切相关，但它通常发生在缺乏饱和单元或发散梯度范数的情况下。基于这一见解，我们确定了许多参数化和优化设计选项，使网络能够在训练过程中更好地保持可塑性。我们通过对在Arcade学习环境中训练的深度RL智能体应用性能最佳的干预措施，即层归一化，验证了这些发现在更大规模学习问题中的实用性。

 

1. Introduction

　　人们普遍观察到，经过训练以适应一系列不同学习目标的神经网络解决新任务的能力降低（Lyle等人，2021；Nikishin等人，2022；Dohare等人，2021）。当输入和预测目标之间的关系随时间发生变化时，可塑性损失最为严重，网络必须学会“覆盖”其先前的预测（Lyle等人，2021）。虽然这种场景在监督学习中相对罕见，但它们被融入了深度强化学习（RL）智能体的训练方式中。如果我们希望开发能够不断学习解决复杂任务的深度RL智能体，了解可塑性是如何丧失的，以及这种丧失是否可以减轻，这一点至关重要。促进可训练性的现有方法作用于各种可能导致可塑性丧失的潜在机制，包括层的重置（Nikishin等人，2022）和激活单元（Dohare等人，2021），以及特征的归一化（Kumar等人，2020；Lyle等人，2021）。虽然所有这些工作都观察到了性能的改进，但它们不太可能都通过相同的机制获得这些改进。因此，很难知道如何改进这些干预措施，以进一步保持可塑性。

　　本文试图确定可塑性损失发生的机制。我们首先分析了两个可解释的案例研究，说明了自适应优化器和初始梯度下降都会导致可塑性损失的机制。先前的工作已经隐式或显式地推测，各种网络属性可能会导致可塑性损失：我们提出了一个伪造框架，该框架受到泛化因果稳健预测因子研究的启发（Dziugaite等人，2020），并利用该框架表明可塑性损失不能唯一归因于任何这些属性。虽然很难明确表征，但我们提供的证据表明，新任务对训练参数引起的损失景观的曲率是决定网络可塑性的关键因素。

　　最后，我们完成了对方法的广泛实证分析，这些方法旨在提高网络在整个训练过程中导航其优化景观的能力，从架构选择到正则化和标准化方案。我们发现，被推测为平滑损失景观的架构，例如使用分类编码和层归一化的架构，对可塑性提供了最大的改进，而扰动参数或提供其他形式的正则化的方法往往看不到什么好处。为了测试这些发现的普遍性，我们将性能最好的干预措施，即层标准化应用于标准DQN架构，并在Arcade学习环境基准测试中获得了显著的性能改进。我们的结论是，控制损失景观的清晰度和优化器的稳定性为提高深度RL方法的稳健性和可用性提供了非常有前途的途径。

 

2. Background

　　长期以来，人们一直认为，首先对网络进行一项任务的训练，然后再对第二项任务进行训练，会导致第一项任务的性能下降（French，1999）。这种现象被称为灾难性遗忘，已经被许多著作广泛研究。本文关注的是一种不同的现象：在某些情况下，在一系列不同的任务上训练神经网络，可能会导致在后续任务上的性能比训练相同架构的随机初始化网络所获得的性能更差。

 

2.1. Preliminaries

Temporal difference learning.

Loss landscape analysis.

 

2.2. Defining plasticity

　　可塑性研究已经关注神经科学几十年了（Mermillod等人，2013；Abbott&Nelson，2000），但直到最近才成为深度学习的兴趣话题（Berariu等人，2021；Ash&Adams，2020）。计算学习理论文献中关于复杂性的经典概念（Vapnik，1968；Bartlett和Mendelson，2002）评估假设类是否包含捕获任意模式的函数，但对特定搜索算法（如梯度下降）找到这些函数的能力不可知，这对它们在实际深度学习系统中的应用提出了挑战。例如，一个十亿参数的神经网络架构可能有能力表示一类丰富的函数，但如果它的所有激活单元都饱和了，那么它就不能通过梯度下降来训练来实现这种能力。为了反映这种直觉，我们将使用可塑性一词来指代与问题相关的属性，它捕捉网络状态、优化过程和训练数据之间的相互作用，而容量将指代网络架构的固定属性。

　　本工作将采用与Lyle等人（2021）类似的经验方法来定义可塑性。直观地说，我们的定义将衡量网络响应广泛的可能学习信号更新其预测的能力。我们考虑一个优化算法，它采用初始参数和一些目标函数，并输出一组新的参数θ*。参数不一定是最优的：例如，O可以运行梯度下降五步。为了衡量网络在这种优化算法下更新预测的灵活性，我们考虑了一组损失函数L上的分布，每个损失函数由一些学习目标定义。例如，我们可以考虑回归损失的分布，其中g是由神经网络的随机初始化引起的。为了与适应性更强的网络应该具有更大可塑性的直觉相匹配，我们将基线值b设置为某个基线函数获得的损失（例如，如果 l 是某组目标的回归损失，我们将b设置为目标的方差），然后将可塑性定义为在从初始参数值θ_t开始并优化采样损失函数 l，基线与通过该优化过程获得的最终损失的期望之间的差。

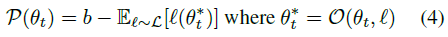
　　具体地说，我们将X设置为RL智能体收集并存储在某个回放缓冲区中的转换集，将 f 设置为神经网络架构。给定某个偏移，我们将应用变换g(x) = a + sin(10⁵f(x; θ₀))来构建一个具有挑战性的预测目标，该目标测量网络将其输入空间分解为任意分组的能力。由于随着策略的改进和奖励通过价值函数传播，深度RL网络输出的平均预测往往会随着时间的推移逐渐远离零，因此我们将a设置为等于网络的平均预测，以免使目标偏向于随机初始化，因为随机初始化的平均值更接近零。优化器O将与网络在其主要学习目标上使用的优化器相同，我们发现以两千步的预算运行该优化器可以实现合理有效的迭代时间，同时也为大多数随机初始化提供了足够的机会来解决任务。

　　在给定这个框架的情况下，我们将轨迹过程中的可塑性损失定义为差值P(θ_t) - P(θ₀)。我们注意到，可塑性损失的定义与基线b的值无关，即探测任务的难度。

 

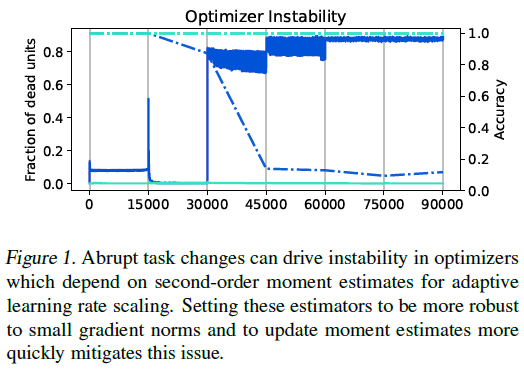
3. Two simple studies on plasticity

　　我们从一些发生可塑性损失的学习问题的可解释的例子开始。这些示例说明了优化器的设计如何与非平稳性相互作用，以产生导致可塑性损失的不稳定性，并探讨了基于梯度的优化器动态如何影响损失景观的更微妙属性。

 

3.1. Optimizer instability and non-stationarity

 

3.2. Loss landscape evolution under non-stationarity

 

4. Explaining plasticity loss

　　虽然在某些情况下，推断可塑性丧失的原因很简单，但大多数学习问题都会导致复杂的学习动力学，很难确定根本原因。本节将表明，对可塑性损失的一些合理解释，包括网络特征的秩、饱和单元的数量、其参数的范数和权重矩阵的秩，并不能确定稳健的因果关系。我们提供了一些证据来支持塑性损失是由于网络损失格局的变化而产生的假设，并讨论了在保留可训练的梯度结构和准确预测价值函数之间必须面临的潜在权衡。

 

4.1. Experimental setting

　　我们考虑的实验框架如下，将在第5节中重新讨论。我们构建了一个简单的图像分类的MDP类似物，即潜在的过渡动力学是在一组十个状态和十个动作上定义的，而奖励和过渡动力学取决于主体所采取的动作是否等于状态的潜在标签。我们构造了块MDP的三个变体，其状态空间可以由CIFAR-10或MNIST图像数据集给出。

Easy: MDP的每个状态s从底层分类数据集中的该类产生观察。给定动作a，奖励是指标函数δ_a=s。然后，MDP随机转换到一个新的状态。

Hard: 观察被分配{0 ... 9}中的随机标签，并且从具有相同随机分配标签的图像中采样来自MDP状态的观察。动力学在其他方面与easy环境相同。

Sparse: 显示出与easy相同的观测映射。奖励等于δ_a=s=9。如果a≠s，则MDP转变为随机状态，否则转变为s+1。

　　我们设计这些环境是为了满足两个主要需求：第一，它们带来了视觉上有趣的预测挑战，第二，它们允许我们隔离由于策略和目标网络更新而产生的非平稳性，而不依赖于状态访问分布的变化。在easy变体和hard变体中，过渡动力学不取决于智能体的行为，而在sparse环境中，策略影响状态访问分布。不同的奖励函数使我们能够比较符合网络归纳偏差的任务（在easy任务中）和不符合网络归纳偏差的任务（hard任务）。

　　我们在每个环境观测空间组合上训练一组DQN智能体，并评估每个网络在固定数量的训练步骤后拟合第2.2节所述的随机生成的目标函数集的能力。在这里显示的实验中，我们以1000步的目标网络更新周期运行DQN智能体；如前所述，这是“easy”和“hard”任务中非平稳性的主要来源。每走5000步，我们就暂停训练，从当前参数θ_t的副本中，我们就一组新的回归问题训练网络，以探索其可塑性。我们记录2000步优化结束时的损失，对10个不同的随机函数进行采样，然后从保存的参数θ_t恢复RL任务的训练。我们考虑两种网络架构：全连接网络（MLP）和卷积网络架构（CNN）。环境的全部细节包含在附录A.2中。

 

4.2. Falsification of prior hypotheses

　　先前的工作已经提出了一些合理的解释，解释为什么神经网络随着时间的推移可能会表现出适应新目标的能力下降。权重范数增加（Nikishin等人，2022）、特征或权重秩较低（Kumar等人，2020；Gulcehre等人，2021）和非活动特征（Lyle等人，2021；Dohare等人，2021）都被视为可能发生可塑性损失的机制。然而，这些假设的解释力还没有经过严格的检验。虽然特定变量和可塑性丧失之间的相关性可能有助于诊断，但只有因果关系表明，干预该变量必然会增加可塑性。

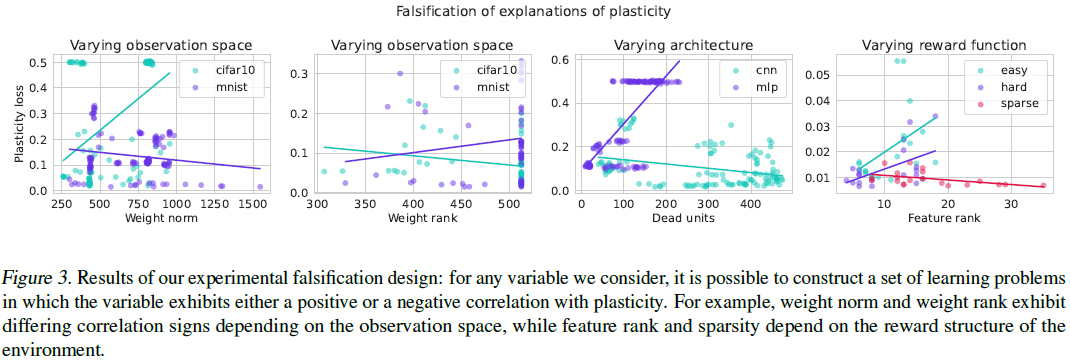
　　本节将试图回答上述候选解释是否涵盖了因果途径。我们的分析基于一个简单的前提：对于一个对可塑性损失表现出解释力的量，它应该在不同的实验干预中表现出一致的相关性（Büuhlmann，2020）。例如，如果参数范数在一个观察空间中与可塑性正相关，而在另一个观测空间中与可塑性负相关，则可以排除它是可塑性损失的原因。为了构建这个实验，我们在一系列任务、观察空间、优化器和种子下训练128个DQN智能体。在训练过程中，我们记录了参数和激活的几个统计数据，以及每个记录迭代中参数的可塑性。

　　在图3中，我们展示了散点图，说明了可塑性和每个统计数据之间的关系，其中散点图中的每个点都对应于一次训练。我们发现，对于四个量中的每一个，都存在一个学习问题，其中量与可塑性呈正相关，而其中量表现出负相关。在许多学习问题中，可塑性损失和兴趣数量之间的相关性是不存在的。在所有情况下，我们注意到每个数量与塑性之间的相关性已经很弱；即便如此，逆转这种相关性的能力是对这些简单统计数据作为可塑性因果解释的效用的进一步证明。例如，我们看到在使用CIFAR-10观测的环境中，权重标准和塑性损失之间存在正相关，但在使用MNIST观测样本的环境中存在轻微的负相关。环境中的特征等级也发生了类似的反转。

 

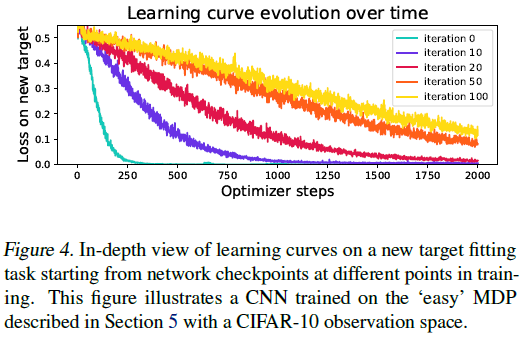
4.3. Loss landscape evolution during training

 

5. Solutions

　　到目前为止，我们已经证明，即使在像对MNIST数字进行分类这样简单的任务中，假设在优化动力学中引入一定程度的非平稳性，神经网络也可以失去可塑性。我们将注意力转向减少或扭转这种可塑性损失的方法。第5.1节将评估缩放是否足以减轻可塑性损失。第5.2节将评估各种干预措施对一系列架构可塑性的影响。我们将在第5.3节中测试这些发现对更大规模任务的适用性。

 

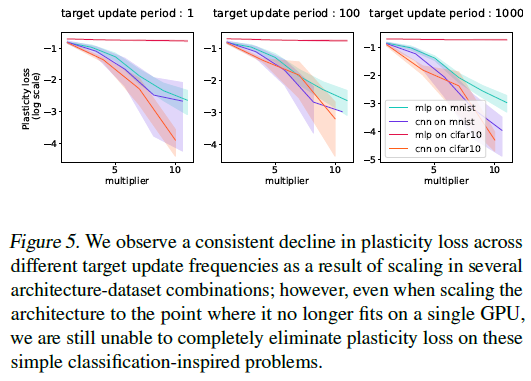
5.1. The role of scaling on plasticity

　　在考虑解决可塑性损失的复杂方法之前，我们必须首先回答这样一个问题，即这是否只是小型网络的一种疾病。在大型模型取得令人印象深刻的成功和由此产生的“比例定律”现象的背景下（Kaplan et al.，2020），可塑性损失和许多其他挑战一样，在无限计算的极限下消失是完全合理的。我们发现，虽然在小型网络中，可塑性损失最容易以极端形式诱发，但将CNN扩展到单个GPU内存的极限，即使在上一节中描述的简单分类任务中，也不足以消除可塑性损失。我们在图5中可视化了网络宽度和可塑性损失之间的关系。

　　这些观察结果表明，可塑性损失不太可能成为足够大的网络在足够简单的任务中的限制因素。然而，对于与网络的归纳偏差不一致的任务，或者网络没有足够的表达能力的任务，我们看到即使在更大的架构中，适应新目标的能力也会降低。由于我们通常无法先验地保证学习问题将属于第一类，因此我们将注意力转向其他设计选择，这些选择可能会进一步确保网络不受可塑性损失的影响。

 

5.2. Interventions in toy problems

　　在本节中，我们评估了各种干预措施对可塑性丧失的影响。我们评估了第4.1节中使用的相同任务的干预措施，即1000步的100次迭代训练。我们考虑了四种架构：多层感知器（MLP）、无跳过连接的卷积神经网络（CNN）、ResNet-18（He et al.，2016）和基于ViT架构的小型转换器（Dosovitskiy et al.，2020）。

　　我们考虑以下干预措施：在每次目标网络更新时重置网络的最后一层，这是Nikishin等人(2022)提出的方案的简化变体; 在每次目标网络更新时重置所述网络优化器状态；在CNN和MLP的每个卷积和全连接层之后添加层归一化（Ba et al.，2016）；执行收缩和扰动（Ash & Adams，2020）：将网络权重乘以一个小标量，并添加一个等于随机初始化网络权重的扰动；CNN和MLP初始线性层的光谱归一化（Gogianu et al.，2021）；和权重衰减，将l2惩罚系数设置为10^-5。

　　这些方法被选为减轻可塑性损失的多种方法的代表性样本：重置优化器状态和最后一层，暂时从优化过程中消除不良条件的来源；层归一化和残差连接往往使网络对优化器的选择更加鲁棒；权重衰减和谱归一化都以不同的方式正则化网络的参数；收缩和扰动在不显著改变决策边界的情况下对当前参数应用扰动（尽管我们注意到，对于回归任务，这仍然会影响网络输出的规模，因此可能不合适）。

　　我们在图6中看到了我们的关键收获，图6比较了在每种架构干预组合上进行100次迭代训练后的可塑性损失。总的来说，在我们考虑过的所有方法中，明确构建一个平滑损失景观的网络参数化是保持可塑性的最有效手段，并且对可塑性的影响比重置网络的最后一层更大。我们在补充材料中的图16中可视化了具有和不具有层归一化的网络的一些学习曲线。

　　我们注意到，虽然两种热编码确实显著降低了可塑性损失，但在我们考虑的几个例子中，它是以学习策略的稳定性为代价的。此外，这种干预需要与回归参数化显著不同的优化器超参数，这表明尽管它可以是稳定优化的强大工具，但它可能不适合作为插件解决方案来缓解现有协议中的可塑性损失。

 

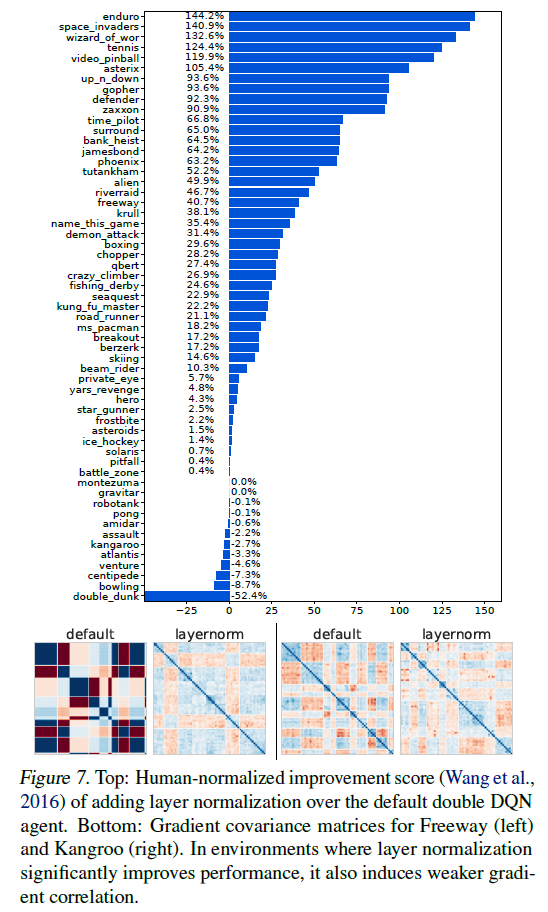
5.3. Application to larger benchmarks

　　我们现在评估了试验性分类任务中层标准化对可塑性的好处是否转化为更大的基准。我们使用Quan & Ostrovski（2020）提供的DDQN的标准实现（Van Hasselt et al.，2016），并在Arcade学习环境基准（Bellemare et al.，2013）中对57款游戏中的每一款的三个种子进行评估。我们使用RMSProp优化器、贪婪探索和帧堆叠（Mnih et al.，2015）。完整的实现细节见附录A.3。基线实现和我们的修改之间的唯一区别是在网络中的每个隐藏层之后加入了层标准化。

　　我们在图7中看到，层归一化的引入有力地提高了整个基准测试的性能。我们强调，我们没有执行任何优化器或其他超参数调整。虽然这种改进不能完全归因于所提供的证据中塑性损失的减少，但它指出优化景观的正则化是朝着更稳健的RL智能体方向发展的一个富有成效的方向。我们进一步观察到，层归一化显著提高性能的许多环境是默认架构的梯度协方差结构退化或Hessian病态的环境，并且获得性能改进的LN网络往往具有相应更好的梯度和Hessian结构。我们在图7中对这一现象进行了提示，并将对所有57个游戏的完整评估推迟到附录B.3中。

 

6. Related Work

 

7. Conclusions

　　本文的研究结果突出了课程学习和基础模型的研究之间的分歧，基础模型确定了合适的早期训练目标，以加速学习并提高后期任务的泛化能力，而我们已经发现的关于非平稳预测问题中可塑性损失的现象。然而，随着强化学习算法扩展到更复杂的任务，这些机制之间的差距缩小了。虽然在许多情况下，可塑性损失可能不是网络性能的限制因素，因此对于今天用于基准测试算法的许多相对较小的环境来说不必担心，但我们推测，随着我们应用RL的任务的复杂性的增加，保持可塑性的重要性也会增加。

　　本文的研究结果表明，稳定损失格局是促进可塑性的关键一步。这种方法可能有许多附带的好处，为未来的研究提供了一个令人兴奋的方向。更平滑的损失景观既更容易优化，也已被经验观察到表现出更好的泛化能力，更好地理清记忆和泛化在可塑性中的互补作用是未来工作的一个令人兴奋的方向。

 

A. Experiment details

A.1. Case studies

Optimizer instability:

Brownian motion:

 

A.2. Toy RL environments

 

A.3. Double DQN

　　我们遵循Atari的标准训练协议，训练2亿帧，并每4个环境步骤执行一次优化器更新（Quan & Ostrovski，2020）。我们在网络的每个隐藏层之后添加层归一化。我们使用大小为100000的重放缓冲区，并在训练期间使用ε-贪婪策略（ε=0.1）。

 

B. Additional analysis

B.1. Detailed intervention analysis

 

B.2. Learning curves for classification MDPs

B.2.1. TRAINING ACCURACY

 

B.2.2. PROBE TASKS

 

B.3. Qualitative findings in DDQN