Muesli: Combining Improvements in Policy Optimization

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

ICML 2021: 4214-4226

 

Abstract

　　我们提出了一种新的策略更新，将正则化策略优化与模型学习相结合，作为辅助损失。这一更新（此后称为Muesli）与MuZero在Atari上的最先进性能相匹配。值得注意的是，Muesli在不使用深度搜索的情况下做到了这一点：它直接与策略网络交互，计算速度与无模型基准相当。Atari的结果得到了广泛的消融，以及连续控制和9x9围棋的额外结果的补充。

 

1. Introduction

　　强化学习（RL）是不确定性条件下顺序决策问题的一般表述，其中学习系统（智能体）必须学习从与环境交互的经验中最大化其嵌入的世界（环境）提供的累积回报（Sutton&Barto，2018）。如果一个智能体的行为，即其策略，是从学到的价值估计中推断出来的（例如通过检查），则该智能体被称为基于价值的（Sutton，1988；Watkins，1989；Rummery&Niranjan，1994；Tesauro，1995）。相反，基于策略的智能体根据过去的经验直接更新（参数化）策略（Williams，1992；Sutton等人，2000）。我们还可以将直接根据经验更新价值和策略的智能体归类为无模型智能体（Sutton，1988），将使用（学到的）模型以规划全局（Sutton等人，1990）或本地（Richalet等人，1978；Kaelbling&Lozano-Pérez，2010；Silver&Veness，2010）价值和策略的智能体归类于基于模型的智能体（Oh等人，2015；van Hasselt等人，2019）。这样的区别对于沟通很有用，但是，为了掌握在环境中优化奖励的单一目标，智能体通常会结合来自不止一个领域的想法（Hessel等人，2018；Silver等人，2016；Schrittwiser等人，2020）。

　　在本文中，我们关注RL的一个关键部分，即策略优化。我们将问题的精确表述留待以后讨论，但不同的策略优化算法可以被视为以下关键问题的答案：

　　给定智能体与世界交互的数据，以及价值函数或模型形式的预测，我们应该如何更新智能体的策略？

　　我们从分析总体策略优化的需求出发。其中包括支持部分可观测性和函数逼近，学习随机策略的能力，对不同环境或训练机制（例如异策数据）的鲁棒性，以及能够将知识表示为价值函数和模型。请参阅第3节，了解有关策略优化需求的更多详细信息。

　　然后，我们提出了一种将规则化策略优化与基于模型的思想相结合的策略更新，以便在需求中强调的维度上取得进展。更具体地说，我们使用受MuZero启发的模型（Schrittwiser等人，2020），通过一步前瞻（one-step look-ahead）来估计动作价值。然后将这些动作价值插入到修改后的最大后验策略优化（Maximum a Posteriori Policy Optimization，MPO）（Abdolmaleki等人，2018）机制中，该机制基于裁剪的归一化优势，对缩放问题具有鲁棒性，而不需要约束优化。然后，名为Muesli的总体更新将裁剪的MPO目标和策略梯度组合成一种直接方法（Vieillard等人，2020），用于规则化策略优化。

　　我们的大部分实验是在Arcade Learning Environment（Bellemare等人，2013；Machado等人，2018）的57款经典Atari游戏上进行的，这是深度RL的流行基准。我们发现，在Atari上，Muesli可以与MuZero的最先进性能相匹配，而不需要深入搜索。Muesli直接与策略网络合作，在更新中使用一步前瞻。为了帮助理解Muesli的不同设计选择，我们在Atari上的实验包括对我们提出的更新进行多次消融。此外，为了评估我们的方法在不同领域的推广效果，我们在一套连续控制环境（基于MuJoCo，来源于OpenAI Gym（Brockman等人，2016））上进行了实验。我们还在9x9围棋中进行了自我游戏实验，以评估我们在传统上由搜索方法主导的领域中的策略更新。

 

2. Background

The environment. 我们感兴趣的是具有可变回合长度的回合式环境（例如Atari游戏），形式化为具有初始状态分布μ和折扣γ∈[0,1)的马尔可夫决策过程（MDPs）；回合结束对应于没有奖励的吸收状态。

 

3. Desiderata and motivating principles

　　首先，为了激励我们的研究，我们讨论了通用策略优化算法的一些需求。

 

3.1. Observability and function approximation

　　能够学习随机策略，并能够利用蒙特卡洛或多步引导回报估计，这对于策略更新真正具有普遍性非常重要。

　　这是由于在部分可观察环境（Åström，1965）中学习的挑战，或者更一般地，在使用函数近似的环境中学习（Sutton&Barto，2018）。请注意，这两者密切相关：如果选定的函数近似忽略了状态特征，则出于所有实际目的，状态特征是不可观察的。

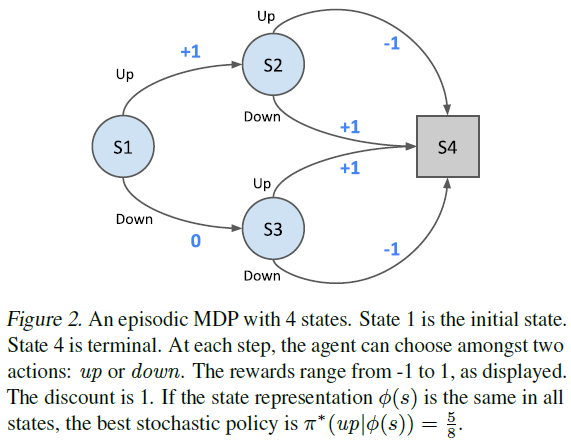
　　如Singh等人（1994）所示，在POMDP中，最优无内存随机策略可能优于任何无内存确定性策略。作为示例，考虑图2中的MDP；在这个问题中，我们有4个状态，每个步骤有2个动作（向上或向下）。如果所有状态的状态表示相同，最优策略是随机的。我们可以很容易地用笔和纸找到这样的策略：；详见附录B。

　　众所周知，在这些情况下，通常最好利用蒙特卡洛回报，或至少多步自举估值器，而不是使用一步目标（Jaakkola等人，1994）。再次考虑图2中的MDP：的自举产生了预期回报的偏差估计，因为聚集了多个状态的价值；同样，关于推导，请参见附录B。

　　在第2节中的方法中，策略梯度和MPO都允许收敛到随机策略，但只有策略梯度自然地包含多步回报估计。在MPO中，随机回报估计可能会使智能体过于乐观。

 

3.2. Policy representation

　　策略可以由动作价值构建，或者它们可以组合动作价值和其他量（例如，策略或历史数据的直接参数化）。我们认为仅靠动作价值是不够的。

　　首先，我们表明动作价值并不总是足以代表最佳随机策略。再次考虑图2中的MDP，在所有状态中都有相同的状态表示。如所讨论的，最优随机策略为。这种不一致的策略不能从Q值中推断出来，因为这些值对于所有动作都是相同的，因此对于最佳概率完全没有信息：。同样，如果没有策略，模型本身也是不够的，因为它会产生同样的无信息的动作价值。

 

3.3. Robust learning

　　我们寻求对1）异策或历史数据具有鲁棒性的算法；2） 值和模型不准确；3） 环境的多样性。在下面的段落中，我们将讨论每一个都需要什么。

　　重复使用策略π之前迭代的数据（Lin，1992；Riedmiller，2005；Mnih等人，2015）可以使RL更加高效。然而，如果在来自旧策略π_prior的数据上计算目标的梯度，则梯度的非规则应用会降低π的值。退化的数量取决于π和π_prior的总变化距离，我们可以使用正则化器来控制它，如保守策略迭代（Kakade&Langford，2002）、信任区域策略优化（Schulman等人，2015）和附录C。

　　无论我们是否了解策略，智能体的预测都包含了错误。正则化在这里也有帮助。例如，如果Q值有误差，MPO正则化器保持强大的性能界限（Vieillard等人，2020）。多次迭代的误差取平均值，而不是出现在绝对误差的折扣和中。虽然并非该结果背后的所有假设都适用于近似设置，但第5节显示，MPO类正则化器在经验上是有用的。

 

3.4. Rich representation of knowledge

　　即使策略被明确参数化，我们也认为智能体以多种方式表示知识（Degris&Modayil，2012）以可靠和稳健的方式更新此类策略是很重要的。有两类预测被证明特别有用：价值函数和模型。

　　价值函数（Sutton，1988；Sutton等人，2011）可以捕获长期累积量的知识，但能够以独立于预测跨度的成本进行学习（van Hasselt&Sutton，2015）。它们已广泛用于策略优化，例如，实现各种形式的方程减少（Williams，1992），并允许通过自举在线更新策略，而无需等待事件完全解决（Sutton等人，2000）。

　　模型也可以在各种方面发挥作用：1）学习模型可以作为辅助任务（Schmidhuber，1990；Sutton等人，2011；Jaderberg等人，2017；Guez等人，2020），并有助于表征学习；2） 学到的模型可用于通过规划更新策略和价值（Werbos，1987；Sutton，1990；Ha&Schmidhuber，2018）；3） 最后，该模型可用于规划动作选择（Richalet等人，1978；Silver&Veness，2010）。学到的模型的这些好处与MuZero纠缠在一起。有时，将它们解耦可能是有用的，例如，保留表征学习和策略优化模型的好处，而不依赖于动作选择规划的计算密集过程。

 

4. Robust yet simple policy optimization

　　表1列出了所有需求。这些问题远未解决，但它们有助于解释策略更新。在本节中，我们将描述一种旨在解决这些需求的策略优化算法。

 

4.1. Our proposed clipped MPO (CMPO) regularizer

　　我们使用最大后验策略优化（MPO）算法（Abdolmaleki等人，2018）作为起点，因为它可以学习随机策略（1a），支持离散和连续的动作空间（2c），可以从异策数据中稳定地学习（3a），甚至在使用近似Q值时也具有很强的性能界限（3b）。然后，我们提高了MPO对π和π_prior之间的总变化距离的控制程度（3a），避免了敏感的域特定超参数（3d）。

　　MPO使用正则化器Ω(π) = λKL(π, π_prior)，其中π_prior是先前的策略。由于我们对从陈旧数据中学习感兴趣，我们允许π_prior对应于任意的先前策略，并且我们基于新目标引入正则化器Ω(π) = λKL(π_CMPO, π)：

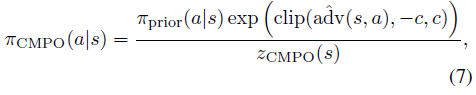
其中是优势的非随机近似，因子z_CMPO(s)确保策略是有效的概率分布。我们在正则化器中使用的CMPO项与自然策略梯度有一个有趣的关系（Kakade，2001）：如果相对于π_prior的logits计算自然梯度，然后裁剪期望的梯度，则获得π_CMPO（为了证明，相对于logits的自然策略梯度等于优势（Agarwal等人，2019））。

　　裁剪阈值c控制π_CMPO和π_prior之间的最大总变化距离。具体而言，π'和π之间的总变化距离定义为：

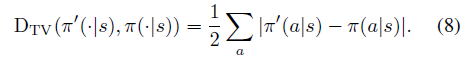
　　如第3.3节所述，受约束的总变化支持稳健的异策学习。被剪裁的优势使我们不仅可以导出总变化距离的界限，而且可以导出精确的公式：

Theorem 4.1 (Maximum CMPO total variation distance)

　　对于任何裁剪阈值c>0，我们有：

 

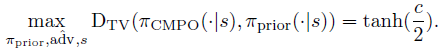
　　关于定理4.1的证明，请参见附录D；我们还对定理预测进行了数值验证。

　　请注意，π_CMPO和π_prior之间的最大总变化距离并不取决于操作数或其他环境属性（3d）。它只取决于如图3a所示的裁剪阈值。这允许在CMPO更新下控制最大总变化距离，例如通过将最大总变化距设置为ε，而不需要原始MPO论文中使用的约束优化程序。我们只设置c=2 arctanh(ε)，而不是约束优化。我们在所有领域的实验中使用了c=1。

 

4.2. A novel policy update

 

4.3. Learning a model

 

4.4. Using the model

 

4.5. Normalization

 

5. An empirical study

 

6. Conclusion